欢迎! 如果你想要学习 Dijkstra 算法,这篇文章正是为你准备的。你可以通过逐步的图文解释来理解它背后的工作原理。
你将学到:
- 图的基本概念。
- Dijkstra 算法的使用场景。
- Dijkstra 算法的工作原理。
开始吧。✨
🔹 “图”简介
基本概念
图是一种用来表示元素对之间的“连接”的数据结构。
- 这些元素称为节点,它们表示现实生活中的对象、人或实体。
- 节点之间的连接称为边。
下面是“图”的图形表示:
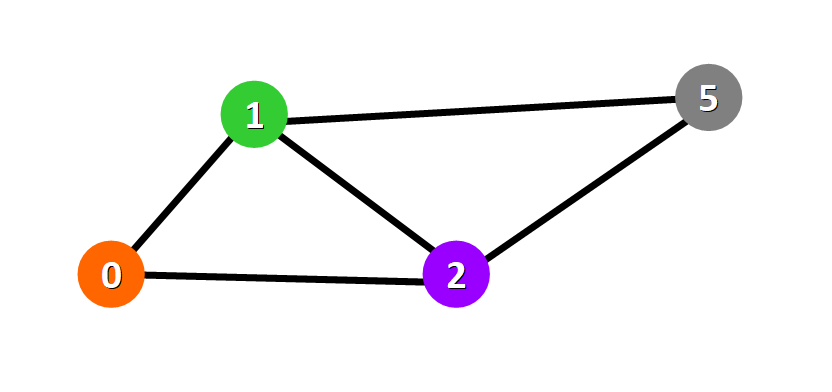
彩色的圆圈表示节点,圆圈之间的连线表示边。
💡 提示: 如果两个节点之间有连线表示它们是互相连接的。
应用
图可以应用到现实世界中的场景,例如:可以用来建模交通运输网络,节点表示发送或接收物资的站点,边表示站点之间的路线(如下图所示)。
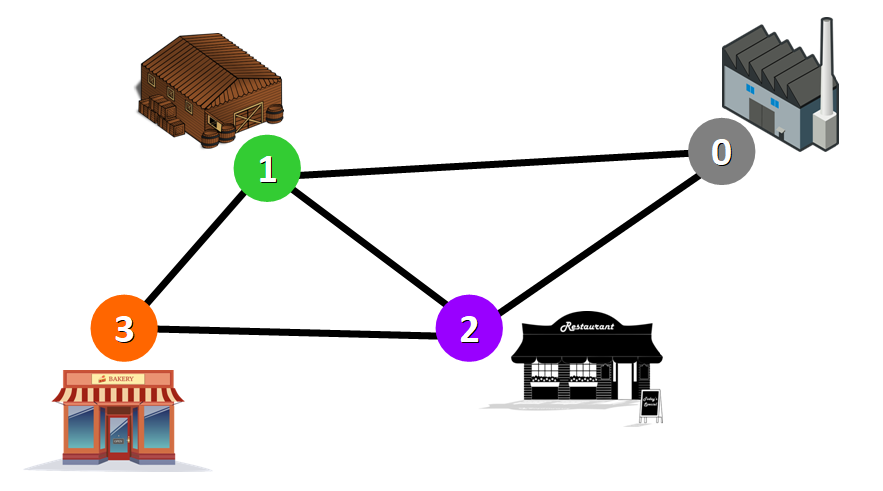
用图表示交通运输网络
图的类型
图可以是:
- 无向的: 在互相连接的节点之间可以以任意方向移动。
- 有向的: 在互相连接的节点之间只能以特定的方向移动。使用带单向箭头的线来表示有向边。

💡 提示: 本文中使用的是无向图
权重图
权重图的边是带有“权重”的,边的权重可以表示距离、时间或其他能够以节点之间的“连接”表示的概念。
下面的权重图中,每个边旁边都有一个蓝色数字表示其权重。
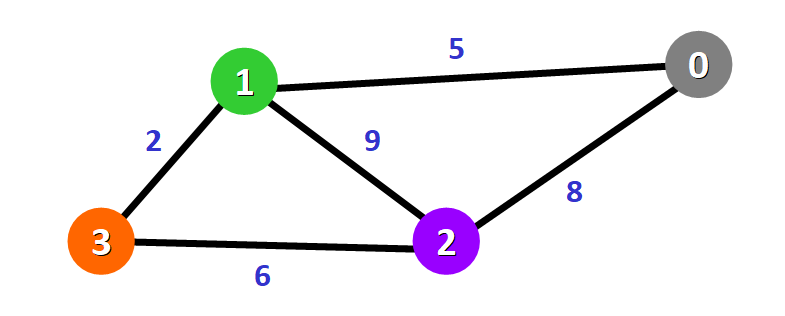
💡 提示: 这些权重对于 Dijkstra 算法而言是必不可少的,稍后会解释其原因。
🔸 Dijkstra 算法简介
了解了图的基本概念,我们开始研究这个出色的算法。
- 算法目标和使用场景
- 历史
- 基础知识
- 必要条件
算法目标和使用场景
使用 Dijkstra 算法,可以寻找图中节点之间的最短路径。特别是,可以在图中寻找一个节点(称为“源节点”)到所有其它节点的最短路径,生成一个最短路径树。
GPS 设备使用这个算法来寻找当前位置到目标位置的最短路径。Dijkstra 算法被广泛应用在工业上,尤其是需要建模网络的领域。
历史
荷兰杰出计算机科学家、软件工程师 Dr. Edsger W. Dijkstra 创建并发布了这个算法。
1959 年,他发表了一篇 3 页的文章《A note on two problems in connexion with graphs》来介绍他的新算法。

1994 年,Edsger Dijkstra 博士 在 ETH Zurich(Andreas F. Borchert 摄)
在 2001 年的一次采访中,Dijkstra 博士透露了他设计这个算法的起因和过程:
从 Rotterdam 到 Groningen 的最短路线是什么?我花了大概 20 分钟时间设计了这个寻找最短路径的算法。一天早上我正和我年轻的未婚妻在 Amsterdam 逛街,觉得有点累了,我们就坐在咖啡厅的露台上喝了一杯咖啡,我在想是否能够解决这个问题,然后,我设计出了这个最短路径算法。我说过,这是一个 20 分钟的设计。事实上,三年之后的 1959 年它才被发布,现在看来依然很不错,其原因之一是我当时设计的时候没有纸和笔,从而不得不极力避免所有可避免的复杂性。最终,令我惊讶的是,这个算法成为了我成名的基石之一。——引自文章《An interview with Edsger W. Dijkstra》.
⭐ 难以置信,对吧? 仅仅 20 分钟的时间,Dijkstra 博士设计出了位列计算机科学史上最著名的算法之一的 Dijkstra 算法。
Dijkstra 算法的基础知识
- Dijkstra 算法从指定的节点(源节点)出发,寻找它与图中所有其它节点之间的最短路径。
- Dijkstra 算法会记录当前已知的最短路径,并在寻找到更短的路径时更新。
- 一旦找到源节点与其他节点之间的最短路径,那个节点会被标记为“已访问”并添加到路径中。
- 重复寻找过程,直到图中所有节点都已经添加到路径中。这样,就可以得到从源节点出发访问所有其他节点的最短路径方案。
必要条件
Dijkstra 只能用在权重为正的图中,因为计算过程中需要将边的权重相加来寻找最短路径。
如果图中有负权重的边,这个算法就无法正常工作。一旦一个节点被标记为“已访问”,当前访问它的路径就被标记为访问它的最短路径。如果存在负权重,则可能在之后的计算中得到总权重更小的路径,从而影响之前的结果(译注:即可能出现多绕路反而路线更短的情况,不合实际)。
🔹 Dijkstra 算法示例
理解了算法概念之后,通过逐步的示例来了解一下它背后的工作原理。
假设有下面这个图:
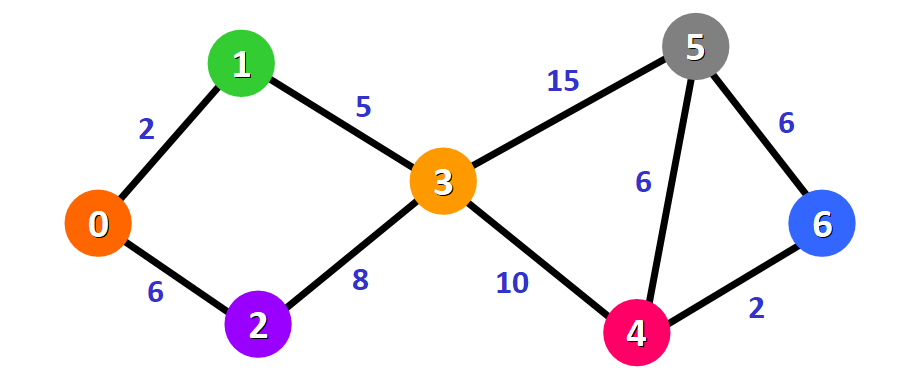
Dijkstra 算法将会寻找出图中节点 0 到所有其他节点的最短路径。
💡 提示: 在这个图中,我们假定两个节点之间的权重表示它们之间的距离。
我们将会得到节点 0 到节点 1、节点 0 到节点 2、节点 0 到 节点 3……(以此类推)的最短路径。
初始的距离列表如下:
- 源节点到它自身的距离为
0。示例中的源节点定为节点0,不过你也可以选择任意其它节点作为源节点。 - 源节点到其它节点的距离还没有确定,所以先标记为无穷大。

还有一个列表用来记录哪些节点未被访问(即尚未被包含在路径中):

💡 提示: 记住,当所有节点都被添加到路径中时,算法的计算过程就完成了。
我们选择了从节点 0 出发,可以直接将它标记为“已访问”,同样的,在未访问节点列表中把它划掉,并在图中给它加上红色的边框:

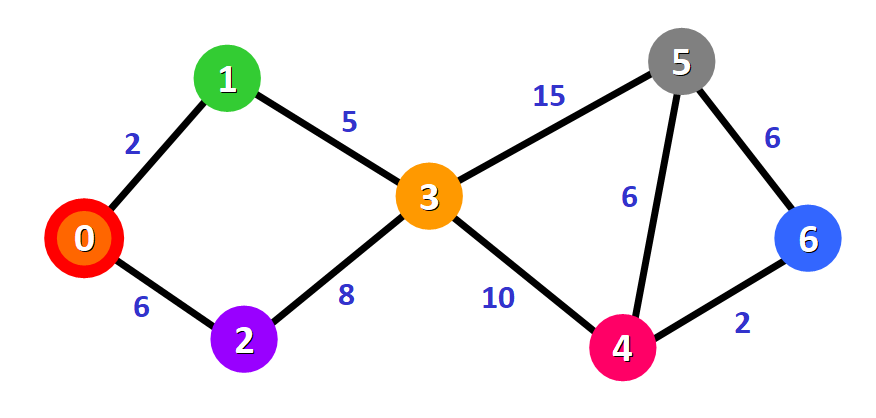
现在需要检查节点 0 到相邻节点的距离,两个相邻节点分别是节点 1 和节点 2(注意看红色的边):
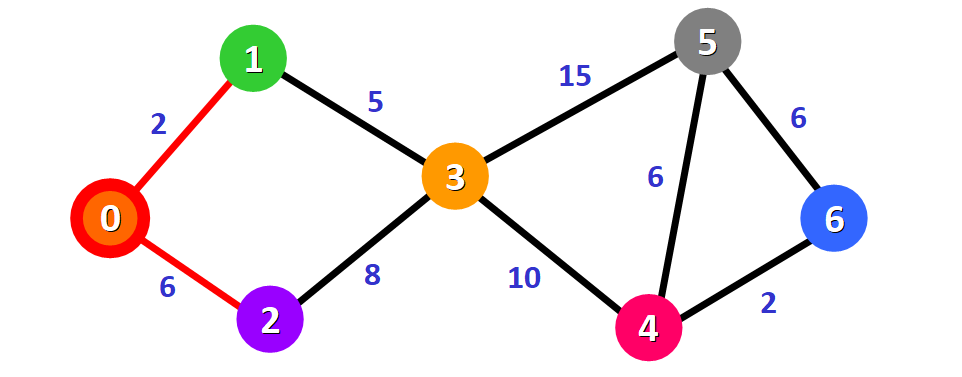
💡 提示: 这并不是说立即把这两个相邻节点加入到最短路径中。在把一个节点加入到最短路径之前,需要确认是否已经寻找到了访问它的最短路径。现在只是在对可选方案做初步检查。
更新节点 0 到节点 1、节点 0 到节点 2 的距离为它们之间的边的权重,分别为 2 和 6:

更新了到相邻节点的距离之后:
- 根据已知的距离列表选择距离源节点最近的节点。
- 将它标记为“已访问”。
- 将它添加到路径中。
查看距离列表,发现节点 1 到源节点的距离是最短的(距离为 2),所以把它加入到路径中。
在图中,以红色边来表示:
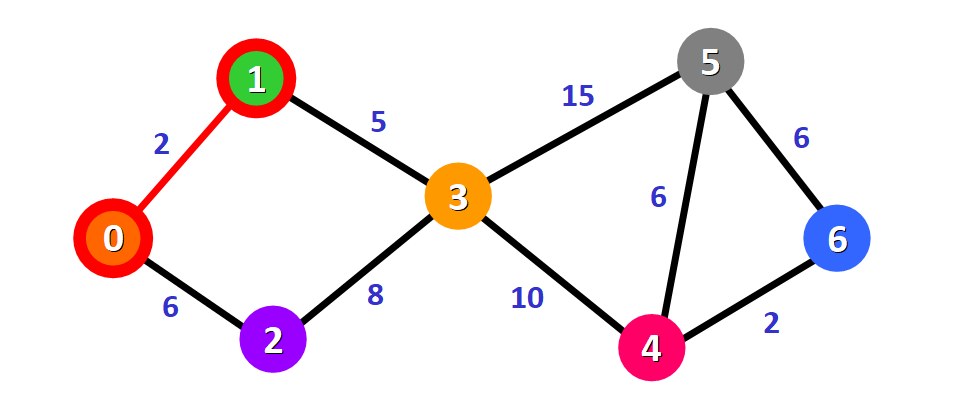
在距离列表中用红色方块标记这个节点,表明它是“已访问”的、已经寻找到了访问这个节点的最短路径:

在未访问节点列表中将它划掉:

现在分析新的相邻节点,寻找访问它们的最短路径。只需要分析已经在最短路径(标记为红色边)中的节点的相邻节点。
节点 2 和节点 3 都是最短路径包含的节点的相邻节点,因为它们分别与节点 0 和节点 1 直接相连,如下图所示。下一步将要分析这两个节点。

之前已经计算过源节点到节点 2 的距离,并记录在了列表中,所以不用更新。这次只需要更新源节点到新的相邻节点(节点 3)的距离:

这个距离是 7,来看看为什么。
为了计算源节点到另一个节点(这里指节点 3)的距离,需要把访问该节点的最短路径的所有边权重相加:
- 对于节点
3: 将构成路径0 -> 1 -> 3的所有边权重相加,得到总距离为 7(0 -> 1距离为 2,1 -> 3距离为 5)。

现在得到了到相邻节点的距离,需要选择一个节点添加到路径中。我们必须选择一个已知到源节点距离最短的未访问节点。
从距离列表中可以看出,距离为 6 的节点 2 就是我们的选择:

在图中为它加上红色边框,并将路径上的边标记为红色:

在距离列表中用红色方块把它标记为“已访问”,在“未访问”节点列表中把它划掉:


重复前面的步骤,寻找源节点到新的相邻节点节点 3 的最短路径。
可以看到,有两种可选的路径:0 -> 1 -> 3 或 0 -> 2 -> 3。一起看看我们是如何确定最短路径的。

节点 3 在之前已经有了一个距离记录(距离为 7,参阅下表),这个距离是之前步骤中由路径 0 -> 1 -> 3 的两个边权重(分别为 5 和 2)相加得到的。
不过现在有了一个新的可选路径:0 -> 2 -> 3,它途经权重分别为 6 和 8 的两条边 0 -> 2 和 2 -> 3,总距离为 14。

显然,第一个路径的距离更短(7 vs. 14),所以选择第一个路径 0 -> 1 -> 3。只有在新的路径距离更短的情况下,才会更新距离列表。
因此,使用第一种方案 0 -> 1 -> 3,将节点添加到路径中。

把这个节点标记为“已访问”,在“未访问”节点列表中把它划掉:


重复前面的过程。
检查尚未访问的相邻节点:节点 4 和节点 5,因为它们是节点 3 的相邻节点。

更新它们到源节点的距离,尝试寻找更短的路径:
- 对于节点
4: 路径是0 -> 1 -> 3 -> 4,距离为 17。 - 对于节点
5: 路径是0 -> 1 -> 3 -> 5,距离为 22。
💡 提示: 注意我们只能从最短路径(红色边)上进行扩展,而不能途经未被包含在最短路径中的边(例如,不能构造经过边 2 -> 3 的路径)。

现在需要选择将哪个未访问节点标记为“已访问”,这里选择节点 4,因为在距离列表中它的距离最短。在图中做标记:
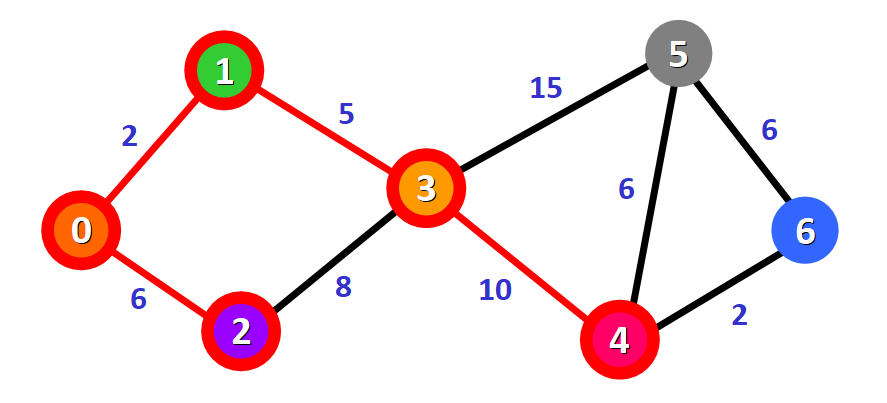
在距离列表中用红色方块将它标记为“已访问”:
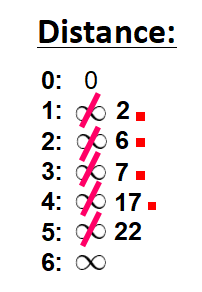
在“未访问”节点列表中把它划掉:

再次重复前面的过程。检查相邻节点:节点 5 和节点 6。分析每一种从已访问节点到它们之间的可能路径方案。

对于节点 5:
- 第一种选择是路径
0 -> 1 -> 3 -> 5,到源节点的距离为 22(2 + 5 + 15),前面的步骤已经记录了这个距离。 - 第二种选择是路径
0 -> 1 -> 3 -> 4 -> 5,到源节点的距离为 23(2 + 5 + 10 + 6)。
显然,第一个路径距离更短,为节点 5 选择第一种方案。
对于节点 6:
- 可选的路径是
0 -> 1 -> 3 -> 4 -> 6,到源节点的距离为 19(2 + 5 + 10 + 2)。

把距离最短(当前已知)的节点 6 标记为“已访问”。

在“未访问”节点列表中把它划掉:

现在得到了如下路径(标记为红色):

现在只剩下一个节点 5 还没被访问了,看看我们要如何把它添加到路径中。
从已经添加到路径中的节点出发,有三种不同的路径可以访问节点 5:
- 第一种选择:
0 -> 1 -> 3 -> 5,总距离为 22(2 + 5 + 15)。 - 第二种选择:
0 -> 1 -> 3 -> 4 -> 5,总距离为 23(2 + 5 + 10 + 6)。 - 第三种选择:
0 -> 1 -> 3 -> 4 -> 6 -> 5,总距离为 25(2 + 5 + 10 + 2 + 6)。

选择总距离为 22 的最短路径:0 -> 1 -> 3 -> 5。
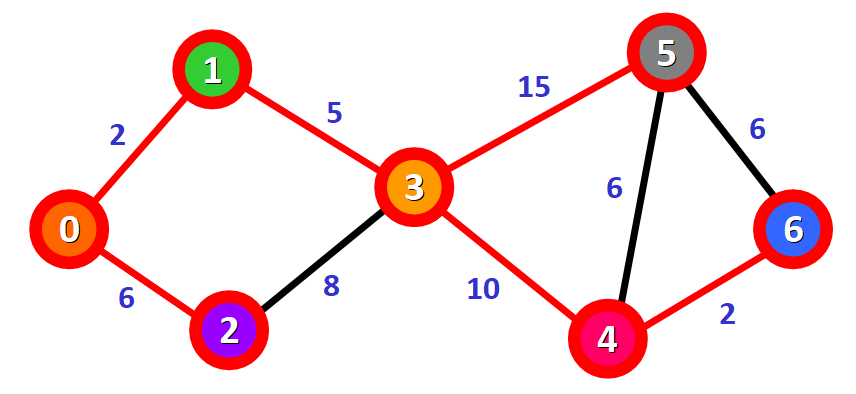
把这个节点标记为“已访问”,并在“未访问”节点列表中把它划掉:


瞧! 我们得到了从节点 0 到图中每个节点的最短路径。

图中,标记为红色的边表示最短路径:连接节点 0 和目标节点的红色边即为从源节点出发访问目标节点的最短路径。
例如,想要从节点 0 出发访问节点 6,连接它们的红色边就是最短路径,跟着走就行了。
🔸 总结
- 图可以用来建模对象、人或实体之间的连接。它有两个关键要素:节点和边,节点表示对象,边表示对象之间的连接。
- Dijkstra 算法能够寻找出图中指定节点(“源节点”)到所有其他节点的最短路径。
- Dijkstra 算法利用边的权重来做计算,寻找源节点到所有其他节点的总距离最短(总权重最小)的路径。
希望你喜欢我的文章并且有所收获。 想必你现在已经理解了 Dijkstra 算法背后的工作原理了。欢迎关注我的 Twitter @EstefaniaCassN 或查看我的在线课程。
原文:Dijkstra's Shortest Path Algorithm - A Detailed and Visual Introduction,作者:Estefania Cassingena Navone

