原文: How to Build an AI for Two-Player Turn-based Games
双人回合制游戏是指两个玩家对弈,多个回合,直到其中一人获胜。这类游戏的例子有井字游戏、西洋双陆棋、曼卡拉、国际象棋和 Connect 4 四子棋。
在本教程中,我们将学习 Minimax 算法。它是一种用于决策和博弈论的回溯算法。它为棋手找到最优棋步,假设他们的对手也以最优方式下棋。它被广泛用于双人回合制游戏中。
你将学会如何创建自己的人工智能,玩上述任何游戏或其他类似游戏。另外,为了尽可能使其容易理解,我将把该算法应用于 Tic-Tac-Toe 井字游戏。
我们将不涉及创建游戏的整个过程,而只涉及与人工智能有关的部分,因为这是我们的主题。如果你对游戏创建过程感兴趣,你可以在 GitHub 上查看这个使用人工智能的井字游戏及其源代码。这是我很久以前做的一个项目,它仍然是我的最爱之一。
目录
- Minimax 算法是如何运行的
- Minimax 算法的局限性
- 如何提高该算法的时间复杂度
- 井字游戏 AI 代码
- 总结
Minimax 算法是如何运行的
Minimax 算法的方法非常简单。首先,它从一个给定的位置检查所有可能的组合。然后,假设双方都发挥得很好,它就会选择使获胜机会最大化的最佳棋步。
为了说明这一点,让我们考虑一个井字游戏,使之更有说服力。正如你可能知道的,在这个游戏中,有 2 个玩家和 9 个空位。所以我们可以用一个长度为 9 的数组来表示一个游戏。
现在让我们以这个棋盘为例:正如你所看到的,一个游戏棋盘是一个长度为 9 的数组,其值可以是 X、O 或空字符串。一个空字符串意味着这个位置仍然可用。

现在轮到 X 了。Minimax 算法将从这个位置开始尝试所有的游戏组合。然后,它将从所产生的子位置尝试所有的游戏组合,直到达到一个位置,游戏结束时,要么是 X 赢,要么是 O 赢,要么是平局(当棋盘满了,没有人赢)。
这张图说明了这是如何运行的:
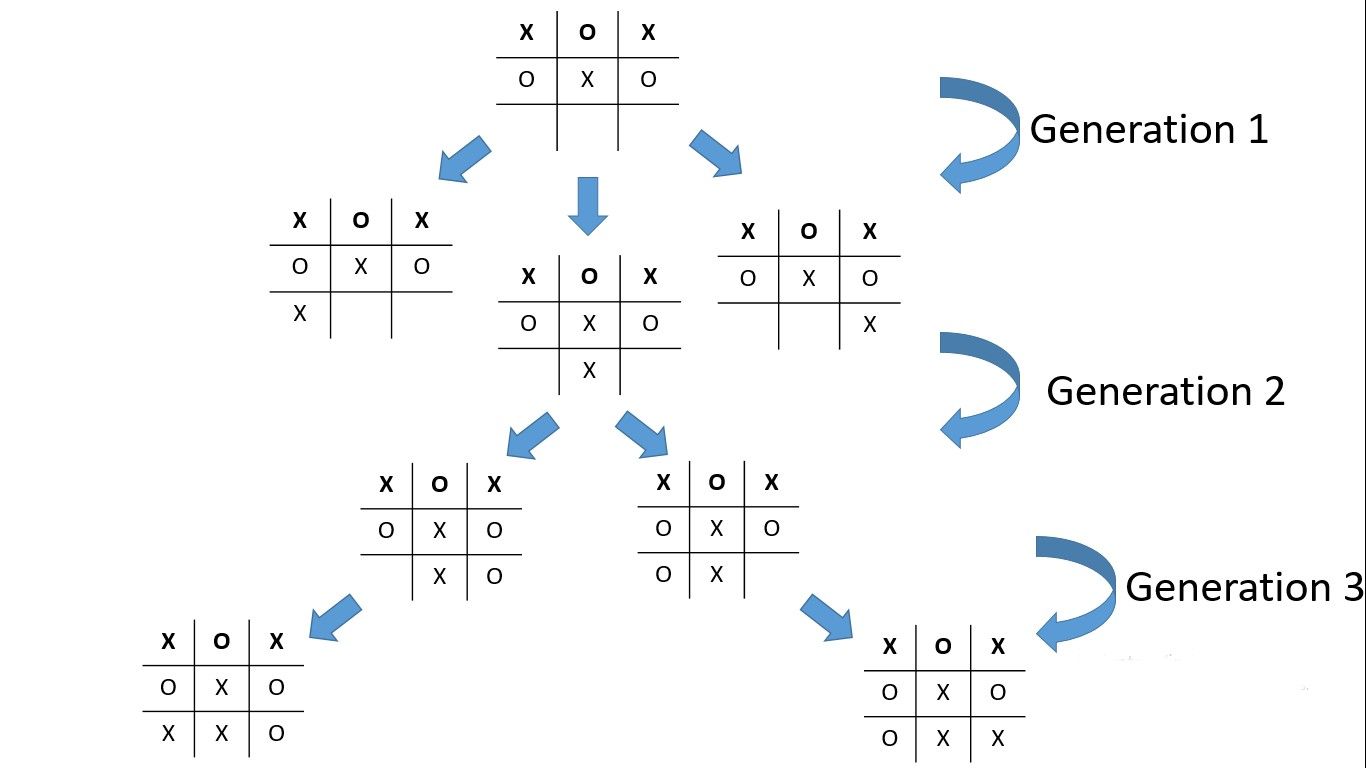
我们可以使用递归来实现这一点。我将在最后展示代码,但现在,让我们专注于理解如何处理游戏组合以获得最佳棋步。我们将考虑这些情况:
- 棋盘上有一个 X 的获胜位置,等于 1 分
- 棋盘上有一个 O 的获胜位置,等于 -1 分
- 棋盘上有一个平局的位置,等于 0 分
如果我们要为 X 找到最佳棋步,我们应该找到分数最多的棋盘。但是如果一个棋盘还没有完成呢?那么我们应该根据它的子棋盘来选择棋盘——但我们该选择哪一个呢?
我需要你专注于这部分,因为这是最重要的部分。当我介绍这个算法时,我说它能找到所有的游戏组合,假设双方都在采取最优的棋步。
在第一代子棋盘之后,就会轮到 O 了。假设 O 是在采取最优棋步,我们应该选择一个 O 做得最好的棋盘,也就是分数最少的棋盘之一(因为当 O 赢的时候,该棋盘会返回 -1)。
为什么我们要这样选择呢?想象一下,如果我们在轮到 O 的时候选择最大值,那么我们就会让 X 获胜。这使得该算法毫无用处,因为我们需要假设 O 以最佳棋步下棋。
对于第三代,玩家又是 X,我们将再一次选择点数最多的棋盘。
这种交替选择最大值和最小值的方法就是这个算法被称为极小化极大值算法的原因。请看这个可视化图,以进一步了解:
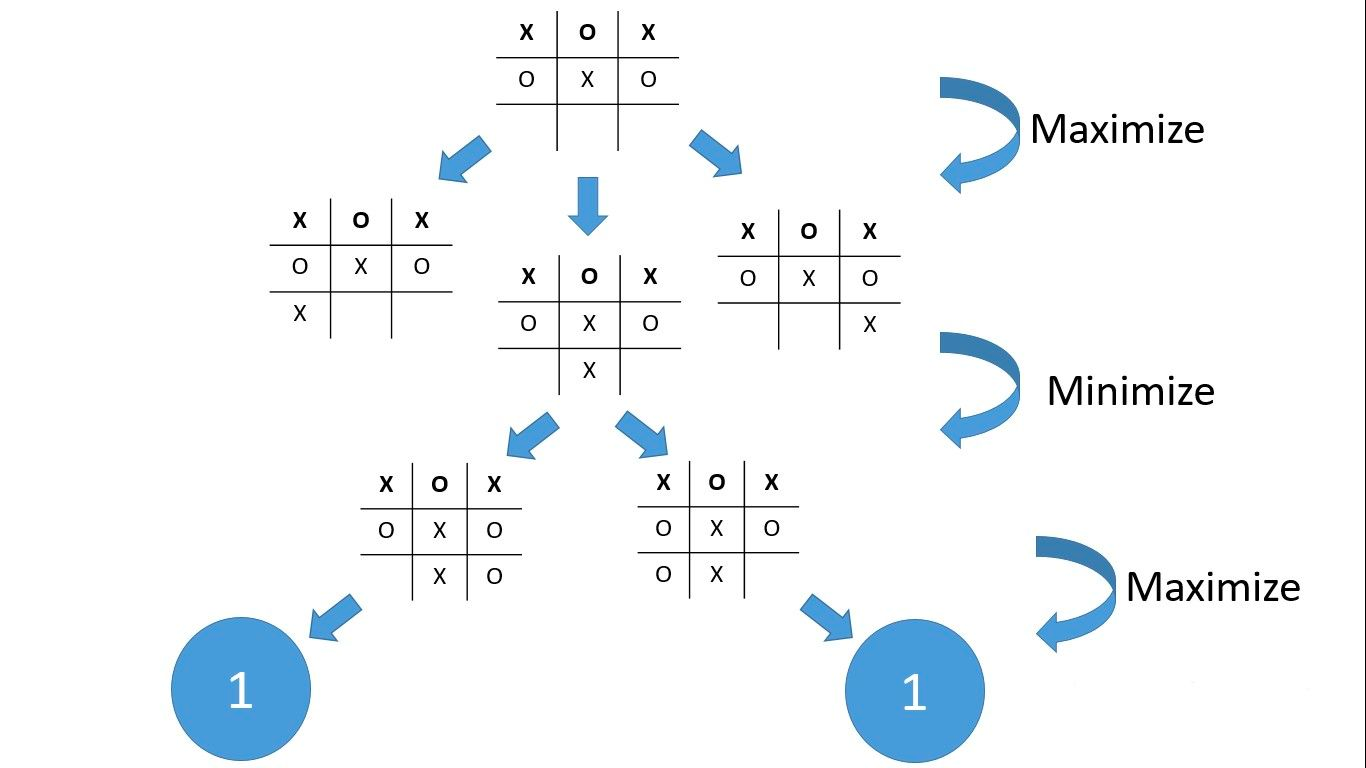
这与上面的例子相同。底部的 2 个棋盘对 X 来说是赢的,所以每个棋盘都会返回 1。这里,轮到 X 了,所以我们会选择最佳值——恰好这两个棋盘的值都是 1。
正如我之前所说,如果一个棋盘不满足获胜或平局条件,我们将查看其子棋盘。这就是为什么数值为 1 的棋盘的父棋盘会有 1 的数值。
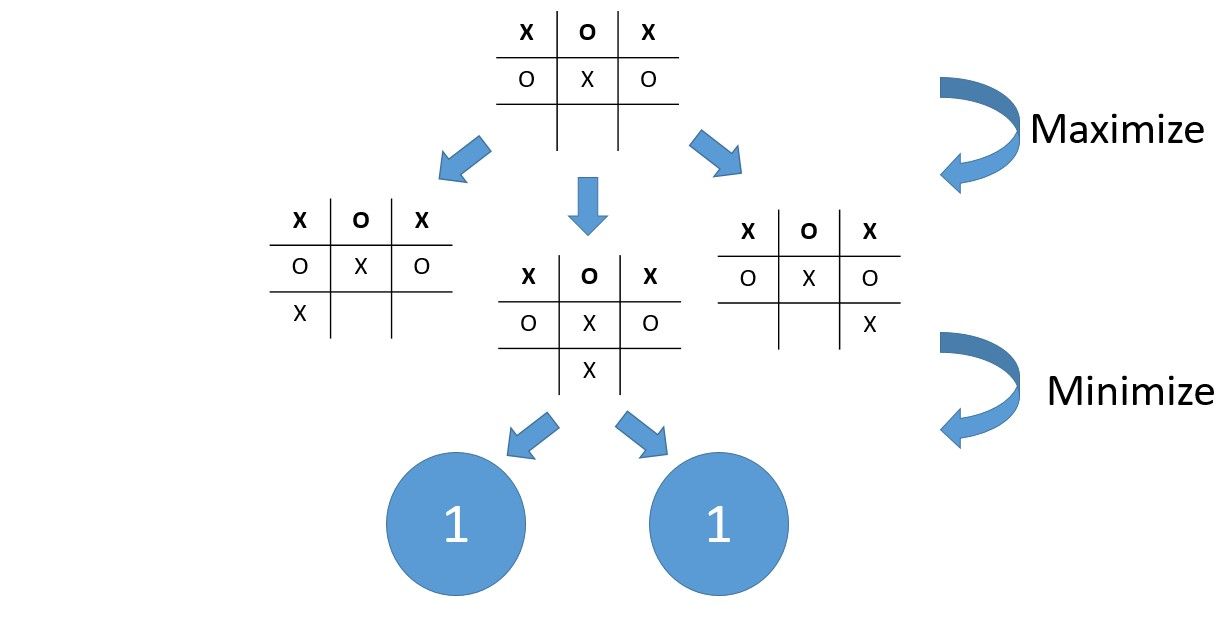
这里轮到 O,所以我们将选择可能的最低值,恰好是 1。我选择这个特定的例子是为了让事情变得简单,但这在所有棋盘上都适用。

最后又轮到了 X,我们将最大化所选棋盘的值。这就是为什么我们可以选择左边的子棋盘或右边的子棋盘或中间的子棋盘——这并不重要,因为它们的值是一样的。
最后,X 的最佳棋步是在第 7、8 或 9 位,以最大限度地提高其获胜的机会。如果你仍然不相信,可以取任何棋盘组合并画出组合树,你会得到一个满意的结果——我强烈建议在纸上画出来。
Minimax 算法的局限性
正如你所看到的,该算法是递归的,执行次数可能会变得很大。
例如,对于井字游戏,执行次数大约为 “9!”(9 的阶乘)。原因是第一步棋有 9 种可能性,然后每一步棋有 8 种可能性,以此类推。
这对井字棋来说不是问题,但考虑一下国际象棋游戏。如果我们要写出组合的数量,整个宇宙都不够用了。所以,最小值经常被用作引擎的一部分,但它不足以满足我们的需要。
如何提高算法的时间复杂度
你可能已经注意到,使用这种方法可能会导致一些重复的棋盘,我们需要多次计算它们的值。那么,为什么不在计算时存储每个棋盘的值呢?
所以现在,对于每一次迭代,我们将检查一个位置是否已经发生过。如果是的话,我们将使用它的存储值。否则,我们可以计算出位置的值,然后将其存储。
对于存储值,我们将使用一个字典,允许在 O(1) 中进行搜索。使用这种方法,我们可以降低时间复杂度——但在某些情况下,它仍然是无效的。
我曾经用这种算法做了一个四子棋游戏,它的运行时间很糟糕。因此,我没有寻找所有的组合,而是在一定的深度上停下来,这生成了一个可以提前看到 n 步的 AI。
如果你有兴趣,可以看看这个 GitHub 仓库里的四子游戏代码。我是很久以前写的,但仍然值得一看。
井字游戏 AI 代码
现在我们先来实现一些辅助函数。我们将首先检查棋盘数组中是否有 3 个水平、垂直或对角线的非空字符串值。
// 棋盘数组
let xo=['','','',
'','','',
'','','']
// 编写这个函数时,我们需要确保相等的值不是空字符串
// 在这之前,我将写一个辅助函数来确保 3 个索引没有空字符串
function helper(index1,index2,index3){
return xo[index1] !='' && xo[index2] !='' && xo[index3]!=''
}
function checkwin(){
return (xo[0]==xo[1] && xo[1] ==xo[2] && helper(0,1,2)) ||
(xo[3]==xo[4] && xo[4] ==xo[5] && helper(3,4,5)) ||
(xo[6]==xo[7] && xo[7] ==xo[8] && helper(6,7,8)) ||
(xo[0]==xo[3] && xo[3] ==xo[6] && helper(0,3,6)) ||
(xo[1]==xo[4] && xo[4] ==xo[7] && helper(1,4,7)) ||
(xo[2]==xo[5] && xo[5] ==xo[8] && helper(2,5,8)) ||
(xo[0]==xo[4] && xo[4] ==xo[8] && helper(0,4,8)) ||
(xo[2]==xo[4] && xo[4] ==xo[6] && helper(2,4,6))
}
// 最后是一个检查是否有平局的函数,它将检查所有的棋盘值是否为空字符串。这个函数只有在首先检查了没有获胜条件之后才会起作用。
function boardfull(){
return xo.every((elem)=>{
return elem !=''
})
}现在我们有了检查是否存在获胜状态的函数,我们最终可以像这样写出 Minimax(我在代码中添加了注释以帮助解释)。
// 正如我之前所说的,算法将通过 board 和 ismax 参数来检查我们是否要最大化或最小化某一个回合
function minimax(board,depth,ismax){
// 这是一个递归函数,所以我们应该首先设置基本情况,这将是获得平局、胜利或达到深度。
// 正如你在可视化中所看到的,当出现平局或获胜条件时,不会再产生子棋盘。因此,如果在轮到 X 的时候发生了获胜的条件。赢的是 X,这就是我返回 1 的原因,同样的逻辑也适用于 Y 赢时,我在最小化时返回 -1。
if (checkwin()) return ismax ? 1 : -1
if (boardfull()) return 0
if(ismax){
// 当我们进行最大化时,我们将设置一个计数器为 -Infinity,只要我们遇到一个高于计数器的棋盘值,我们就将其视为最佳棋步。
let best=-Infinity
board.forEach((elem,index)=>{
// 现在,为了检查所有产生的位置,我们将在棋盘上进行迭代,只要有一个可用的,我们就将其设置为 X,并在这个位置上运行 minimax。
if(elem ==''){
board[index]='X'
let localscores=minimax(test,depth+1,false)
// 我在这里把棋盘重新设置到相同的位置
board[index]=''
best=max(best,localscores)
}})
return best
}
// 这里的 else 意味着我们正在最小化
else{
// 在这里,我们将设置我们的计数器为 + Infinity,因为我们想找到可能的最低值
let best=Infinity
board.forEach((elem,index)=>{
if(elem ==''){
board[index]=humanicon
let localscores=minimax(test,depth+1,true)
board[index]=''
best=min(best,localscores)
}})
return best
}
}我们完成了!
总结
在这篇文章中,我们了解了 Minimax 算法、它的机制、它的局限性,以及如何改进它。现在你可以去定制 Minimax 算法,使其在各种游戏中运行,创造一些很酷的游戏机器人。
最后,我希望你从这篇文章中学到一些新东西。
如果你觉得这篇文章很有用,并想获得更多精彩的内容,请在 LinkedIn 上关注我。这将会有很大的帮助。


