Two-player turn-based games are games where two players play against each other, turn after turn, until one of them wins. Examples of these types of games are Tic-Tac-Toe, Backgammon, Mancala, Chess, and Connect 4.
In this tutorial we will learn about the Minimax algorithm. It is a backtracking algorithm that is used in decision making and game theory. It finds the optimal move for a player, assuming their opponent also plays optimally. It is widely used in two-player turn-based games.
You will learn how to create your own AI that plays any of the games mentioned above or any other similar games. Also, to make this as comprehensible as possible, I will be applying the algorithm to a Tic-Tac-Toe game.
We will not cover the whole process of creating the game, but only the part related to AI since this is our topic. If you're interested in the game-creating process, you can check out this Tic-Tac-Toe game that uses AI and its source code on GitHub. It's a project that I built long ago but it's still one of my favorites.
Table of contents
- How the minimax algorithm works
- Limitations of the minimax algorithm
- How to improve the time complexity of the algorithm
- Tic-Tac-Toe AI Code
- Conclusion
How the Minimax Algorithm Works
The minimax algorithm's methodology is quite simple. First, it checks all the possible combinations from a given position. Then it chooses the best possible move that maximizes the chances of winning, assuming that both players play perfectly.
To illustrate this, let’s consider a Tic-Tac-Toe game to make this more convincing. As you might know, in this game there are 2 players and 9 available slots. So we can represent a game by using an array of length 9.
Now let's take this board as an example: as you can see, a game board is an array of length 9 whose values can be either X, O, or an empty string. An empty string means this position is still available.

Now it's X's turn. The minimax algorithm will try all the game combinations from this position. Then it'll try all the game combinations from the resulting child positions until reaching a position where the game ends by either X winning, O winning, or a draw (which occurs when the board is full and no one is winning).
This picture illustrates how this works:
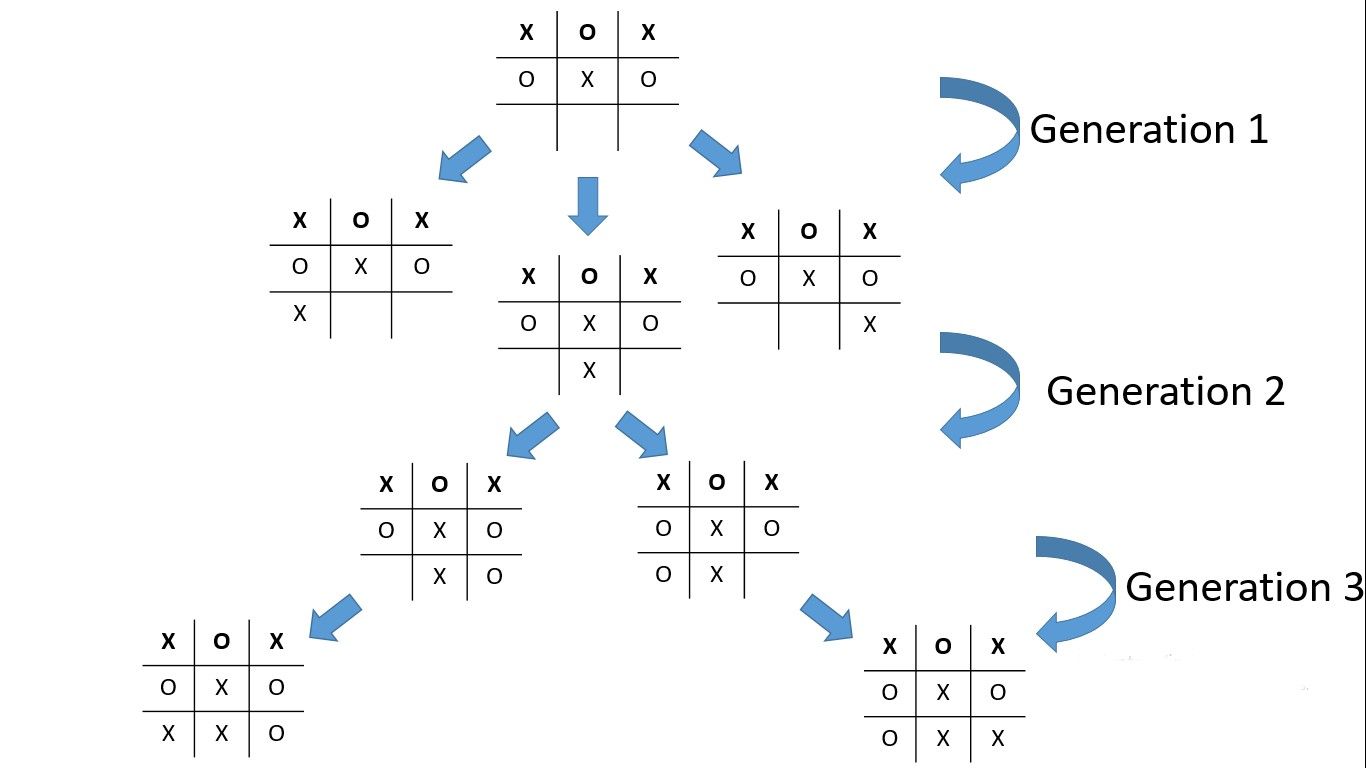
We can achieve this using recursion. I will show the code at the end, but for now, let's focus on understanding how we can process the game combinations to get the optimal move. We will consider these cases:
- The board which has a winning position for X is valued by 1 point
- The board which has a winning position for O is valued by -1 point
- The board where the position is a draw has 0 points
If we're finding the optimal move for X, we should find the board with the most points. But what if a board isn't finished yet? Then we should choose a board depending on its child boards – but which do we choose?
I need you to focus on this part, as it's the most important part. When I introduced the algorithm I said that it finds all the game combinations assuming both players are playing optimally.
After the first generation of child boards, it will be O's turn. With the assumption that O is playing optimally, we should choose a board where O is doing his best that is one of the boards with the fewest points (since when O wins, the board returns -1).
Why are we choosing like this? Imagine if we pick the maximum value when it's O's turn, then we're letting X win. This makes the algorithm useless, since we need to assume O plays optimally.
For the 3rd generation, the player is X again and we will choose the board with the most points once more.
This alternating method of choosing the maximum and the minimum values is the reason why this algorithm is called the Minimax algorithm. Check out this visualization for further clarification:

This is the same example given above. The 2 boards at the bottom are winning for X, so each will return a value of 1. Here, it’s X’s turn so we will pick the optimal value - it happens that both boards have a value of 1 here.
As I said earlier, if a board doesn't satisfy winning or drawing conditions, we will look at its child boards. That's why the parents of the boards with value 1 will have a value of 1.
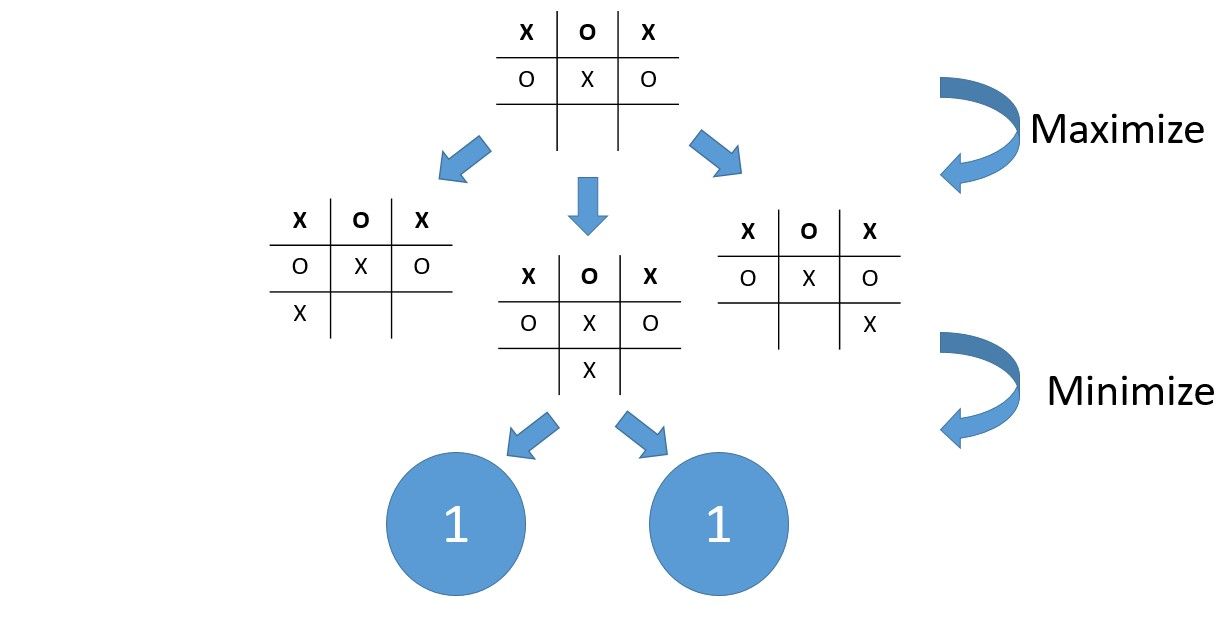
Here it's O's turn so we will pick the lowest possible value which happens to be 1. I've chosen this specific example to make things simple, but this works on all boards.

Finally it's X's turn again and we will maximize the value of the chosen board. That’s why we can choose the child board on the left or the one on the right or the one in the middle – it doesn’t matter since their values are the same.
In the end, the optimal move for X to maximize its winning chances is in positions 7, 8 or 9. If you're still not convinced, take any board combination and draw the combination tree and you'll get a satisfying result - I strongly recommend drawing this on paper.
Limitations of the Minimax Algorithm
As you've seen, the algorithm is recursive and the number of executions may become huge.
For example, for a Tic-Tac-Toe game the number of executions is approximately “9!”(9 factorial). The reason why is for the first move there are 9 possibilities and then for each subsequent move there are 8 and so on.
That's not a problem for tic-tac-toe, but consider a chess game. If we were to write the number of combinations, the entire universe would not be enough. So the minimax is often used as part of an engine but it’s not enough to fulfill our needs.
How to Improve the Time Complexity of the Algorithm
You may have noticed that using this approach may result in some repetitive boards and that we need to compute their value multiple times. So why not store the value of every board when calculated?
So now, for every iteration, we will check if a position has already occurred. If so, we will use its stored value. Else, we can compute the value of the position and then store it.
For storing values, we will use a dictionary which allows searching in O(1). Using this approach we can reduce the time complexity – but still, it wouldn't be efficient in some cases.
I’ve built a Connect 4 game with this algorithm and it was horrible in terms of runtime. So, instead of looking for all the combinations, I stopped at a certain depth which led to an AI that can see n moves ahead.
If you're interested, check out this GitHub repository for the Connect 4 game code. I wrote it a long time ago but it's cool to see.
Tic-Tac-Toe AI Code
Now let's implement some helper functions first. We will first check if there are 3 horizontal, vertical, or diagonal non-empty string values in the board array.
// Board array
let xo=['','','',
'','','',
'','','']
// Writing this function we need to make sure the equal values are not empty strings
// Before this I will write a helper function to make sure 3 indexes have no empty strings
function helper(index1,index2,index3){
return xo[index1] !='' && xo[index2] !='' && xo[index3]!=''
}
function checkwin(){
return (xo[0]==xo[1] && xo[1] ==xo[2] && helper(0,1,2)) ||
(xo[3]==xo[4] && xo[4] ==xo[5] && helper(3,4,5)) ||
(xo[6]==xo[7] && xo[7] ==xo[8] && helper(6,7,8)) ||
(xo[0]==xo[3] && xo[3] ==xo[6] && helper(0,3,6)) ||
(xo[1]==xo[4] && xo[4] ==xo[7] && helper(1,4,7)) ||
(xo[2]==xo[5] && xo[5] ==xo[8] && helper(2,5,8)) ||
(xo[0]==xo[4] && xo[4] ==xo[8] && helper(0,4,8)) ||
(xo[2]==xo[4] && xo[4] ==xo[6] && helper(2,4,6))
}
//And finally a function to check if there is a draw which will check if all board values are not empty strings. This only works after checking that there is no winning conditions first
function boardfull(){
return xo.every((elem)=>{
return elem !=''
})
}Now we have the function to check if a winning state is there and we can finally write the Minimax like this (I've added comments in the code to help explain it):
// As I said erlier, the algorithm will take the board, the ismax parameter to check if we want to maximize or minimize for a certain turn
function minimax(board,depth,ismax){
// This is a recursive function, so we should set the bases cases first which will be getting a draw a win or reaching the depth
// As you've seen in the visualizations, when there is a draw or winning conditions no more child boards are generated. So if a winning condition occured when it's X's turn. It got to be X who won that's why I returned 1, and the same logic applies for when Y won and I returned -1 when we were minimizing.
if (checkwin()) return ismax ? 1 : -1
if (boardfull()) return 0
if(ismax){
// When we're maximizing we will set a counter to -Infinity and whenever we encounter a board value higher than the counter, we will consider it as the best move
let best=-Infinity
board.forEach((elem,index)=>{
//Now to check all resulting positions we will iterate over the board and whenever there is an avaible slot we will set it to X and run minimax on this position. Look how I incrimented the depth
if(elem ==''){
board[index]='X'
let localscores=minimax(test,depth+1,false)
// Here I am reetting the board to the same position
board[index]=''
best=max(best,localscores)
}})
return best
}
// This else here means we're minimizing
else{
// Here we will set our counter to + Infinity because we want to find the lowest possible value
let best=Infinity
board.forEach((elem,index)=>{
if(elem ==''){
board[index]=humanicon
let localscores=minimax(test,depth+1,true)
board[index]=''
best=min(best,localscores)
}})
return best
}
}And now we're done!
Conclusion
In this article, we’ve learned about the minimax algorithm, its mechanism, limitations, and how to improve it. Now you can go and customize this to work on various games to create some cool game bots.
In the end, I hope you learned something new from this article.
If you found this useful and want to get more awesome content, follow me on LinkedIn. It will help a lot.

