Guía de cálculo científico en Python. Matemáticas en SciPy y NumPy explicadas con ejemplos

SciPy y NumPy son bibliotecas de Python que se utilizan comúnmente en cálculo científico y en ciencia de datos.

NumPy proporciona una infraestructura para trabajar con arreglos numéricos y matrices, mientras que SciPy proporciona una amplia gama de algoritmos numéricos, cálculos matemáticos avanzados y herramientas para aplicaciones científicas.

Una de las principales razones por las que estas bibliotecas son tan populares en el ámbito científico es porque son muy eficientes en el manejo de grandes conjuntos de datos numéricos y matrices.

Además, SciPy y NumPy tienen una gran cantidad de funciones integradas para realizar operaciones numéricas complejas, como la transformada de Fourier, la optimización numérica, el álgebra lineal, la estadística y el procesamiento de señales.

Estas funciones son esenciales en muchas aplicaciones científicas, desde el procesamiento de imágenes hasta el análisis de datos biomédicos. Sin embargo, esto no excluye que podamos emplearlas para resolver problemas más burdos.

Otro aspecto importante es que ambas bibliotecas son de código abierto y tienen una gran comunidad de desarrolladores, lo que permite que los usuarios obtengan soporte y contribuyan a la mejora de las bibliotecas.

Motivo y enfoque de este artículo

Este artículo busca proporcionar una visión general aunque no por ello ligera, sobre algunas de las aplicaciones matemáticas y estadísticas que pueden tener NumPy y SciPy.

Si bien, ya existe información acerca de estas librerías, -especialmente sobre NumPy-. El enfoque de este contenido será dar un pantallazo amplio pero detallado a las principales aplicaciones científicas de estas librerías. No tanto así a un "procedimiento" en específico. Si por otra parte requieres de un tutorial más concreto te recomiendo esta guía y este curso de arreglos en NumPy.

Habiendo aclarado esto, en este artículo se presentan varias aplicaciones científicas y prácticas de SciPy y NumPy. Ya sea que te interesen los aspectos más teóricos de la ciencia de datos, tengas una profesión científica o de ingeniería, seas estudiante de carreras cuantitativas, o simplemente busques crecer en el desarrollo de aplicaciones especializadas; este tutorial podría serte útil.

Tres notas o más bien "disclaimers" antes de empezar:

1. Este artículo se centra en el desarrollo de varios problemas matemáticos y científicos y pese a que traté de organizarlos en un orden más o menos coherente algún ejercicio puede resultar chocante, o difícil de entender a nivel teórico. Mi consejo es el siguiente: Toma lo que te sirva, no te preocupes por tratar de entenderlo todo, aunque, desde luego, tampoco hay quejas si lo entiendes el 100% :D.
2. Debido a que son ejercicios separados verás repetidamente "import matplotlib.pyplot as plt" o import numpy as np. Sé que es redundante, pero la idea que es todos los ejercicios estén listos "para tomar" y tratar de replicarlos sin preocuparte por el orden.
3. Siento no poder incluir ejemplos de otros campos -eg. como la física o la epidemiología-, pero carezco de la formación para ello.

Bien, ahora sin más preámbulos pasemos a los ejercicios.

Estadística y probabilidad con SciPy y NumPy

Método de Montecarlo

El código presentado es una implementación de un método de simulación para estimar el valor de π (pi). La idea detrás del método es simular el lanzamiento de dardos aleatorios sobre un cuadrado con un círculo inscrito. Al lanzar dardos aleatorios, podemos contar cuántos de ellos caen dentro del círculo y cuántos fuera.

Con esta información, podemos hacer una estimación del área del círculo y, por lo tanto, del valor de π.

El código utiliza la biblioteca NumPy para generar coordenadas aleatorias para los dardos y para realizar operaciones matemáticas. La biblioteca SciPy se utiliza para calcular la función de densidad de probabilidad acumulada, que se utiliza para determinar cuántos dardos caen dentro del círculo.

#Cálculo del número PI de forma aleatoria
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats

# Número de dardos a lanzar
N = 1000000

# Generar coordenadas aleatorias
x = np.random.uniform(low=-1, high=1, size=N)
y = np.random.uniform(low=-1, high=1, size=N)

# Calcular la distancia al centro
dist = np.sqrt(x**2 + y**2)

# Calcular el número de dardos que caen dentro del círculo
num_dentro = np.sum(dist < 1)

# Estimar pi
pi_estimado = 4 * num_dentro / N

# Comparar con el valor real de pi
pi_real = np.pi
error_relativo = np.abs(pi_estimado - pi_real) / pi_real

# Mostrar resultados
print(f"Valor estimado de pi: {pi_estimado}")
print(f"Valor real de pi: {pi_real}")
print(f"Error relativo: {error_relativo}")

#Visualización del círculo de pi
fig, ax = plt.subplots(figsize=(7, 7))
ax.set_aspect('equal')
circulo = plt.Circle((0, 0), 1, color='grey', alpha=0.2)
ax.add_artist(circulo)
ax.scatter(x[dist < 1], y[dist < 1], s=0.5, color='white')
ax.scatter(x[dist >= 1], y[dist >= 1], s=0.5, color='turquoise')

# Mostrar resultados gráficamente
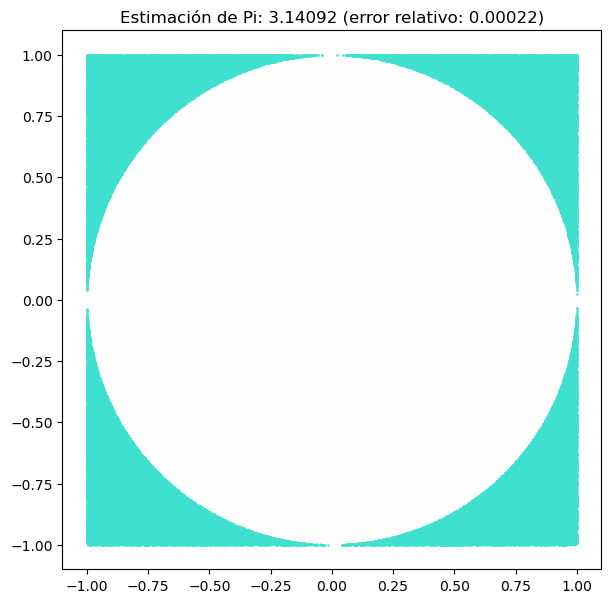
ax.set_title(f"Estimación de Pi: {pi_estimado:.5f} (error relativo: {error_relativo:.5f})")
plt.show()

#Resultados
Valor estimado de pi: 3.143684
Valor real de pi: 3.141592653589793
Error relativo: 0.0006656962378038079
#Nuestro número estimado se aproxima mucho al número pi!

Primero, el número de dardos que se lanzará se define como N=1000000. A continuación, se generan coordenadas aleatorias para los dardos utilizando la función np.random.uniform(). Se genera un conjunto de coordenadas para la coordenada x y otro para la coordenada y, ambos en el rango de [-1, 1].

Luego, se calcula la distancia euclidiana desde el origen de cada punto generado. Si la distancia es menor que 1, significa que el punto cae dentro del círculo. Se cuentan cuántos puntos caen dentro del círculo mediante np.sum() y np.where().

Una vez se tiene el número de puntos que caen dentro del círculo, se estima el valor de π mediante la fórmula π = 4 * puntos dentro del círculo / total de puntos.

Por último, se comparan el valor estimado de π con el valor real y se muestra el error relativo en la estimación.

Este método de simulación es muy útil ya que puede ser utilizado para estimar π en cualquier dimensión. Además, este método se puede utilizar para simular cualquier otro problema donde se desee obtener una estimación numérica de una cantidad desconocida.

Ajustando una curva de datos

Estos son dos ejemplos de cómo ajustar una curva de datos con una función, utilizando la biblioteca NumPy, Matplotlib y SciPy de Python.

En general, el ajuste de curvas es un proceso importante en el análisis de datos que se utiliza para encontrar relaciones funcionales entre las variables. Los modelos que se ajustan pueden variar desde simples funciones polinómicas hasta modelos más complejos con múltiples parámetros.

El ajuste de curvas es una herramienta útil para la predicción y la interpretación de los datos, especialmente en áreas como la estadística, la física, la ingeniería y la ciencia de datos.

#Ajustando una curva de datos
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# Datos
x = np.array([1, 2, 3, 4, 5])
y = np.array([1.1, 3.5, 7.2, 13.1, 21.3])

# Función a ajustar
def func(x, a, b, c):
    return a * x**2 + b * x + c

# Ajuste
popt, pcov = curve_fit(func, x, y)

# Coeficientes
a, b, c = popt

# Gráfica
plt.plot(x, y, 'ro', label='Datos')
plt.plot(x, func(x, a, b, c), label='Ajuste')
plt.legend()
plt.show()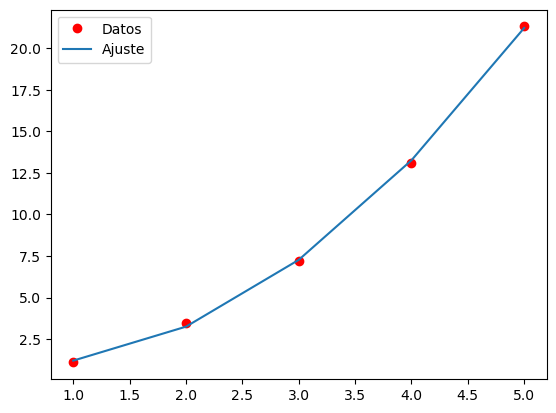

#Ejemplo 2
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

# Función a la que se quiere ajustar la curva
def func(x, a, b, c):
    return a*np.exp(-b*x) + c

# Datos a los que se quiere ajustar la curva
xdata = np.linspace(0, 4, 50)
ydata = func(xdata, 2.5, 1.3, 0.5) + 0.2*np.random.normal(size=len(xdata))

# Ajuste de la curva
popt, pcov = curve_fit(func, xdata, ydata)

# Graficar los datos y la curva ajustada
plt.plot(xdata, ydata, 'o', label='Datos')
plt.plot(xdata, func(xdata, *popt), '-', label='Curva ajustada')
plt.legend()
plt.show()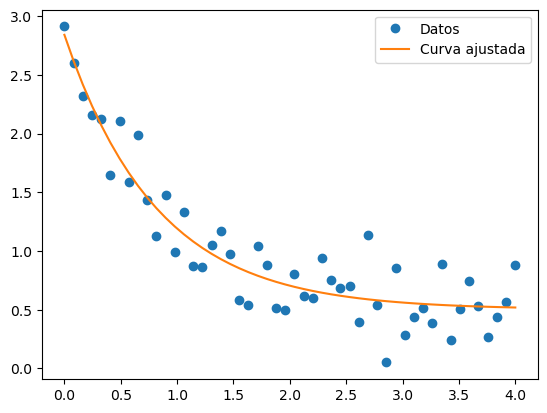

Aquí hemos visto como ajustar una curva de datos con una función, utilizando la biblioteca NumPy, Matplotlib y SciPy de Python.

Primero, se definen dos matrices NumPy de 1D, x e y, que contienen los datos de los puntos a ajustar. Luego se define una función "func" que se utilizará para realizar el ajuste de la curva. Esta función toma tres argumentos, a, b y c, que son los coeficientes de la función cuadrática ax^2 + bx + c.

El ajuste de la curva se realiza utilizando la función curve_fit de SciPy. Esta función devuelve dos valores, popt y pcov. El primero es una matriz NumPy de 1D que contiene los valores óptimos para a, b y c, y el segundo es una matriz NumPy de 2D que contiene la covarianza de los parámetros.

A continuación, se asignan los valores óptimos de los coeficientes a, b y c a variables separadas a partir de popt. A continuación, se grafican los puntos de datos originales junto con la curva ajustada utilizando la función plot de Matplotlib.

Medidas de dispersión

Las medidas de dispersión son estadísticas que indican cuánto se alejan los datos de un conjunto de valores respecto a su valor central o promedio. Estas medidas se utilizan para analizar la variabilidad o heterogeneidad de los datos.

#Medidas de dispersión en Numpy y Scipy
import numpy as np
from scipy import stats

import numpy as np

# Datos
datos = np.array([4, 49, 19, 4, 14, 20, 17, 50, 4, 20])

# Media
media = np.mean(datos)
print("Media:", media)

# Mediana
mediana = np.median(datos)
print("Mediana:", mediana)

# Desviación estándar
desviacion_estandar = np.std(datos)
print("Desviación estándar:", desviacion_estandar)

# Moda
moda = stats.mode(datos)
print("Moda:", moda.mode[0])

#Resultado
Media: 20.1
Mediana: 18.0
Desviación estándar: 15.984054554461457
Moda: 4

Aquí se define una lista de datos llamada "data".La media, mediana y desviación estándar de los datos se calculan utilizando las funciones "mean", "median" y "std" de NumPy. Nótese que para el caso de la moda recurrimos a SciPy.

La media es la suma de todos los valores dividida por el número de valores, la mediana es el valor que se encuentra en el centro de un conjunto de datos ordenados, y la desviación estándar mide la cantidad de variabilidad o dispersión en los datos. La moda por su parte, es el valor que más se repite en la serie.

Ajuste de regresión lineal

Anteriormente vimos el ajuste de curva, esta vez veremos un ajuste parecido pero limitado a la regresión lineal, y por tanto, de una mayor aplicación estarística.

El ajuste de curva permite modelar una amplia variedad de formas de curva, mientras que el ajuste de regresión lineal se limita a modelos lineales. Pero esa no es la única diferencia. El primero es más una mera optimización, mientras que con el ajuste de regresión lineal, nos jugamos la integridad de todo el modelo estadístico, de allí que en esta ocasión trajemos con 'stats'.

#Ajuste de modelo de regresión lineal
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Datos de ejemplo
x = np.array([10, 20, 30, 40, 50, 60])
y = np.array([2.5, 5.1, 7.3, 9.1, 11.2, 13.5])

# Ajuste de modelo de regresión lineal
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)

# Imprimir resultados
print(f"Coeficiente de pendiente: {slope}")
print(f"Coeficiente de intersección: {intercept}")
print(f"Coeficiente de correlación: {r_value}")
print(f"Valor p: {p_value}")
print(f"Error estándar: {std_err}")

#Graficando los datos originales y la línea de regresión
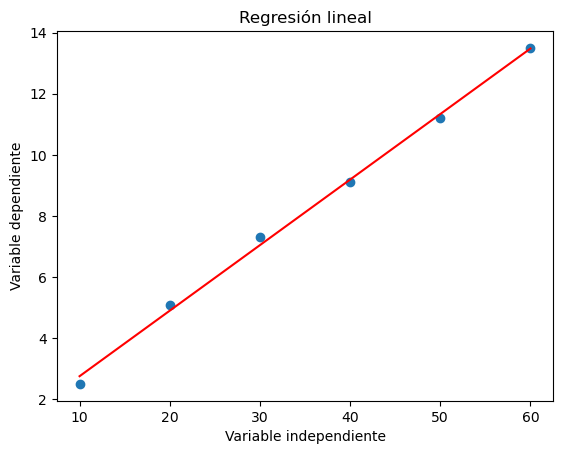
plt.scatter(x, y)
plt.plot(x, slope*x + intercept, color='red')
plt.title('Regresión lineal')
plt.xlabel('Variable independiente')
plt.ylabel('Variable dependiente')
plt.show()

#Resutado
Coeficiente de pendiente: 0.21457142857142858
Coeficiente de intersección: 0.6066666666666665
Coeficiente de correlación: 0.998781193835107
Valor p: 2.227327440120712e-06
Error estándar: 0.0053017773941776

Este código realiza un ajuste de modelo de regresión lineal a un conjunto de datos utilizando la biblioteca SciPy.

Primero, se definen los datos de ejemplo x e y como matrices NumPy. Luego, se utiliza la función stats.linregress(x, y) de SciPy para realizar el ajuste de regresión lineal.

La función stats.linregress() devuelve cinco valores: la pendiente (slope), la intersección (intercept), el coeficiente de correlación (r_value), el valor p (p_value) y el error estándar (std_err).

Matemáticas financieras

Pasemos ahora a ver un par de aplicaciones de estas bibliotecas a las matemáticas financieras.

#Matemáticas financieras con Numpy
#Comenzamos instalando el paquete numpy-financial
pip install numpy-financial

#Calculando el VAN
import numpy_financial as npf

# Datos de entrada
tasa_descuento = 0.1
flujos_efectivo = [-100, 60, 60, 60, 60]
inversion_inicial = 100

# Cálculo del valor presente neto
vpn = npf.npv(tasa_descuento, flujos_efectivo) + inversion_inicial

print("El valor presente neto es:", round(vpn, 2))

#Resultado
El valor presente neto es: 190.19

El código anterior muestra cómo calcular el valor presente neto de una serie de flujos de efectivo utilizando la biblioteca numpy_financial. Recuerda primero instalar la librería Numpy Financial.

Primero, se definen las variables de entrada del problema. La tasa de descuento se establece en 0.1, lo que significa que se asume que el costo de oportunidad del capital es del 10%. Los flujos de efectivo se dan como una lista de valores. En este caso, hay un flujo inicial de efectivo de -100, lo que significa que hay una inversión inicial de 100, seguido de cuatro flujos positivos de efectivo de 60.

Luego, se utiliza la función npf.npv() de la biblioteca numpy_financial para calcular el valor presente neto de los flujos de efectivo. Esta función toma como argumentos la tasa de descuento y una lista de flujos de efectivo. También se agrega la inversión inicial al resultado final.

Finalmente, el valor presente neto se imprime en la pantalla redondeado a dos decimales.

El valor presente neto es una herramienta útil en la toma de decisiones de inversión, ya que permite evaluar la rentabilidad de un proyecto de inversión. Si el valor presente neto es positivo, significa que el proyecto es rentable, mientras que un valor negativo indica que el proyecto no es rentable.

#Calculando la TIR
import numpy_financial as npf

flujos_efectivo = [-1000, 200, 250, 300, 350, 400, 450]
tir = npf.irr(flujos_efectivo)

print("La TIR es:", round(tir, 4))

#Resultado
La TIR es: 0.1979

A continuación hemos utilizado la librería numpy_financial para calcular la TIR (tasa interna de retorno) de un flujo de caja.

Primero, se define la lista de flujos de efectivo llamada flujos_efectivo. Esta lista contiene los flujos de efectivo del proyecto en diferentes periodos de tiempo. En este caso, el proyecto requiere una inversión inicial de -1000 unidades monetarias y se espera que genere flujos de efectivo de 200, 250, 300, 350, 400 y 450 unidades monetarias en cada uno de los siguientes 6 periodos.

Luego, se utiliza la función npf.irr de la librería numpy_financial para calcular la TIR. La TIR es la tasa de interés que hace que el valor presente neto (VPN) de los flujos de efectivo sea igual a cero. En otras palabras, es la tasa a la que el proyecto es rentable. La función npf.irr utiliza una técnica de interpolación para encontrar la tasa de descuento que hace que el VPN sea igual a cero.

Finalmente, se imprime el resultado redondeado a 4 decimales utilizando la función round(). En este caso, la TIR calculada es de aproximadamente 18.97%, lo que significa que el proyecto es rentable y ofrece un rendimiento superior al 18.97% de interés anual.

Álgebra lineal con NumPy y SciPy

Tanto SciPy como NumPy proporcionan un conjunto de módulos específicos para el álgebra lineal. Estos incluyen herramientas para la solución de sistemas de ecuaciones lineales, la diagonalización de matrices, la descomposición de valores singulares y la descomposición de matrices de covarianza, entre muchas otras aplicaciones.

Producto de dos matrices

El producto de dos matrices es una operación matemática que se realiza entre dos matrices y produce una nueva matriz como resultado.

#Álgebra lineal con numpy
import numpy as np

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])

c = np.dot(a, b)

print(c)

#Resultado
[[19 22]
 [43 50]]

Traspuesta de una matriz

La traspuesta de una matriz es simplemente una matriz en la que las filas y columnas han sido intercambiadas. En otras palabras, la traspuesta de una matriz es una matriz en la que las filas de la matriz original se convierten en columnas y las columnas se convierten en filas.

import numpy as np

a = np.array([[1, 2], [3, 4]])

b = np.transpose(a)

print(b)

#Resultado 
[[1 3]
 [2 4]]

Inversa de una matriz

La inversa de una matriz es una matriz que, al multiplicarse por la matriz original, produce la matriz identidad.

#Inversa de una matriz
import numpy as np
from scipy.linalg import inv

a = np.array([[1, 2], [3, 4]])

b = inv(a)

print(b)

#Resultado
[[-2.   1. ]
 [ 1.5 -0.5]]

Determinante de una matriz

Si bien podemos explicar el determinante de una matriz de muchas formas. En este artículo nos conformaremos con decir que el determinante de una matriz nos dice si una matriz posee inversa o no.

#Determinante de una matriz
import numpy as np
from scipy.linalg import det

a = np.array([[1, 2], [3, 4]])

b = det(a)

print(b)

#Resultado
-2.0

Eigenvalores

Solo como ejemplo, que sepas que el paquete de algebra lineal de SciPy no se limita a operaciones básicas con matrices, sino que también permite temas más avanzados .

#Eigenvalores
import numpy as np
from scipy.linalg import eig

a = np.array([[1, 2], [3, 4]])

b, c = eig(a)

print(b)
print(c)

#Resultado
[-0.37228132+0.j  5.37228132+0.j]
[[-0.82456484 -0.41597356]
 [ 0.56576746 -0.90937671]]

Esta función calcula los valores y vectores propios (también llamados eigenvalores y eigenvectores) de la matriz a.

La función eig devuelve dos matrices, b y c. La matriz b contiene los valores propios de a y la matriz c contiene los vectores propios de a, donde cada columna de c corresponde a un vector propio.

Sistemas de ecuaciones lineales

Esta función resuelve el sistema de ecuaciones lineales a x = b, donde a es la matriz definida anteriormente y b es el vector definido anteriormente, y devuelve el valor de x que satisface la ecuación. El resultado se almacena en la variable c.

import numpy as np
from scipy.linalg import solve

a = np.array([[1, 2], [3, 4]])
b = np.array([5, 6])

c = solve(a, b)

print(c)

#Resultado
[-4.   4.5]

Nota Final: Puedes encontrar la amalgama de funciones de algebra lineal de SciPy en su manual.

Cálculo diferencial e integral en NumPy y SciPy

El cálculo diferencial es el estudio del cambio y la tasa de cambio de funciones, mientras que el cálculo integral se ocupa de la acumulación de pequeños cambios para encontrar áreas, volúmenes y otros conceptos geométricos. Ambos temas son fundamentales en matemáticas y tienen una amplia gama de aplicaciones en ciencias físicas y sociales, ingeniería y otras áreas de la industria.

SciPy proporciona una serie de herramientas para trabajar con cálculo diferencial e integral, incluyendo la capacidad de integrar y diferenciar funciones de manera numérica. Algunas de las funciones clave incluyen scipy.integrate.quad para integrar funciones unidimensionales, scipy.integrate.nquad para integrar funciones de varias variables, y scipy.integrate.solve_ivp para resolver ecuaciones diferenciales ordinarias.

Además, SciPy tiene funciones para realizar la diferenciación numérica, lo que permite calcular la derivada de una función en un punto dado sin la necesidad de conocer la fórmula analítica de la función. Las funciones relevantes incluyen scipy.misc.derivative y scipy.interpolate.UnivariateSpline.

Veamos pues, solo unos cuantos ejemplos de este extenso campo de aplicación.

Derivadas

import numpy as np
from scipy.misc import derivative

# Definir la función para la que se calculará la derivada
def f(x):
    return x**2 + 2*x + 1

# Calcular la derivada de la función (evaluada) en x=2
derivada = derivative(f, 2)

# Imprimir la derivada
print(derivada)

#Resultado
6.0

Aquí no hicimos más que evaluar la función en 2. La derivada de la función es 2x+2, por lo que tenemos 2 (2) +2=6.  En este ejemplo lo vemos fácil pero la utilidad de SciPy radica en calcular derivadas mucho más complejas.

Derivadas Parciales

La derivada parcial de una función de varias variables es la derivada con respecto a cada una de esas variables manteniendo las otras como constantes.

import numpy as np
from scipy.misc import derivative

# Definir la función
def f(x,y):
    return x**2 + y**2

# Calcular la derivada parcial con respecto a x en el punto (1,2)
x0 = 1
y0 = 2
dx = 1e-6  # tamaño de paso para la derivada
df_dx = derivative(lambda x: f(x,y0), x0, dx=dx)

print(f"La derivada parcial de f(x,y) con respecto a x en el punto (1,2) es {df_dx:.2f}")

#Resultado
La derivada parcial de f(x,y) con respecto a x en el punto (1,2) es 2.00

La derivada parcial de f(x,y) = x^2 + y^2 con respecto a x es 2x, y evaluada en (1,2) nos da 2, ya que x en ese punto es igual a 1. Por lo tanto, la tasa de cambio instantánea de f en la dirección x en el punto (1,2) es 2.

Integrales

En este ejemplo vamos a empezar directamente con una integral definida. En el proceso veremos la función quad de SciPy para calcular la integral definida de f en el intervalo [0, 1].

Donde f es la función a integrar, a es el límite inferior de la integral y b es el límite superior de la integral.

La función quad utiliza un algoritmo de integración numérica para aproximar la integral definida de f. En este caso, la integral definida es:

from scipy.integrate import quad

# Definimos la función a integrar
def f(x):
    return x**2 + 2*x + 1

# Calculamos la integral definida entre 0 y 1
resultado, error = quad(f, 0, 1)

# Imprimimos el resultado
print(f"La integral definida es {resultado}")

#Resultado
La integral definida es 2.3333333333333335

Si lo hubieramos hecho "a mano" tendríamos que haber encontrado la primitiva de f: F(x) = (1/3)*x^3 + x^2 + x + C

Después nos habría tocado que evaluar la primitiva F(x) en los límites de integración [0,1] . La función quad de SciPy nos ahora este proceso y nos proporciona un valor aproximado de la integral sin conocer el valor de la constante de integración.

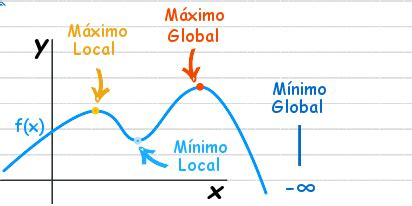
Mínimo Global

El mínimo global de una función es el valor más bajo que toma la función en todo su dominio. En otras palabras, es el punto más bajo en la gráfica de la función. Este valor representa el valor mínimo absoluto de la función, ya que no hay otro valor en el dominio de la función que produzca un resultado más bajo.

En términos matemáticos, un mínimo global es un valor "y" en la función "f(x)" que cumple con la condición de que "f(x) ≤ f(a)" para todos los valores de "x" en el dominio de la funció

from scipy.optimize import differential_evolution

# Definimos la función a minimizar
def f(x):
    return (x[0] - 1)**2 + (x[1] - 2.5)**2 + (x[2] - 5)**2

# Definimos los límites de búsqueda
limites = [(0, 5), (0, 5), (0, 10)]

# Buscamos el mínimo global
resultado = differential_evolution(f, limites)

# Imprimimos el resultado
print(f"El mínimo global es {resultado.x}")

#Resultado
El mínimo global es [1.  2.5 5. ]

Es importante recordar que solo hay un mínimo (y un máximo) global, aunque pueden haber diversos mínimos y máximos locales.

Series de Taylor

Las series de Taylor son una herramienta matemática utilizada para aproximar funciones mediante una serie infinita de términos polinómicos. La idea detrás de esta técnica es descomponer una función en términos de sus derivadas, lo que permite aproximar la función en un punto determinado.

import numpy as np
from scipy.misc import derivative
from scipy.special import factorial
from scipy import poly1d

# Función a la que queremos calcular la serie de Taylor
def f(x):
    return np.sin(x)

# Punto alrededor del cual queremos centrar la serie de Taylor
a = 0

# Orden de la serie de Taylor
n = 5

# Calculamos los coeficientes de la serie de Taylor utilizando la fórmula para la función seno
coeficientes = [(-1)**i/factorial(2*i+1) for i in range(n+1)]

# Creamos el polinomio a partir de los coeficientes
polinomio = poly1d(coeficientes)

# Evaluamos el polinomio en el punto x
x = 1
valor_aproximado = polinomio(x)

# Comparamos con el valor real de la función en el punto x
valor_real = f(x)
error_relativo = abs(valor_aproximado - valor_real)/valor_real

print(f"Valor aproximado: {valor_aproximado}")
print(f"Valor real: {valor_real}")
print(f"Error relativo: {error_relativo}")

#Resultado
Valor aproximado: 0.841470984648068
Valor real: 0.8414709848078965
Error relativo: 1.8993938788946215e-10

Este código calcula la serie de Taylor de la función seno en un punto específico y luego evalúa el polinomio de Taylor resultante en otro punto. A continuación, compara el valor aproximado obtenido a partir de la serie de Taylor con el valor real de la función en el punto evaluado, y calcula el error relativo.

Puedes encontrar una explicación más detallada y más técnica en el siguiente texto online.

Ecuaciones Diferenciales

from scipy.integrate import solve_ivp

# Definimos la ecuación diferencial
def f(t, y):
    return [y[1], -2*y[1] - y[0]]

# Condiciones iniciales
y0 = [0, 1]

# Intervalo de tiempo a considerar
t_span = [0, 10]

# Resolución de la ecuación diferencial
solucion = solve_ivp(f, t_span, y0)

# Resultado
print(solucion.y)

Este código resuelve una ecuación diferencial de segundo orden utilizando la función solve_ivp de la biblioteca SciPy.

Primero se define la ecuación diferencial a resolver en la función f, donde se especifica la derivada de la función y con respecto a t. En este caso, se trata de una ecuación diferencial de segundo orden de la forma y'' + 2y' + y = 0.

Luego se especifican las condiciones iniciales y0 para la función y y el intervalo de tiempo t_span en el que se desea resolver la ecuación diferencial.

Finalmente, se utiliza la función solve_ivp para resolver la ecuación diferencial con los parámetros especificados, y se almacena la solución en la variable solucion. Se imprime el resultado de la solución y en cada punto en el intervalo de tiempo especificado.

La solución devuelta será una matriz de dos filas, una para cada variable en el sistema de ecuaciones diferenciales.

Optimización con NumPy y SciPy: Ejemplo práctico de Maximización de Beneficios.

En economía, una función de producción describe la relación entre los insumos (factores productivos) y la cantidad de producto que una empresa puede producir utilizando esos insumos. Básicamente, es una fórmula que nos dice cuánta producción se puede obtener con diferentes combinaciones de trabajo, capital y otros insumos.

Los insumos son los recursos que una empresa utiliza para producir bienes o servicios. Los insumos más comunes son el trabajo (es decir, el tiempo y la energía que las personas dedican a la producción) y el capital (es decir, las herramientas, maquinaria y edificios que se utilizan en el proceso productivo).

La función de producción es importante porque permite modelar cómo los cambios a las cantidades de insumos afecta la cantidad de producción. Por ejemplo, si se aumenta la cantidad de trabajo, ¿cómo afectará esto a la cantidad de producción? ¿Cuánto capital es necesario para producir una cantidad determinada de producción?

Un ejemplo imaginario para entender la optimización

Veremos que en este ejemplo hipotético, la empresa no puede gastar más de $300 para adquirir el capital y trabajo para su proceso de producción (la restricción presupuestaria). En otras palabras, la restricción presupuestaria se define como el costo total de contratar trabajadores (4L) y unidades de capital (6K), que no puede superar los $300.

Es lógico pensar que $300 es muy poco para poner en marcha un proceso productivo, y ¡estamos en lo cierto! Pero en este caso solo queremos analizar la optimización en SciPy por lo que está simplificado al máximo. Si aún te parece un ejemplo "chocante"; podemos pensar que es una pequeña fábrica y que la producción es por hora.

Por otra parte; la función de beneficios se define como la diferencia entre los ingresos generados por la producción y los costos de los inputs (4L y 6K).

Buscamos la combinación de trabajo y capital que maximicen la producción los beneficios de esta empresa, teniendo en cuenta la restricción presupuestaria.

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# Definimos la función de producción
def funcion_produccion(inputs):
    L, K = inputs
    return (L**(1/2)) * (K**(1/2))

# Definimos la función de beneficios
def funcion_beneficios(inputs):
    return 10 * funcion_produccion(inputs) - 4 * inputs[0] - 6 * inputs[1]

# Definimos la restricción presupuestaria
def restriccion_presupuestaria(inputs):
    return 4 * inputs[0] + 6 * inputs[1] - 300

# Encontramos los inputs óptimos sujetos a la restricción presupuestaria
guess_inicial = [1, 1]
resultado = minimize(lambda x: -funcion_beneficios(x), guess_inicial, constraints=[{'type': 'eq', 'fun': restriccion_presupuestaria}])
inputs_optimos = resultado.x

# Calculamos la producción y los beneficios óptimos
produccion_optima = funcion_produccion(inputs_optimos)
beneficios_optimos = funcion_beneficios(inputs_optimos)

# Graficamos la función de producción
valores_L = np.linspace(0, 100, 100)
valores_K = np.linspace(0, 100, 100)
L_mesh, K_mesh = np.meshgrid(valores_L, valores_K)
Q_mesh = funcion_produccion([L_mesh, K_mesh])
fig, ax = plt.subplots()
ax.set_xlabel('Trabajo (L)')
ax.set_ylabel('Capital (K)')
ax.set_title('Función de producción')
ax.contour(L_mesh, K_mesh, Q_mesh, levels=10)
ax.plot(inputs_optimos[0], inputs_optimos[1], 'ro', label='Punto óptimo')
ax.legend()

plt.show()

# Imprimimos los resultados
print(f"Inputs óptimos: {inputs_optimos}")
print(f"Producción óptima: {produccion_optima}")
print(f"Beneficios óptimos: {beneficios_optimos}")

#Resultado
Inputs óptimos: [37.49974611 25.00016926]
Producción óptima: 30.618621784087956
Beneficios óptimos: 6.186217840879607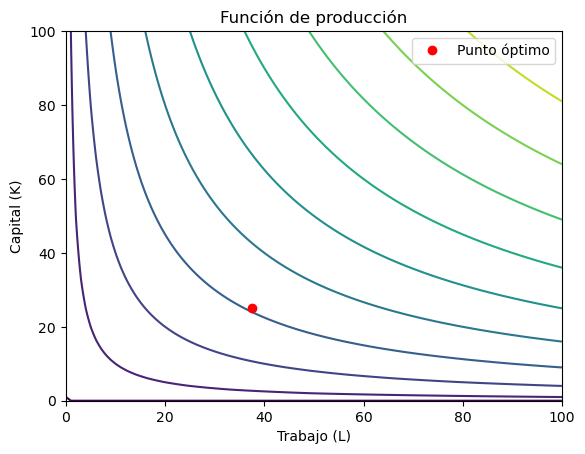

Explicación de los resultados

Los resultados indican que la empresa debería utilizar aproximadamente 37 unidades de trabajo (L) y 25 unidades de capital (K) por hora para obtener la máxima producción y beneficios. Con estos inputs óptimos, la producción óptima es de aproximadamente 31 unidades por hora, mientras que los beneficios óptimos son de 6.19 dólares por hora.

Es decir, que si la empresa utiliza en promedio 37 unidades de trabajo y 25 de capital; obtendrá $6.19 de beneficios por cada $300 invertidos en capital y trabajo.

También podemos interpretar los resultados gráficamente a partir del gráfico de la función de producción. El punto óptimo, representado por un círculo rojo, se encuentra en el lugar donde las curvas de nivel de la función de producción son tangentes a la restricción presupuestaria.

En este punto, la pendiente de la curva de nivel de la función de producción coincide con la pendiente de la recta presupuestaria, lo que indica que la empresa está utilizando de manera eficiente sus recursos para maximizar sus beneficios.

Nuestro ejercicio resuelve un problema de optimización en el que una empresa hipotética desea maximizar sus beneficios al elegir la cantidad óptima de dos factores de producción: trabajo y capital.

La empresa está limitada por un presupuesto dado, es decir, no puede gastar más dinero del que tiene disponible, y además tiene una función de producción que describe cómo la cantidad de trabajo y capital utilizada afecta la cantidad producida.

El objetivo de la empresa es determinar la cantidad óptima de trabajo y capital para maximizar sus beneficios, dada la restricción presupuestaria y la función de producción. Para resolver este problema, utilizamos la biblioteca SciPy que proporciona herramientas para la optimización numérica.

Dado que el enfoque de este artículo es en la programación no entraremos en los detalles de la microeconomía (Función Cobb Douglas, isocuantas, rendimientos constantes a escala etc). Ten en cuenta que este ejercicio es un ejemplo grosso modo, de las capacidades de SciPy y que pudieramos agregar mucho más.

En nuestro código tenemos definida la función de producción, la función de beneficios y la restricción presupuestaria en términos matemáticos. Luego utilizamos la función minimize de SciPy para encontrar la combinación óptima de trabajo y capital que maximiza los beneficios de la empresa, sujeto a la restricción presupuestaria.

Finalmente, el código grafica la función de producción para visualizar la combinación óptima de trabajo y capital, y muestra los resultados óptimos de producción, beneficios y los inputs óptimos.

Palabras finales y recomendaciones.

Hemos llegado al final de este artículo. Si llegaste hasta aquí, muchísimas gracias por leer. En este artículo hemos cubierto algunas de las aplicaciones de SciPy y NumPy al cálculo scientífico.

Aún así, esto solo es una pequeña presentación de un campo de aplicación muchísimo más vasto. Aún así, espero haya sido de relevancia y utilidad.

Quisiera cerrar esta guía con 3 conclusiones/recomendaciones al respecto. Debido a que NumPy es un poco más popular, me centraré más en SciPy:

1. SciPy es la biblioteca de Python más utilizada para el análisis científico y matemático además de tener las características de optimización más potentes. A su vez destaca por su facilidad de usar para resolver problemas complejos.
2. Si bien hay muchas bibliotecas mucho más populares que SciPy, entre los científicos de datos y profesiones afines; lo cierto es que recomiendo aprender un poco de SciPy, o por lo menos ver algunos proyectos para tener una idea general. En lo personal considero que esta biblioteca ayuda a desarrollar el planteamiento y resolución de problemas así como el pensamiento sistémico.

A diferencia de Matplotlib o Pandas, en donde puedes pensar que ya sabes más o menos "cómo hacer lo que quieres hacer"; en SciPy necesitas plantear primero el problema y después estructurar el código.

1. En este artículo se introdujeron SciPy y NumPy juntos, pero no es que sea inseparables o algo por el estilo, la asociación fue por motivos pedagógicos. Lo cierto es que puedes integrar SciPy y NumPy cada vez que necesites un cálculo específico en tus proyectos, de hecho muy a menudo tienen el papel de simples "calculadoras" más que de protagonistas.

En otras palabras; estas bibliotecas no son una especie de "campo de estudio" o algo "exhaustivo" que hay que dominar, aunque ciertamente te pueden facilitar la vida en tu camino hacia la programación.

Nuevamente, muchas gracias por leer, y si te interesa aprender más acerca del cálculo científico en Python, freeCodeCamp ofrece una certificación en detalle. Te deseo lo mejor y, ¡Feliz Programación!