En ciencias de la computación, el análisis de algoritmos es una parte muy importante. Es importante buscar el algoritmo más eficiente para resolver un problema. Es posible tener muchos algoritmos para resolver un problema, el reto es elegir el más eficiente.
Ahora el punto es, ¿Cómo podemos reconocer el algoritmo más eficiente si tenemos un conjunto de algoritmos diferentes? Aquí, es donde surge el concepto de complejidad espacial y temporal de los algoritmos. La complejidad espacial y temporal actúa como escala de medición de los algoritmos. Comparamos los algoritmos en función de su complejidad espacial (cantidad de memoria) y temporal (número de operaciones).
La cantidad total de memoria del ordenador utilizada cuando se ejecuta es la complejidad espacial de ese algoritmo. No hablaremos de dicha complejidad en este artículo (para hacer este artículo más pequeño).
Complejidad temporal
La complejidad temporal es el número de operaciones que realiza un algoritmo para completar su tarea (considerando que cada operación dura el mismo tiempo). El algoritmo que realiza la tarea en el menor número de operaciones se considera el más eficiente en términos de complejidad temporal. Sin embargo, la complejidad espacial y temporal se ve afectada por factores como el sistema operativo y el hardware, pero no los incluiremos en discusión.
Ahora para entender la complejidad temporal, tomaremos un ejemplo en el que compararemos dos algoritmos diferentes que se utilizan para resolver un problema concreto.
El problema es la búsqueda. Tenemos que buscar un elemento en un arreglo (en este problema, vamos a suponer que el arreglo está ordenado de forma ascendente). Para resolver el problema tenemos dos algoritmos:
1. Búsqueda lineal.
2. Búsqueda binaria.
Tomemos como ejemplo un arreglo con diez elementos, y tenemos que encontrar el número diez en el arreglo.
const arreglo = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
const digito_buscado = 10;El algoritmo de búsqueda lineal comparará cada elemento del arreglo con digito_buscado. Cuando encuentre el digito_buscado en el arreglo regresara true.
Ahora vamos a contar el número de operaciones que realiza. En este caso, la respuesta es 10 (ya que compara cada elemento del arreglo). Entonces la búsqueda lineal utiliza diez operaciones para encontrar el elemento dado (este es el número máximo de operaciones para este arreglo; este caso también es conocido como el peor caso de un algoritmo).
En general la búsqueda lineal tardará un número n de operaciones en su peor caso (donde n es el tamaño del arreglo).
Analizaremos el algoritmo de búsqueda binaria para este caso.
La búsqueda binaria puede entenderse fácilmente con este ejemplo:
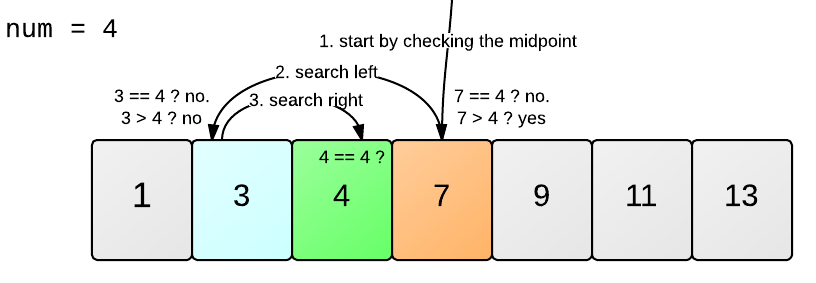
Fuente: Learneroo
Si intentamos aplicar esta lógica en nuestro problema entonces, primero compararemos digito_buscado con el elemento central del arreglo, es decir 5. Ahora como 5 es menor que 10, entonces empezaremos a buscar el digito_buscado en los elementos del arreglo mayores que 5, de la misma manera hasta que obtengamos el elemento deseado 10.
Ahora, intenta contar el número de operaciones que la búsqueda binaria ha necesitado para encontrar el elemento deseado. Se necesitaron aproximadamente cuatro operaciones. Este fue el peor caso de la búsqueda binaria. Esto demuestra que existe una relación logarítmica entre el número de operaciones realizadas y el tamaño total del arreglo.
número de operaciones = log(10) = 4 (aprox.)
para la base 2
Podemos generalizar este resultado para la búsqueda binaria como:
Para un arreglo de tamaño n, el número de operaciones realizadas por la búsqueda binaria es: log(n)
La notación Big O
En las afirmaciones anteriores, vimos que para un arreglo de tamaño n, la búsqueda lineal realizara n operaciones para completar la búsqueda. Por otro lado, la búsqueda binaria realiza un número log(n) de operaciones (ambas para sus peores casos). Podemos representar esto con una gráfica (eje-x: número de elementos, eje-y: número de operaciones).
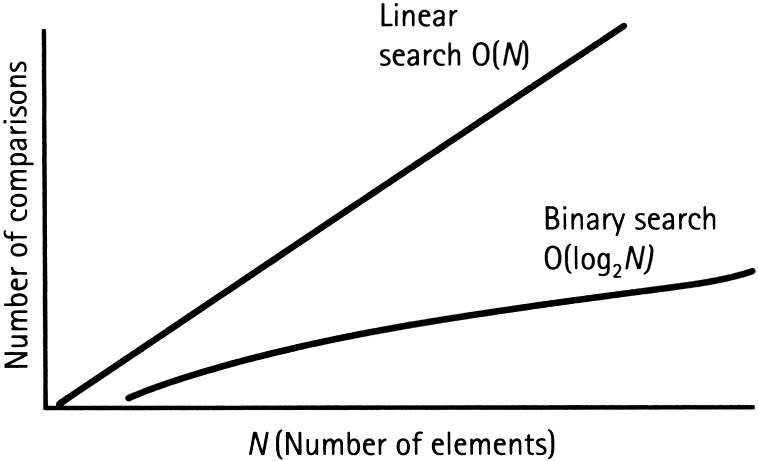
Fuente: Techtud
En la figura se puede observar claramente que el ritmo de aumento de la complejidad de la búsqueda lineal es mucho más rápido que el de la búsqueda binaria.
Cuando analizamos un algoritmo, utilizamos una notación para representar su complejidad temporal y esa notación es llamada Big O.
Por ejemplo: la complejidad temporal para la búsqueda lineal puede representarse como O(n) y O(log n) para la búsqueda binaria (donde n y log(n) son el número de operaciones).
La complejidad temporal o las notaciones Big O para algunos algoritmos populares se enumeran a continuación:
- Búsqueda binaria: O(log n)
- Búsqueda lineal: O(n)
- Ordenamiento rápido (Quick Sort): O(n * log n)
- Ordenamiento por selección: O(n * n)
- Problema del viajero: O(n!)
Conclusión
Aprecio mucho su esfuerzo si todavía está leyendo este artículo. Ahora, debes estar pensando: ¿Por qué es tan importante entender la complejidad temporal de un algoritmo?
Sabemos que para un número pequeño de elementos (digamos 10), la diferencia entre el número de operaciones realizadas por la búsqueda binaria y la búsqueda lineal no es tan grande. Pero en el mundo real, la mayoría de las veces, nos enfrentamos a problemas que tienen una enorme cantidad de datos.
Por ejemplo, si tenemos 4 billones de elementos que buscar, en el peor de los casos la búsqueda lineal tardara 4 billones de operaciones en completar su tarea. La búsqueda binaria completará esta tarea en solo 32 operaciones. Es una gran diferencia. Ahora supongamos que si una operación tarda 1 ms en completarse, entonces la búsqueda binaria tardara solo 32 ms mientras que la búsqueda lineal tardara 4 billones ms (es decir, unos 46 días). Es una diferencia significativa.
Por este motivo, el estudio de la complejidad temporal adquiere importancia cuando se trata de una cantidad de datos muy grande.
Traducido del artículo de Aditya Dehal - An Introduction to the Time Complexity of Algorithms

