Articolo originale: What is Big O Notation Explained: Space and Time Complexity
Sai davvero cos'è la notazione O grande? Se lo sai, allora questo sarà un ripasso in previsione di un colloquio di lavoro. In caso contrario, non preoccuparti – unisciti a me in questo viaggio nell'informatica.
Se hai frequentato dei corsi riguardanti gli algoritmi, hai probabilmente sentito il termine notazione O grande. Se non ne hai mai sentito parlare, lo faremo a breve, per poi raggiugere un comprensione più approfondita di cosa è realmente.
La notazione O grande è uno degli strumenti fondamentali a disposizione degli informatici, così come per gli ingegneri del software, per analizzare il costo di un algoritmo.
Questo articolo è scritto con il presupposto che tu abbia già avuto a che fare con del codice. Inoltre, alcuni materiali approfonditi richiedono conoscenze di base di matematica a livello di scuola superiore, quindi possono essere poco adatti a principianti assoluti. Ma sei ti senti pronto, iniziamo!
In questo articolo, avremo una discussione approfondita riguardo alla notazione O grande. Inizieremo con un esempio di algoritmo per iniziare a capirne qualcosa. Poi passeremo alla matematica per ottenere una comprensione più formale. In seguito parleremo di alcune variazioni comuni di notazione O grande. Alle fine discuteremo di alcune limitazioni di O grande in situazioni pratiche. Di seguito è possibile vedere un sommario.
Sommario
- Cos'è la notazione O grande e perché è importante
- Definizione formale di notazione O grande
- O grande, o piccola, Omega e Theta
- Confronto di complessità tra valori tipici di O grande
- Complessità temporale e spaziale
- Complessità attesa, caso migliore, medio e peggiore
- Perché O grande non conta
- In conclusione…
Iniziamo!
1. Cos'è la notazione O grande e perché è importante
“La notazione O grande è una notazione matematica che descrive il comportamento asintotico di una funzione quando l'argomento tende a un particolare valore o a infinito. È un membro della famiglia di notazioni inventate da Paul Bachmann, Edmund Landau e altri, collettivamente chiamate notazione Bachmann–Landau o notazione asintotica.”
— Definizione di notazione O grande da Wikipedia
In parole povere, la notazione O grande descrive la complessità di un codice usando termini algebrici.
Per capire cos'è la notazione O grande, possiamo dare un'occhiata a un tipico esempio, O(n²). La lettera “n” rappresenta la dimensione dell'input e la funzione “g(n) = n²” all'interno di “O()” ci dà un'idea di quanto sia complesso l'algoritmo rispetto alla dimensione dell'input.
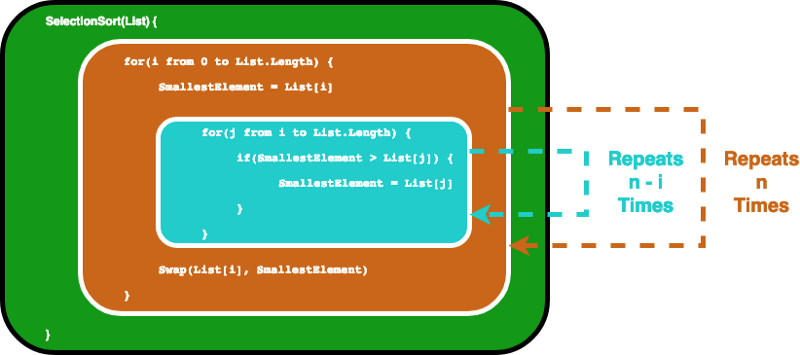
Un tipico algoritmo con complessità pari a O(n²) è l'algoritmo selection sort, un algoritmo di ordinamento che itera su una lista per assicurare che ogni elemento all'indice i sia l'i-esimo elemento più piccolo/grande della lista. Il CODEPEN qui sotto fornisce un esempio visuale.
L'algoritmo può essere descritto con il seguente codice. Per assicurare che l'elemento i-esimo sia l'i-esimo elemento più piccolo nella lista (indicato come SmallestElement nello snippet di codice seguente), questo algoritmo itera prima sulla lista con un loop for. Poi, per ogni elemento utilizza un altro loop per trovare l'elemento più piccolo nella parte restante della lista.
SelectionSort(List) {
for(i from 0 to List.Length) {
SmallestElement = List[i]
for(j from i to List.Length) {
if(SmallestElement > List[j]) {
SmallestElement = List[j]
}
}
Swap(List[i], SmallestElement)
}
}In questa situazione, consideriamo la variabile List come input, dunque la dimensione dell'input n è il numero di elementi all'interno di List. Assumendo che l'istruzione if e l'assegnazione del valore legata all'istruzione if necessiti di un tempo costante, possiamo trovare la notazione O grande per la funzione SelectionSort analizzando quante volte vengono eseguite le istruzioni.
Le istruzioni nel loop interno vengono eseguite n volte. Dopo che i viene incrementata, il loop interno viene eseguito n-1 volte, e così via finché non viene eseguito una volta, prima che entrambi i loop for raggiungano le condizioni di terminazione.
Alla fine ci ritroviamo con la somma di una serie geometrica, e con un po' di matematica da scuole superiori possiamo trovare che il loop interno viene ripetuto 1 + 2... + n volte, ovvero n(n-1)/2 volte. Moltiplicando otteniamo n²/2-n/2.
Quando calcoliamo la notazione O grande ci interessiamo solo dei termini dominanti, senza curarci dei coefficienti. Quindi, prendiamo n² come O grande finale e scriviamo O(n²).
Ora potresti chiederti perché si riduce tutto al “termine dominante” e perché non ci interessiamo dei coefficienti. Non preoccuparti, affronteremo questi aspetti uno alla volta. Potrebbe essere un po' difficile da capire all'inizio ma diventerà tutto più sensato man mano che leggerai la prossima sezione.
2. Definizione formale di notazione O grande
C'era una volta un re indiano che voleva ricompensare un uomo saggio per la sua bravura. Il saggio chiese nient'altro che il grano che potesse riempire una scacchiera.
Ma queste erano le sue regole: nella prima casella voleva 1 chicco di grano, poi 2 nella seconda casella, 4 nella successiva e così via, in modo che ogni casella della scacchiera fosse riempita con una quantità di grano pari al doppio della precedente. Il re ingenuo acconsentì senza esitazione, pensando che sarebbe stata una domanda banale da soddisfare, finché non provò a farlo...

Quindi, quanti chicchi di grano doveva il re al saggio? Sappiamo che una scacchiera contiene 8 caselle per 8 caselle, per un totale di 64, dunque la casella finale dovrebbe contenere un totale di 2⁶³ chicchi di grano. Se fai il calcolo, otterrai 1.8446744*10¹⁹, ovvero circa 18 seguito da 18 zeri. Assumendo che ogni chicco di grano pesi 0.01 grammi, il totale è 184,467,440,737 tonnellate di grano. E 184 miliardi di tonnellate sono parecchie, non è vero?
Da un certo punto, i numeri crescono piuttosto velocemente per via dell'andamento esponenziale. La stessa logica vale per gli algoritmi informatici. Se l'impegno richiesto per svolgere un'azione cresce esponenzialmente con la dimensione dell'input, può finire per diventare estremamente grande.
Come vedremo a breve, la crescita di 2ⁿ è molto più rapida rispetto a n². Con n = 64, il quadrato di 64 è 4096. Se aggiungi questo numero a 2⁶⁴, verrà perso al di fuori delle cifre significative.
Ecco perché, quando ci interessa la velocità di crescita, ci concentriamo sui termini dominanti. E dato che vogliamo analizzare la crescita rispetto alle dimensioni dell'input, i coefficienti che moltiplicano solo il numero, piuttosto che crescere con le dimensioni dell'input, non contengono informazioni utili.
Qui sotto puoi vedere la definizione formale di O grande:
f(N) = O(g(N)), se esistono costanti positive c, N0 tali che
f(N) ≤ c · g(N) per ogni N ≥ N0
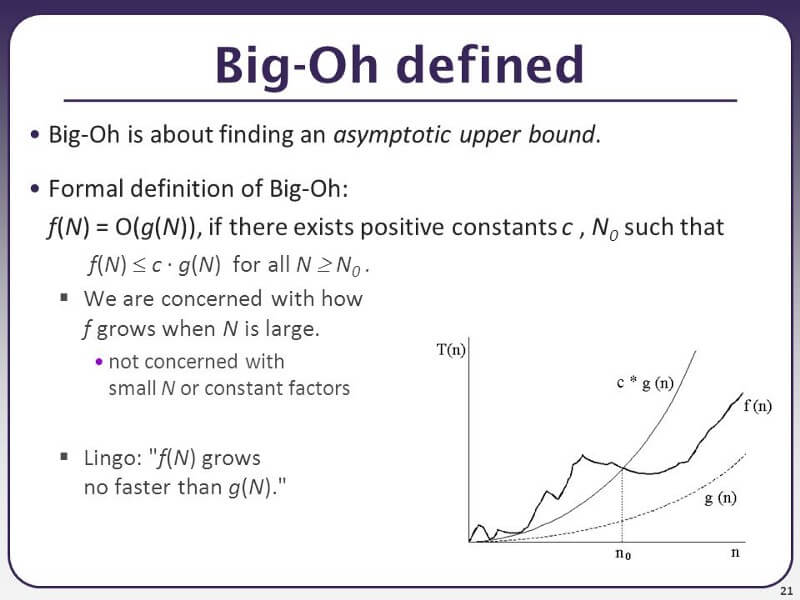
La definizione formale è utile quando devi svolgere una prova di matematica. Ad esempio, la complessità temporale di selection sort può essere definita dalla funzione f(n) = n²/2-n/2, come abbiamo discusso nella sezione precedente.
Se la nostra funzione g(n) è n², possiamo trovare una costante c = 1 e una N₀ = 0, e finché N > N₀, N² sarà sempre più grande di N²/2-N/2. Possiamo provarlo facilmente sottraendo N²/2 da entrambe le funzioni, poi possiamo vedere facilmente che N²/2 > -N/2 è vero quando N > 0. Dunque, possiamo giungere alla conclusione che f(n) = O(n²).
Potresti aver notato un piccolo trucchetto qui. Ovvero, se g(n) cresce velocemente, molto più veloce di qualsiasi cosa, O(g(n)) sarà sempre abbastanza grande. Ad esempio, per una funzione polinomiale, puoi avere sempre ragione dicendo che è O(2ⁿ) perché 2ⁿ alla fine supererà qualsiasi polinomio.
Matematicamente è corretto, ma in generale, quando parli di O grande, occorre conoscere l'estremo della funzione. Ne capirai di più leggendo la prossima sezione.
Ma prima di andare avanti, testiamo la tua comprensione con la seguente domanda. La risposta può essere trovata nelle sezioni successive.
Domanda: un'immagine è rappresentata da un array 2D di pixel. Se utilizzi un loop for annidato per iterare su ogni pixel (ovvero, hai un loop for che itera su tutte le colonne e un altro loop for che itera su tutte le righe), qual è la complessità temporale dell'algoritmo quando l'immagine è considerata come input?
3. O grande, o piccola, Omega e Theta
O grande: “f(n) è O(g(n))” se e solo se per delle costanti c e N₀, f(N) ≤ cg(N) per ogni N > N₀
Omega: “f(n) è Ω(g(n))” se e solo se per delle costanti c e N₀, f(N) ≥ cg(N) per ogni N > N₀
Theta: “f(n) è Θ(g(n))” se e solo se f(n) è O(g(n)) e f(n) è Ω(g(n))
o piccola: “f(n) è o(g(n))” se e solo se f(n) è O(g(n)) e f(n) non è Θ(g(n))
— Definizione formale di O grande, omega, theta e o piccola
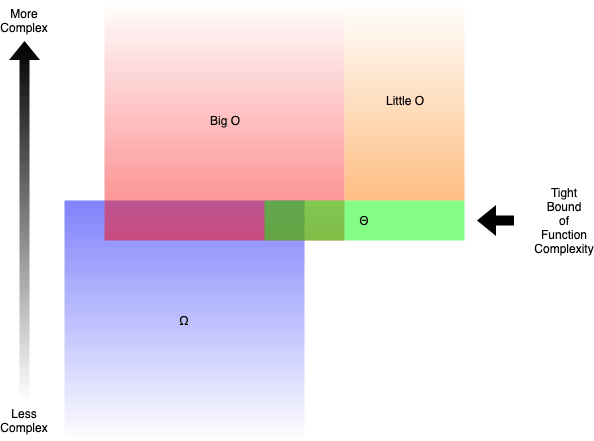
In parole povere:
- O grande (O()) descrive il limite superiore della complessità.
- Omega (Ω()) descrive il limite inferiore della complessità.
- Theta (Θ()) descrive il limite asintotico stretto della complessità.
- o piccola (o()) descrive il limite superiore escludendo il limite stretto.
Ad esempio, la funzione g(n) = n² + 3n è O(n³), o(n⁴), Θ(n²) e Ω(n). Ma sarebbe ancora corretto se dicessi che è Ω(n²) oppure O(n²).
In generale, quando parliamo di O grande, ciò intendiamo in realtà è theta. È piuttosto insensato quando il limite superiore è molto più grande dell'ambito dell'analisi. Sarebbe un po' come risolvere diseguaglianze mettendo ∞ dal lato più grande, cosa che ti farebbe avere ragione praticamente quasi sempre.
Ma come determiniamo quali funzioni sono più complesse di altre? Lo scoprirai nella prossima sezione e imparandolo nel dettaglio.
4. Confronto di complessità tra valori tipici di O grande
Se tentiamo di calcolare la O grande per una particolare funzione g(n), ci interessa solo il termine dominante della funzione. Il termine dominante è il termine che cresce più velocemente.
Ad esempio, n² cresce più velocemente di n, quindi se abbiamo qualcosa come g(n) = n² + 5n + 6, sarà O(n²). Se hai seguito qualche corso di analisi, tutto ciò è molto simile alla scorciatoia per trovare il limite per polinomi frazionari, dove alla fine ti interessa solo il termine dominante per numeratori e denominatori.

Ma quale funzione cresce più velocemente delle altre? Per determinarlo esistono alcune regole.
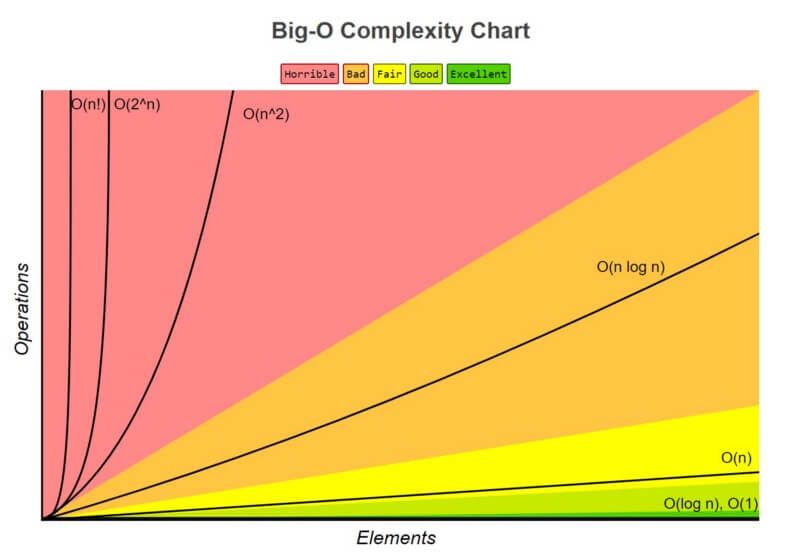
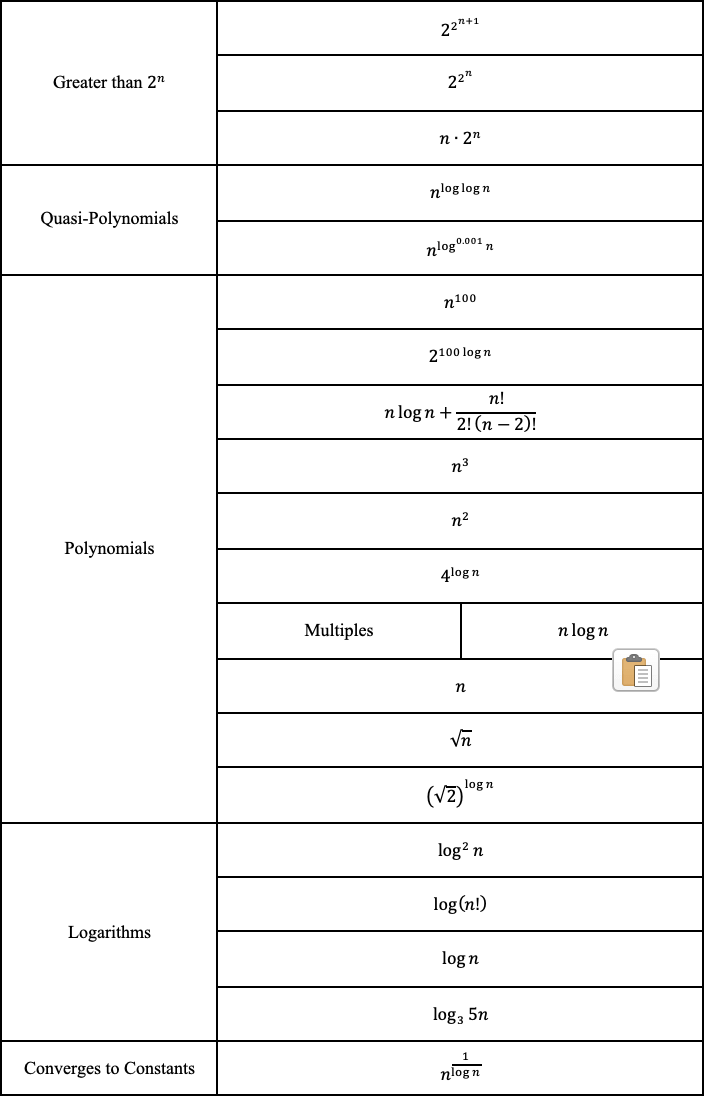
1. O(1) ha la complessità minore
Spesso chiamato "tempo costante", se crei un algoritmo che risolve un problema in O(1), sei probabilmente al massimo delle tue possibilità. In alcuni casi, la complessità può andare oltre O(1), e puoi analizzarli trovando la sua controparte O(1/g(n)). Ad esempio, O(1/n) è più complessa di O(1/n²).
2. O(log(n)) è più complessa di O(1), ma meno complessa dei polinomi
Dato che la complessità è spesso correlata agli algoritmi divide et impera, O(log(n)) è generalmente una buona complessità da raggiungere con gli algoritmi di ordinamento. O(log(n)) è meno complessa di O(√n), perché la radice quadrata può essere considerata polinomiale, dove l'esponente è 0.5.
3. La complessità dei polinomi cresce con il loro esponente
Ad esempio, O(n⁵) è più complessa di O(n⁴). Grazie a questa semplicità, abbiamo fatto svariati esempi di polinomi nelle sezioni precedenti.
4. Le funzioni esponenziali hanno una complessità maggiore delle polinomiali finché i coefficienti sono multipli positivi di n
O(2ⁿ) è più complesso di O(n⁹⁹), ma O(2ⁿ) è meno complesso di O(1). Generalmente, prendiamo 2 come base per gli esponenziali e i logaritmi perché le cose tendono a essere binarie in informatica, ma gli esponenti possono essere cambiati variando i coefficienti. Quando non specificato, la base dei logaritmi è 2.
5. I fattoriali hanno una complessità maggiore delle esponenziali
Se ti interessa il ragionamento, dai un'occhiata alla funzione gamma, una continuazione analitica di un fattoriale. Una breve dimostrazione è che sia fattoriali che esponenziali hanno lo stesso numero di moltiplicazioni, ma il numero che viene moltiplicato cresce per i fattoriali, mentre rimane costante per gli esponenziali.
6. Moltiplicare i termini
Moltiplicando, la complessità sarà maggiore di quella originale, ma non più grande del prodotto ottenuto moltiplicando qualcosa di più complesso. Ad esempio, O(n * log(n)) è più complessa di O(n) ma meno complessa di O(n²), perché O(n²) = O(n * n) e n è più complessa di log(n).
Per metterti alla prova, cerca di ordinare le seguenti funzioni dalla più complessa alla meno complessa. Continuando a leggere potrai trovare la soluzione con spiegazioni dettagliate in una sezione successiva. Alcune sono scelte per essere ingannevoli e potrebbero richiedere conoscenze matematiche approfondite. Man mano che ti avvicini alla soluzione capirai meglio.
Domanda: ordina le seguenti funzioni dalla più complessa alla meno complessa.
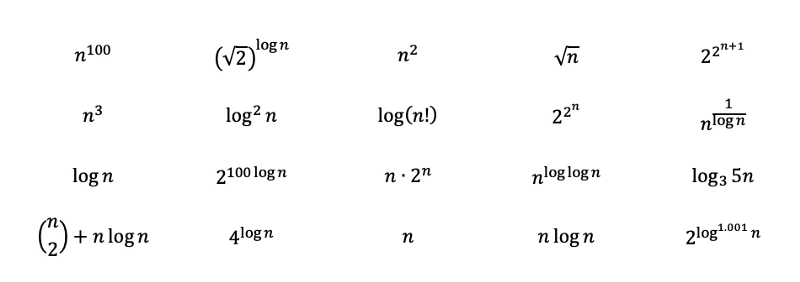
Soluzione alla domanda della sezione 2:
Era volontariamente ideata in modo da essere una domanda insidiosa per metterti alla prova. La domanda ti tenta a rispondere O(n²) perché c'è un loop annidato. Tuttavia, n è la dimensione dell'input. Dato che l'array dell'immagine è l'input e il loop itera su ogni pixel solo una volta, la risposta in realtà è O(n). Nella prossima sezione ci saranno più esempi come questo.
5. Complessità temporale & spaziale
Finora, abbiamo parlato solo della complessità temporale degli algoritmi, ovvero ci siamo interessati solo al tempo che impiega il programma per completare l'attività. Ma ciò che conta è anche lo spazio che il programma necessita per completare l'attività. La complessità spaziale è correlata a quanta memoria userà il programma, dunque un altro fattore importante da analizzare.
La complessità spaziale funziona in modo simile alla complessità temporale. Ad esempio, selection sort ha una complessità spaziale di O(1), perché memorizza soltanto un valore minimo e il suo indice come confronto, e lo spazio massimo utilizzato non cresce con la dimensione dell'input.
Alcuni algoritmi, come bucket sort, hanno una complessità spaziale di O(n), ma sono in grado di ridurre la complessità temporale fino a O(1). Bucket sort ordina l'array creando una lista ordinata di tutti i possibili elementi nell'array, poi incrementa il conteggio ogni volta che incontra un elemento. Alla fine, l'array ordinato sarà la lista ordinata di elementi ripetuti a seconda del loro conteggio.
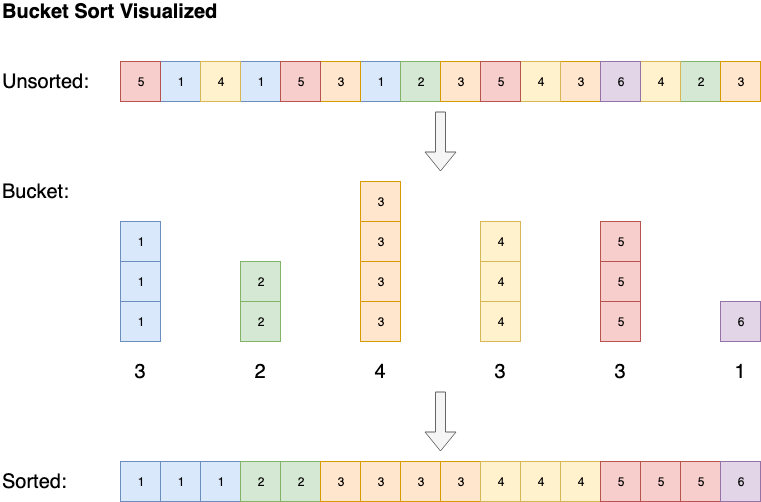
6. Complessità attesa, caso migliore, medio e peggiore
La complessità può anche essere analizzata secondo caso migliore, peggiore, medio e caso atteso
Prendiamo come esempio insertion sort. L'algoritmo itera su tutti gli elementi nella lista. Se un elemento è minore del precedente, lo inserisce indietro, finché non è maggiore dell'elemento che lo precede.
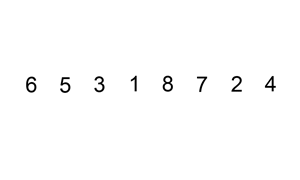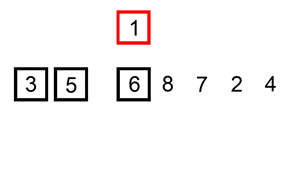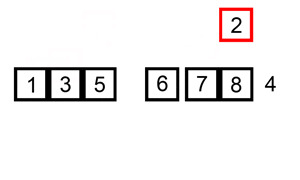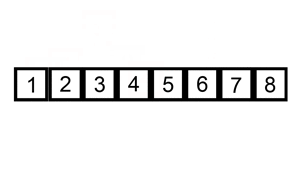
Se l'array è inizialmente ordinato, non verrà effettuato nessuno scambio. L'algoritmo itererà semplicemente sugli elementi dell'array una volta, ottenendo una complessità di O(n). Dunque, possiamo dire che il caso migliore di complessità temporale di insertion sort è O(n). Una complessità di O(n) è spesso chiamata complessità lineare.
A volte un algoritmo è sfortunato. Quick sort, ad esempio, dovrà scorrere attraverso la lista in un tempo O(n) se gli elementi sono ordinati nel verso opposto, ma in media ordina un array in un tempo O(n * log(n)). Generalmente, quando valutiamo la complessità di un algoritmo, ci interessiamo alle prestazioni nel caso peggiore. Parleremo ancora di questo e di quick sort nella prossima sezione.
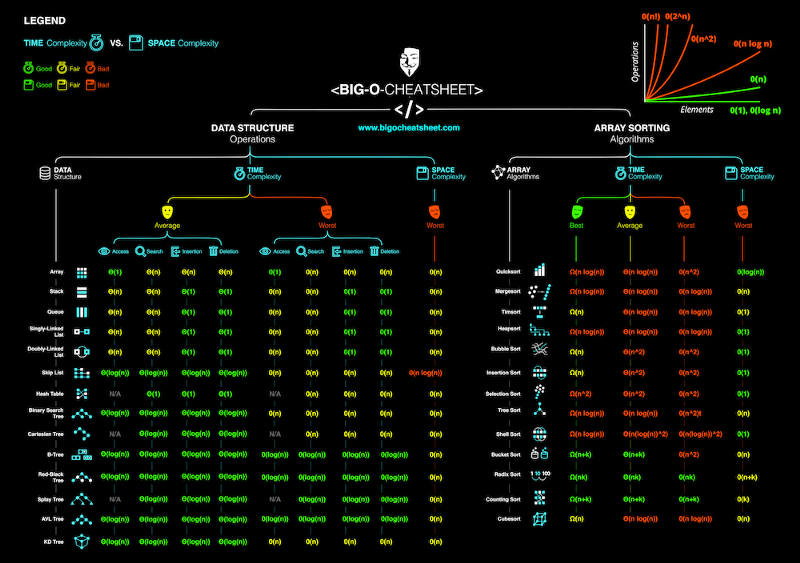
La complessità del caso medio descrive la prestazione attesa da un algoritmo. A volte implica il calcolo della probabilità di ogni situazione. Può diventare complicato addentrarsi nei dettagli e perciò non ne discuterò in questo articolo. Qui sotto puoi trovare uno specchietto riassuntivo sulle complessità spaziali e temporali di algoritmi tipici.
Soluzione alla domanda della sezione 4:
Analizzando le funzioni, dovremmo essere in grado di classificare immediatamente i seguenti polinomi dal più complesso al meno complesso con la regola 3. Dove la radice quadrata di n corrisponde semplicemente all'elevamento all'esponente 0.5.
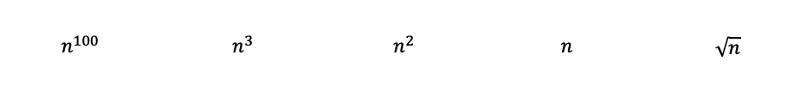
Poi, applicando le regole 2 e 6, otteniamo quanto segue. Il logaritmo in base 3 può essere trasformato in base 2 con un cambiamento di base. Il logaritmo in base 3 cresce un po' più lentamente di quelli in base 2 e quindi viene posizionato dopo.
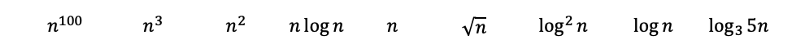
Il resto potrebbe sembrare un po' complicato, ma tentiamo di svelare l'arcano e vedere dove possiamo inserire le funzioni rimanenti.
Prima di tutto, 2 elevato a 2 alla n è maggiore di 2 alla n, e il +1 concorre a un aumento ulteriore.

E dato che sappiamo che 2 elevato a log(n) in base 2 è uguale a n, possiamo convertire le seguenti funzioni. Il logaritmo con esponente 0.001 cresce un po' di più di una costante, ma meno di quasi ogni altra cosa.

La funzione con n alla potenza di log(log(n)), in realtà è una variazione della quasi-polinomiale, che è maggiore della polinomiale ma minore dell'esponenziale. Dato che log(n) cresce più lentamente di n, la complessità è leggermente inferiore. La funzione con il reciproco del logaritmo converge a una costante, dato che 1/log(n) diverge verso infinito.

I fattoriali possono essere rappresentati con delle moltiplicazioni e quindi possono essere convertiti in addizioni fuori dalla funzione logaritmica. "n su 2" può essere convertito in un polinomio con il termine più grande cubico.

E finalmente, possiamo ordinare le funzioni dalla più complessa alla meno complessa.
Perché O grande non conta
!!! — ATTENZIONE — !!!
I contenuti discussi qui, non sono generalmente accettati dalla maggior parte dei programmatori nel mondo. Parlane a tuo rischio durante un colloquio. Alcune persone riportano che hanno fallito il loro colloquio di lavoro perché hanno messo in discussione l'autorità, come qui.
!!! — ATTENZIONE — !!!
Dato che abbiamo precedentemente imparato che il caso peggiore di complessità temporale per quick sort è O(n²), mentre per merge sort è O(n * log(n)), merge sort dovrebbe essere più veloce, vero? Hai probabilmente indovinato che la risposta è falso.
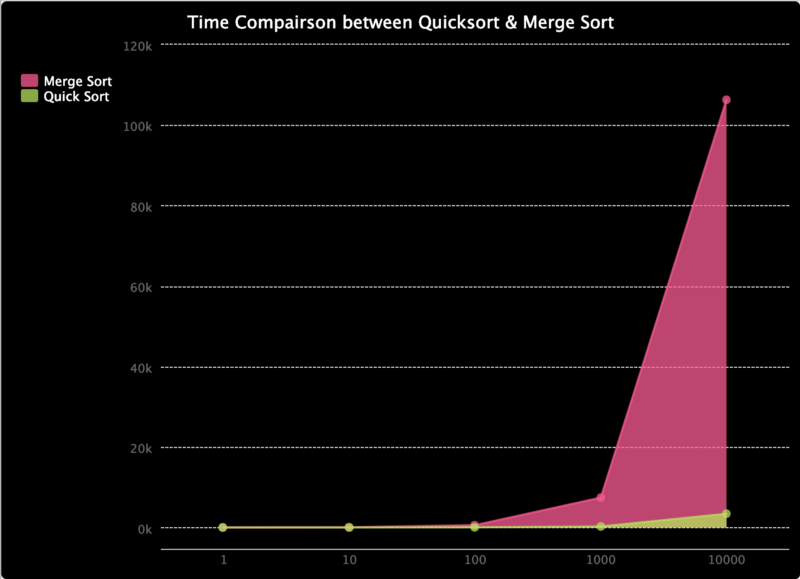
Per dimostrarlo, dai un'occhiata a questo trinket.io che ho realizzato. Confronta il tempo per quick sort e merge sort. L'ho testato solo su array con una lunghezza fino a 10000, ma come puoi vedere, il tempo per merge sort cresce più velocemente che per quick sort. Nonostante quick sort abbia una complessità nel caso peggiore di O(n²), la probabilità è davvero bassa. Quando si tratta dell'aumento di velocità, quick sort prevale su merge sort che è vincolato alla complessità O(n * log(n)), e quick sort finisce per avere delle prestazioni migliori in media.
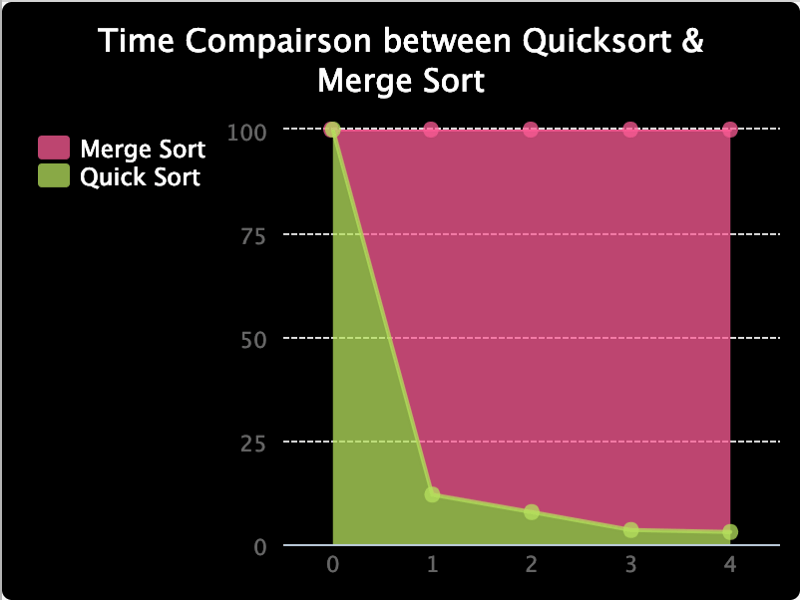
Ho anche realizzato il grafico qui sotto per confrontare il rapporto tra il tempo che impiegano, dato che è difficile vedere i loro valori. Come puoi vedere, il tempo percentuale impiegato per quick sort è in ordine discendente.
La morale della favola è che la notazione O grande è solo un'analisi matematica per fornire un riferimento alle risorse richieste da un algoritmo. Nella pratica, i risultati possono essere differenti, ma in generale, è una buona pratica tentare di abbattere la complessità di un algoritmo, finché non ci imbattiamo in un caso in cui sappiamo cosa stiamo facendo.
In conclusione…
Mi piace programmare, imparare cose nuove e condividerle con la comunità. Se c'è qualcosa che ti interessa particolarmente, per favore, fammelo sapere. Generalmente scrivo di web design, architettura del software, matematica e scienza dei dati. Puoi trovare alcuni articoli validi che ho scritto in precedenza se sei interessato a questi argomenti.
Buon divertimento con lo studio dell'informatica!!!


