L'algoritmo dei cammini minimi di Dijkstra - Una dettagliata introduzione grafica

Articolo originale: Dijkstra's Shortest Path Algorithm - A Detailed and Visual Introduction

Se hai sempre voluto conoscere e capire l'algoritmo di Dijkstra, questo è l'articolo che fa per te. Vedrai come funziona passo passo con delle spiegazioni grafiche.

In quest'articolo imparerai:

• Concetti di base dei grafi (un breve riassunto).
• Per cosa viene utilizzato l'algoritmo di Dijkstra.
• Come funziona in background con degli esempi.

Iniziamo! ✨

🔹 Introduzione ai grafi

Iniziamo con una breve introduzione sui grafi.

Concetti di base

I grafi sono strutture di dati usate per rappresentare "connessioni" tra coppie di elementi.

• Questi elementi vengono chiamati nodi e possono rappresentare oggetti della vita reale, persone o entità.
• Le connessioni tra i nodi sono chiamate archi.

Ecco una rappresentazione grafica di un grafo:

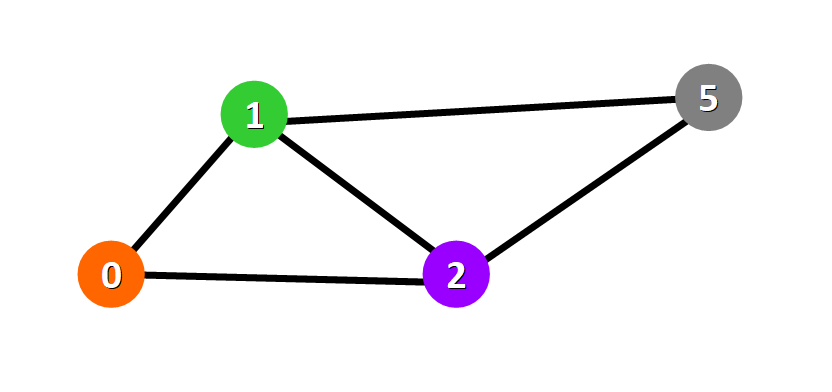
I nodi sono rappresentati con dei cerchi colorati e gli archi con delle linee che connettono i cerchi.

💡 Suggerimento: due nodi sono connessi se c'è un arco tra di loro.

Applicazioni

I grafi vengono utilizzati direttamente in situazioni reali. Ad esempio, possiamo usarli per progettare una rete di trasporto in cui i nodi rappresentano le strutture che inviano o ricevono dei prodotti e gli archi rappresentano le strade o i percorsi che le collegano (vedi qui sotto).

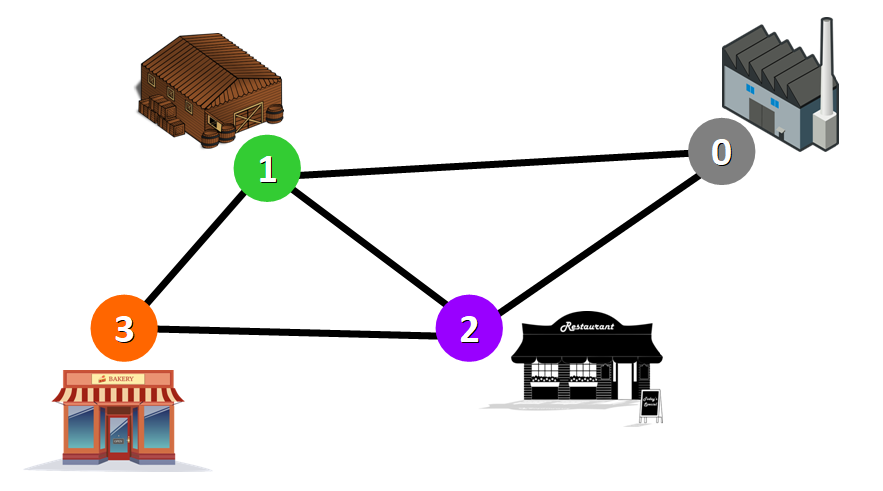
Tipi di grafi

I grafi possono essere:

• Non orientati: se per ogni coppia di nodi connessi, puoi andare da un nodo all'altro in entrambi i versi.
• Orientati: se per ogni coppia di nodi connessi, puoi muoverti da un nodo all'altro soltanto in una verso specifico. Utilizziamo delle frecce, invece di semplici linee, per rappresentare gli archi orientati.

💡 Suggerimento: in quest'articolo, avremo a che fare con grafi non orientati.

Grafi pesati

Un grafo pesato è un grafo ai cui archi è associato un "peso" o un "costo". Il peso di un arco può rappresentare una distanza, un tempo o qualsiasi altra cosa relativa alla connessione che l'arco stabilisce tra due nodi.

Ad esempio, nel grafo pesato qui sotto, puoi vedere un numero in blu, riportato vicino ad ogni arco. Questo numero viene usato per rappresentare il peso dell'arco corrispondente.

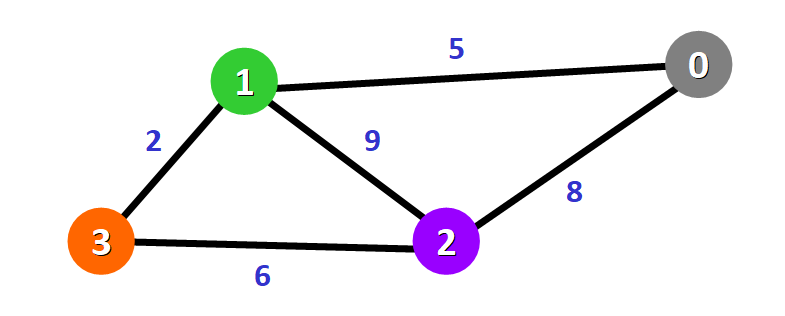
💡 Suggerimento: come vedrai tra poco, questi pesi sono essenziali per l'algoritmo di Dijkstra.

🔸 Introduzione all'algoritmo di Dijkstra

Adesso che conosci i concetti di base dei grafi, possiamo iniziare a parlare di questo meraviglioso algoritmo.

• Scopo e casi di utilizzo
• Storia
• Concetti di base dell'algoritmo di Dijkstra
• Requisiti

Scopo e casi di utilizzo

Con l'algoritmo di Dijkstra, puoi trovare il cammino minimo che intercorre tra i nodi di un grafo. In particolare, puoi trovare il cammino minimo tra un nodo (chiamato "nodo sorgente") e tutti gli altri nodi del grafo, producendo un albero dei cammini minimi.

Questo algoritmo viene usato nei dispositivi GPS per cercare il cammino minimo tra la località attuale e quella di destinazione e ha ampie applicazione nell'industria, specialmente in campi che richiedono la modellazione di network.

Storia

Questo algoritmo è stato creato e pubblicato da Dr. Edsger W. Dijkstra, un brillante informatico olandese e ingegnere del software.

Nel 1959, ha pubblicato un articolo di 3 pagine intitolato "A note on two problems in connexion with graphs" in cui ha illustrato il suo nuovo algoritmo.

Durante un'intervista nel 2001, il Dr. Dijkstra ha rivelato come e perché ha sviluppato l'algortitmo:

Come ottenere il percorso più breve per viaggiare da Rotterdam a Groningen? Con l'algoritmo per il cammino minimo che ho creato in circa 20 minuti. Una mattina, mi trovavo con la mia giovane fidanzata a fare shopping ad Amsterdam. Eravamo stanchi e ci siamo seduti sulla terrazza di un bar a bere un caffè, mentre stavo pensando a come risolvere questo problema e poi ho elaborato l'algoritmo per il cammino minimo. Come ho detto, è stata una invenzione da 20 minuti. Il lavoro fu pubblicato nel 1959, tre anni dopo. La pubblicazione è piuttosto bella e una  delle ragioni che la rende così bella è che ho progettato il tutto senza carta e penna. In questo modo, sei quasi forzato a evitare ogni inutile complessità. Alla fine quell'algoritmo è diventato, con mio grande stupore, una delle pietre angolari della mia fama. - Come citato nell'articolo Edsger W. Dijkstra da An interview with Edsger W. Dijkstra.

⭐ Incredibile, vero? In soli 20 minuti, il Dr. Dijkstra ha elaborato uno dei più famosi algoritmi nella storia dell'informatica.

Concetti di base dell'algoritmo di Dijkstra

• Sostanzialmente, l'algoritmo di Dijkstra parte dal nodo che scegli (il nodo sorgente) e analizza il grafo per trovare il percorso più breve tra quel nodo e tutti gli altri nodi del grafo.
• L'algoritmo tiene traccia delle attuali distanze più brevi tra ogni nodo e il nodo sorgente e aggiorna questi valori quando trova un percorso più breve.
• Una volta che l'algoritmo ha trovato il tragitto più breve tra il nodo sorgente e un altro nodo, quest'ultimo viene segnato come "visitato" a aggiunto al percorso.
• Il processo continua finché tutti i nodi nel grafo sono stati aggiunti al percorso. In questo modo, otteniamo un percorso che connette il nodo sorgente a tutti gli altri nodi seguendo il cammino più breve possibile per raggiungere ogni nodo.

Requisiti

L'algoritmo di Dijkstra funziona soltanto con grafi che hanno pesi positivi. Questo perché, durante il processo, i pesi degli archi vengono sommati per trovare il cammino minimo.

Se nel grafo è presente un peso negativo, l'algoritmo non funzionerà adeguatamente. Una volta che un nodo viene segnato come "visitato", il percorso attuale per quel nodo viene indicato come il più breve per raggiungerlo. Un peso negativo può alterare il processo se il peso totale viene ridotto dopo questo step.

🔹 Esempi dell'algoritmo di Dijkstra

Ora che ne sai di più su quest'algoritmo, vediamo come funziona dietro le quinte con un esempio passo passo.

Consideriamo il grafo:

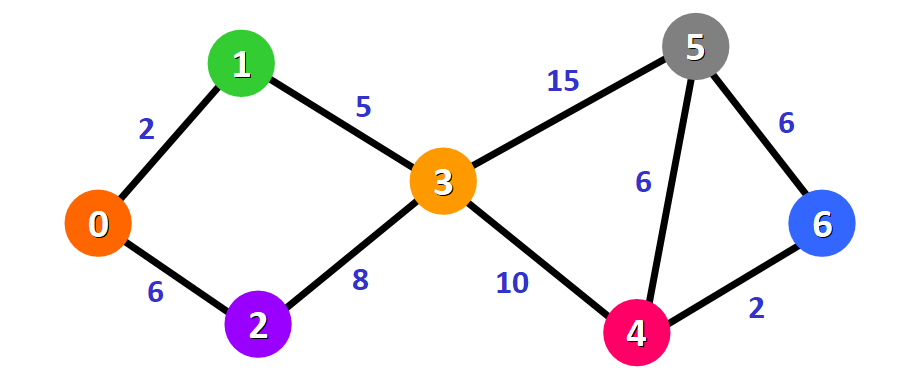
L'algoritmo genererà il percorso più breve tra il nodo 0 e tutti gli altri nodi nel grafo.

💡 Suggerimento: in questo grafo, assumeremo che i pesi degli archi rappresentino le distanze tra due nodi.

Il percorso più breve sarà quello tra il nodo 0 e il nodo 1, dal nodo 0 al nodo 2, dal nodo 0 al nodo 3 e così via per ogni nodo del grafo.

Inizialmente, abbiamo la lista delle distanze riportata di seguito:

• La distanza tra il nodo sorgente e sé stesso è 0. In quest'esempio, il nodo sorgente sarà il nodo 0 ma possiamo scegliere qualsiasi nodo.
• La distanza dal nodo sorgente a tutti gli altri nodi non è ancora stata determinata, quindi utilizziamo il simbolo di infinito per rappresentare questa condizione iniziale.

Abbiamo anche la seguente lista, che tiene traccia dei nodi che non sono stati ancora visitati (i nodi che non sono ancora stati inclusi nel percorso):

💡 Suggerimento: ricorda che l'algoritmo è completato una volta che tutti i nodi sono stati aggiunti al percorso.

Dato che abbiamo deciso di partire dal nodo 0, possiamo segnare questo nodo come visitato. In modo equivalente, lo cancelliamo dalla lista dei nodi non visitati e aggiungiamo un contorno rosso al nodo corrispondente nel diagramma:

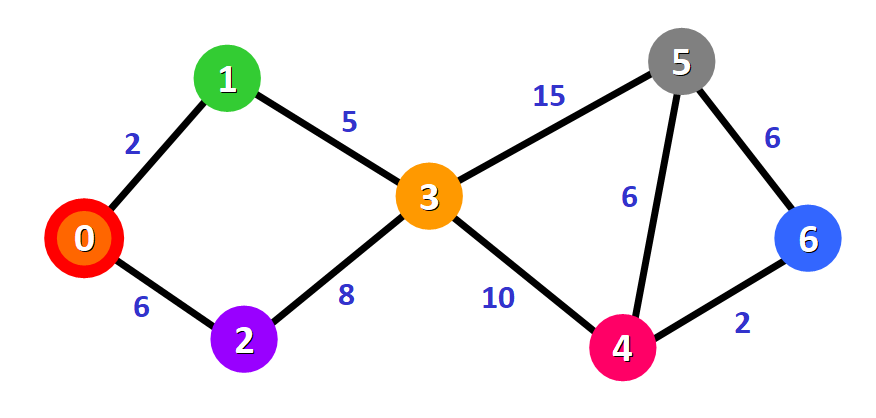
Adesso abbiamo bisogno di iniziare a verificare le distanze tra il nodo 0 e i nodi adiacenti. Come puoi vedere, si tratta dei nodi 1 e2 (vedi gli archi rossi):

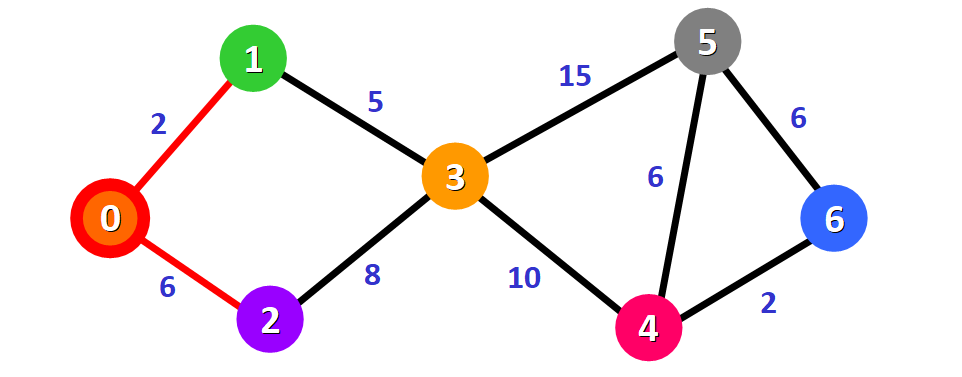
💡 Suggerimento: questo non significa che stiamo aggiungendo immediatamente i due nodi adiacenti al percorso più breve. Prima di fare ciò, dobbiamo verificare se abbiamo trovato il percorso più breve per raggiungerli. Stiamo semplicemente svolgendo una valutazione iniziale per analizzare le opzioni disponibili.

Dobbiamo aggiornare le distanze dal nodo 0 al nodo 1 e al nodo 2 con i pesi degli archi che li connettono al nodo 0 (il nodo sorgente). Questi pesi sono rispettivamente 2 e 6:

Una volta aggiornate le distanze dei nodi adiacenti, abbiamo bisogno di:

• Selezionare il nodo più vicino al nodo sorgente in base alle distanze attuali conosciute.
• Segnarlo come visitato.
• Aggiungerlo al percorso.

Se controlliamo la lista delle distanze, possiamo vedere che al nodo 1 corrisponde la distanza minore dal nodo sorgente (distanza di 2), quindi lo aggiungiamo al percorso.

Nel diagramma, lo rappresentiamo con un arco rosso:

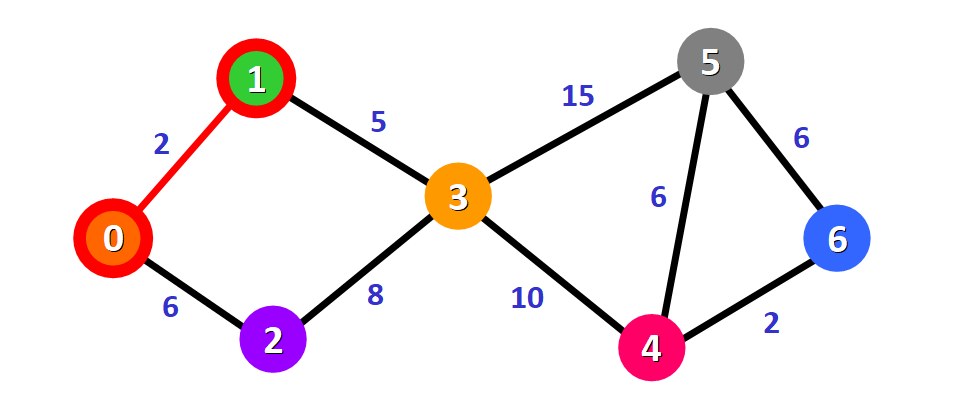
Lo segniamo con un quadrato rosso nella lista per indicare che è stato visitato e che abbiamo trovato il percorso più breve per questo nodo:

E lo cancelliamo dalla lista dei nodi non visitati:

Adesso dobbiamo analizzare i nuovi nodi adiacenti per trovare il percorso più breve per raggiungerli. Consideriamo soltanto i nodi adiacenti ai nodi che fanno già parte del percorso più breve (quello marcata dagli archi rossi).

I nodi 3 e 2 sono entrambi vicini ai nodi che fanno già parte del percorso perché, come puoi vedere qui sotto, sono direttamente collegati rispettivamente ai nodi 1 e 0. Questi sono i nodi che analizzeremo nel prossimo passaggio.

Dato che abbiamo già la distanza tra il nodo sorgente e il nodo 2 scritta nella nostra lista, stavolta non dobbiamo aggiornarla. Dobbiamo soltanto aggiornare la distanza tra il nodo sorgente e il nuovo nodo adiacente (nodo 3):

La distanza è 7. Vediamo perché.

Per trovare la distanza tra nodo sorgente e un altro nodo (in questo caso, il nodo 3), aggiungiamo i pesi di tutti gli archi che determinano il cammino minimo per raggiungere il nodo:

• Per il nodo 3: la distanza totale è 7 perché aggiungiamo i pesi degli archi che formano il percorso 0 -> 1 -> 3 (2  per l'arco 0 -> 1 e 5 per l'arco 1 -> 3).

Ora che conosciamo la distanza dei nodi adiacenti, dobbiamo scegliere quale nodo verrà aggiunto al percorso. Dobbiamo selezionare un nodo non visitato con la distanza minore (attualmente conosciuta) dal nodo sorgente.

Se diamo un'occhiata alla lista delle distanze, possiamo immediatamente renderci conto che è il nodo 2 alla distanza 6:

Lo aggiungiamo al percorso graficamente contrassegnandolo in rosso:

Segniamo il nodo come visitato aggiungendo un quadratino rosso nella lista delle distanze e cancellandolo dalla lista dei nodi non visitati:

Adesso abbiamo bisogno di ripetere il processo per trovare il percorso più breve dal nodo sorgente al nuovo nodo adiacente, ovvero il nodo 3.

Come puoi notare, ci sono due percorsi possibili: 0 -> 1 -> 3 o 0 -> 2 -> 3. Vediamo come stabilire quale dei due è il più corto.

La distanza del nodo 3 è già stata inserita nella lista (7, vedi la lista precedente). Questa distanza risultava da uno step precedente, in cui abbiamo aggiunto i pesi 5 e 2 degli archi da percorrere nel tragitto 0 -> 1 -> 3.

Adesso, abbiamo un'altra alternativa. Se scegliamo di seguire il percorso 0 -> 2 -> 3, avremo bisogno di passare per gli archi 0 -> 2 and 2 -> 3 che hanno rispettivamente peso 6 e 8, per una distanza totale di 14.

Chiaramente, la prima distanza è minore (7 vs 14), così sceglieremo il percorso originario 0 -> 1 -> 3. Aggiorniamo la distanza solo se il nuovo percorso è più corto.

Quindi, aggiungiamo questo nodo al percorso usando la prima alternativa: 0 -> 1 -> 3.

Segniamo il nodo come visitato e lo cancelliamo dalla lista dei nodi non visitati:

E ripetiamo di nuovo il processo.

Valutiamo i nodi adiacenti che non sono stati ancora visitati. Questa volta, si tratta dei nodi 4 e 5 dato che sono contigui al nodo 3.

Aggiorniamo le distanze di questi nodi dal nodo sorgente, cercando sempre il tragitto più corto:

• Per il nodo 4: la distanza è 17, seguendo il percorso  0 -> 1 -> 3 -> 4.
• Per il nodo 5: la distanza è 22 seguendo il percorso 0 -> 1 -> 3 -> 5.

💡 Suggerimento: nota che abbiamo considerato soltanto di estendere il percorso più breve (segnato in rosso). Non possiamo considerare di passare attraverso archi che non sono stati aggiunti al percorso più breve (ad esempio, non possiamo usare il percorso che contiene l'arco 2 -> 3).

Adesso, dobbiamo scegliere quale nodo non visitato verrà segnato come visitato. In questo caso, si tratta del nodo 4 perché ha la distanza minore nella lista delle distanze. Lo aggiungiamo graficamente al diagramma:

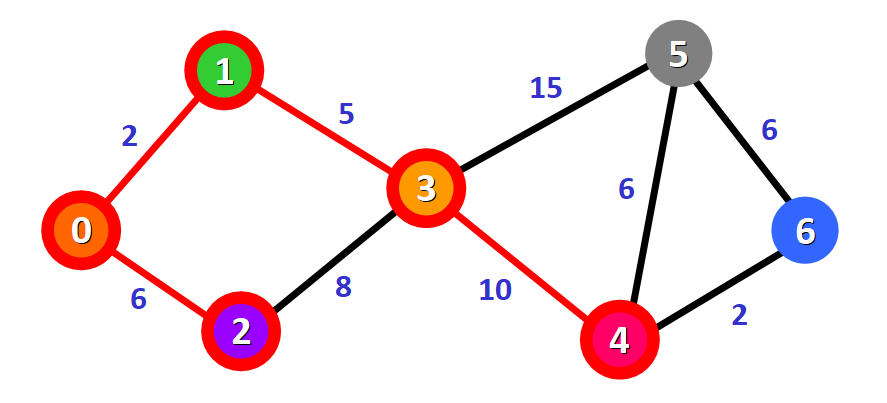
Inoltre, lo segniamo  come "visitato" aggiungendo un quadratino rosso nella lista:

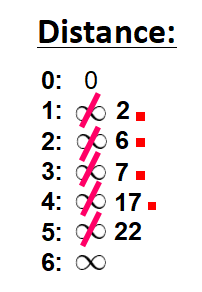
E lo cancelliamo dalla lista dei nodi non visitati:

Ripetiamo ancora il processo. Valutiamo i nodi adiacenti: nodi 5 e 6. Dobbiamo analizzare ogni possibile percorso che possiamo seguire per raggiungerli partendo dai nodi già visitati e aggiunti al percorso.

Per il nodo 5:

• La prima opzione è di seguire il percorso 0 -> 1 -> 3 -> 5, che ha distanza 22 dal nodo sorgente (2 + 5 + 15). Questa distanza è già stata registrata nella lista delle distanze nello step precedente.
• La seconda opzione è di seguire il percorso 0 -> 1 -> 3 -> 4 -> 5, che ha distanza 23 dal nodo sorgente (2 + 5 + 10 + 6).

Ovviamente, il primo percorso è più corto e lo scegliamo per raggiungere il nodo 5.

Per il nodo 6:

• Il percorso disponibile è 0 -> 1 -> 3 -> 4 -> 6, che ha distanza 19 dal nodo sorgente (2 + 5 + 10 + 2).

Segniamo come visitato il nodo con la distanza (attualmente conosciuta) più breve. In questo caso, il nodo 6.

E lo cancelliamo dalla lista dei nodi non visitati:

Adesso, abbiamo questo percorso (segnato in rosso):

Soltanto il nodo 5 non è stato ancora visitato. Vediamo come includerlo nel percorso.

Ci sono tre diversi percorsi che possiamo usare per raggiungere il nodo 5 dai nodi che abbiamo aggiunto al percorso:

• Opzione 1: 0 -> 1 -> 3 -> 5 con una distanza di 22 (2 + 5 + 15).
• Opzione 2: 0 -> 1 -> 3 -> 4 -> 5 con una distanza di 23 (2 + 5 + 10 + 6).
• Opzione 3: 0 -> 1 -> 3 -> 4 -> 6 -> 5 con una distanza di 25 (2 + 5 + 10 + 2 + 6).

Selezioniamo il percorso più breve: 0 -> 1 -> 3 -> 5 con una distanza di 22.

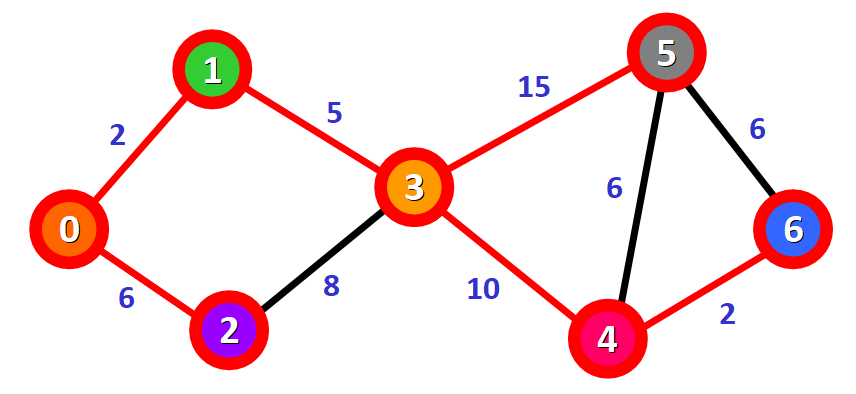
Segniamo il nodo come visitato e lo cancelliamo dalla lista dei nodi non visitati:

E voilà! Abbiamo il risultato finale del percorso più breve dal nodo 0 ad ogni nodo del grafo.

Nel diagramma, il percorso più breve è segnato in rosso. Devi seguire questi archi per percorrere il cammino minimo che collega un dato nodo con quello sorgente (nodo 0).

Ad esempio, se vuoi raggiungere il nodo 6 partendo dal nodo 0, devi semplicemente seguire gli archi evidenziati in rosso e percorrerai automaticamente 0 -> 1 -> 3 -> 4 - > 6.

🔸 In conclusione

• I grafi vengono utilizzati per creare modelli di connessioni tra oggetti, persone o entità. Sono costituiti da due elementi principali: nodi e archi. I nodi rappresentano gli oggetti e gli archi rappresentano le connessioni tra essi.
• L'algoritmo di Dijkstra trova il cammino minimo tra un dato nodo (denominato "sorgente") e tutti gli altri nodi in un grafo.
• Questo algoritmo utilizza i pesi degli archi per trovare il percorso che minimizza la distanza totale tra il nodo sorgente e gli altri nodi.

Spero davvero che quest'articolo ti sia piaciuto e che ti abbia aiutato. Adesso sai come funziona l'algoritmo di Dijkstra.