Artículo original escrito por Moshe Binieli
Artículo original Machine learning: an introduction to mean squared error and regression lines
Traducido y adaptado por andres-torres
Introducción
Este artículo tratará acerca del tema estadístico de error cuadrático medio y describirá la relación de este método con la regresión lineal, la regresión más básica en el contexto del aprendizaje automático (machine learning).
El ejemplo consiste de puntos en el eje cartesiano. Definiremos una función matemática que nos dará la línea recta que pasa en medio de todos los puntos del eje cartesiano.
De esta manera, aprenderemos la conexión entre estos dos métodos y cómo los resultados de su conexión aparecen juntos.
Explicación General
Contexto
El error cuadrático(MSE) mide el promedio de los errores elevados al cuadrado.
El hecho que el MSE es casi siempre estrictamente positivo(y no zero) es debido a la aleatoriedad o a que el estimador carece de información con la que pueda producir una mejor estimación.
La estructura del artículo
- Obtén una idea del ECM y su visualización gráfica.
- La parte matemática que contiene manipulaciones algebraicas y una derivación de una función de dos variables encontrando su mínimo.
- Esta sección es para quienes desean comprender el proceso de cómo obtenemos las fórmulas matemáticas finales. Puedes saltarte esta parte si tu interés no es este.
- Una explicación del rol de cada variable en la fórmula.
- Ejemplos.
Ideas Generales:
Supongamos que tenemos siete puntos, nuestro objetivo es encontrar la línea que minimiza la suma de las distancias elevadas al cuadrado de estos puntos.
Tratemos de comprender esto.
Tomemos un ejemplo y tracemos una línea en medio de siete puntos aleatorios.
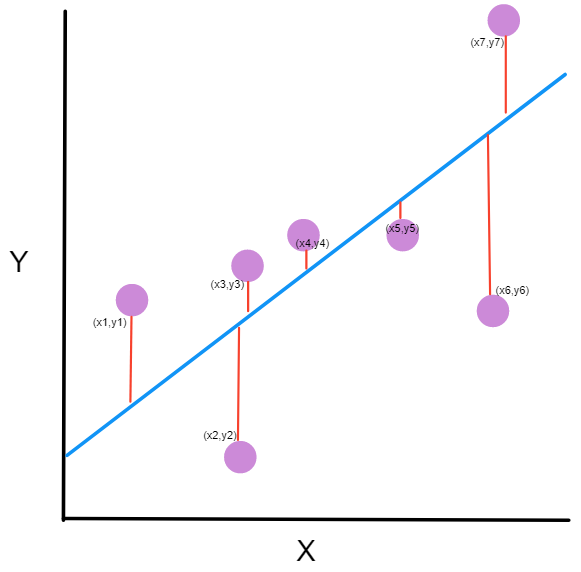
Podrías estar preguntándote ¿Qué significa esta gráfica?
- Los puntos púrpuras son los siete puntos aleatorios en la gráfica. Cada punto posee una coordenada X y una coordenada Y.
- La línea azul es nuestra línea de predicción. Es una línea que pasa a través de todos los puntos y que se ajusta a ellos de la mejor manera posible, de este modo esta línea contiene todos los puntos.
- La línea roja entre cada punto púrpura y la línea de predicción son los errores. Cada error es la distancia desde el punto hasta su punto estimado.
Puede que ahora recuerdes esta ecuación en tus días de escuela, y=Mx+B, donde M es la pendiente de la recta, y B es su intercepto.
Queremos encontrar la pendiente M y él interceptó B que minimiza el error cuadrático.
Definamos la ecuación matemática que nos proporcionará el error cuadrático medio para todos nuestros puntos.
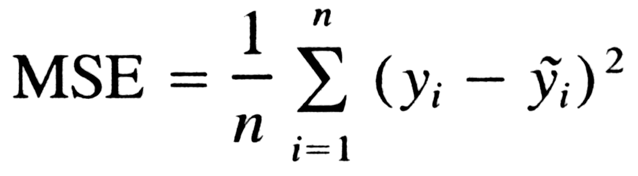
Analicemos el significado de esta ecuación.
- Sigma representa la suma de la secuencia de números desde i=1 hasta n. Imaginemos esto cómo un arreglo de puntos, donde en el proceso se pasa a través de todos los puntos, desde el primero (i=1) hasta el último (i=n).
- Por cada punto, tomamos la coordinada y del punto, y la coordenada y’. Sustraemos la coordenada y, de nuestra coordenada y’ (es decir los valores estimados) y calculamos el cuadrado del resultado.
- La tercera parte es tomar la suma de todos los valores (y-y’)², es decir, la diferencia entre los valores reales y estimados elevados al cuadrado.
- Finalmente procedemos a dividir esas diferencias al cuadrado por n y así obtenemos la media.
Nuestro objetivo es minimizar esta media. Lo que nos proveerá con la mejor línea que pasa a través de los puntos.
Del concepto a las ecuaciones matemáticas
Esta parte es para las personas que quieren comprender cómo obtenemos las ecuaciones matemáticas.
Cómo vimos anteriormente, tenemos la ecuación y=mx+b.
Tomemos cada punto en la gráfica, y luego haremos nuestro propio cálculo (y-y’)².
¿Pero cómo calculamos y? No tenemos qué porque es parte de los datos.
Recordemos la definición algebraica, de (y-y’)². A partir de aquí, obtenemos el desglose de la ecuación del error cuadrático medio (MSE):
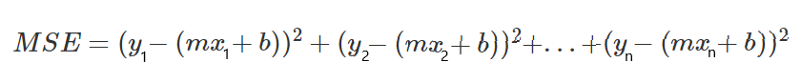
Reescribimos la ecuación y simplificamos.
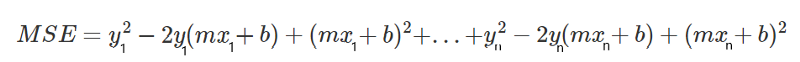
Comenzamos operando los paréntesis en la ecuación. Nótese la distinción anaranjada y morado de las ecuaciones.

Ahora, apliquemos otra manipulación. Juntaremos cada parte de la ecuación. Tomaremos todas la y, así como todas las (-2ymx) etc. En otras palabras, agrupación de términos.
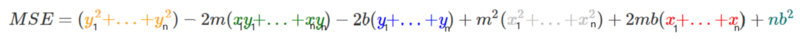
En este punto, podemos tomar la media de todos los valores elevados al cuadrado de y, xy, x, x².
Definamos para cada uno, un nuevo carácter que representará la media de todos los valores al cuadrado.
Veamos un ejemplo, tomemos todos los valores y, y luego dividamos por n (n representa el número de elementos), entonces obtendremos la media, y la llamaremos Y promedio.
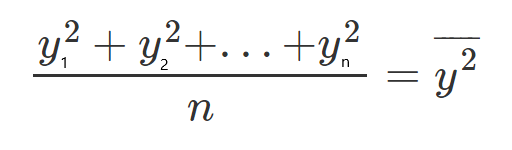
Si multiplicamos ambos lados de la ecuación por n, obtendremos:
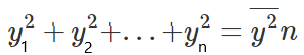
Esto nos llevará a la siguiente ecuación:

Tenemos una ecuación de tres dimensiones. Queremos encontrar los valores M y B(recordar la ecuación de la recta) que minimizan la función.
Debido a que es un problema de minimización, entramos al mundo del cálculo diferencial, la forma de minimizar una ecuación consiste en igualar a cero y luego derivar. Sin embargo, en este caso tenemos que tomar una derivada parcial. Tomamos la derivada parcial con respecto a M y la derivada parcial con respecto a B de nuestro MSE.
Ya que estamos buscando un punto mínimo, tomaremos las derivadas parciales, igualándolas a cero.
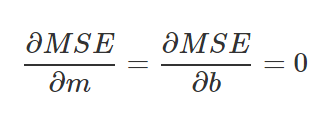
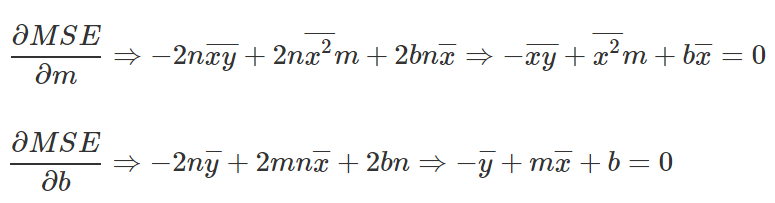
Tomemos las dos ecuaciones que acabamos de obtener, separando la variable b de ambas, y luego sustrayendo la primera ecuación de la segunda.
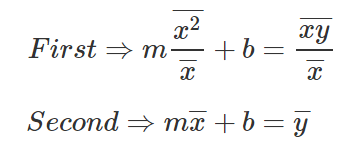
Pasamos a sustraer la primera ecuación de la segunda.
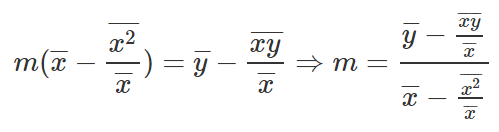
Nos deshacemos de los denominadores en la ecuación.
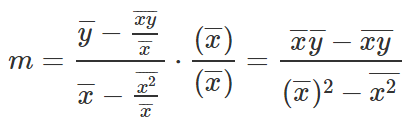
Y aquí estamos, esta es la ecuación para encontrar M, tomamos esta para escribir la ecuación B.
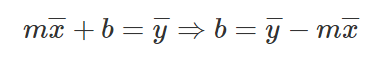
Ecuaciones para la pendiente y él interceptó y.
Estas serán las ecuaciones matemáticas que nos ayudarán a encontrar la pendiente y él interceptó.
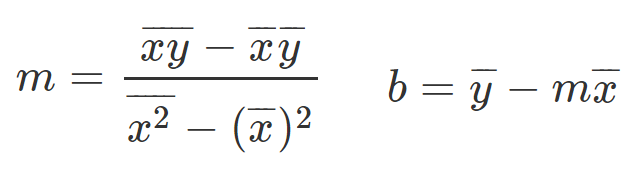
Hablemos un poco más acerca de estas ecuaciones:
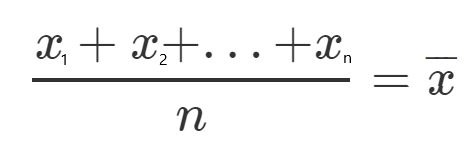
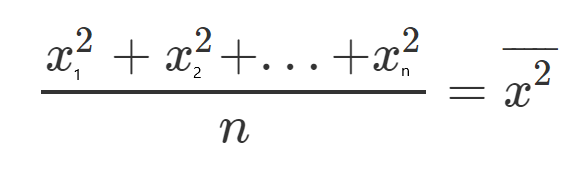
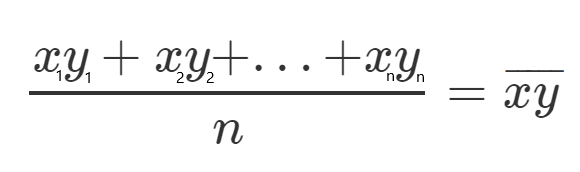
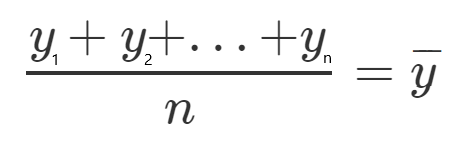
Ejemplos
Muchas Gracias a Khan Academy por los ejemplos.
Ejemplo #1
Tomemos 3 puntos, (1,2), (2,1), (4,3).

Encontremos M y B para la ecuación y=mx+b.
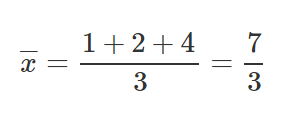
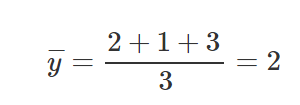
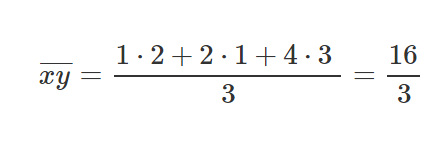
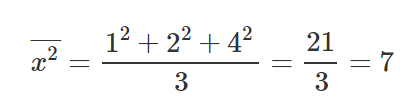
Luego de haber calculado las partes relevantes de nuestras ecuaciones pendientes e intercepto, sustituyamos algunos valores en las ecuaciones veamos cómo obtenemos una pendiente y un intercepto y.
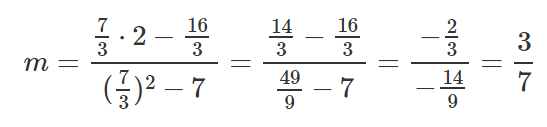

Tomemos estos resultados y definámoslos cómo una sola ecuación y=mx+b.

Ahora dibujemos la línea y veamos cómo esta pasa a través de los puntos a la vez que minimiza sus distancias elevadas al cuadrado.
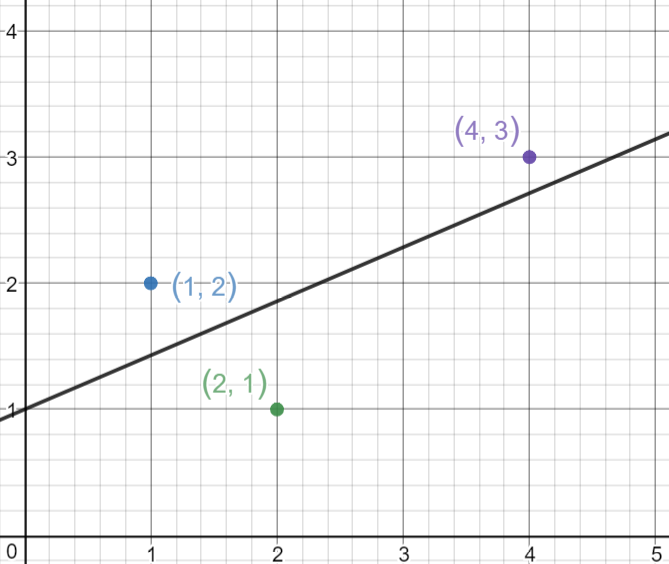
Ejemplo #2
Tomemos 4 puntos, (-2,-3), (-1,-1), (1,2), (4,3).

Vamos a encontrar M y B para la ecuación y = mx + b.
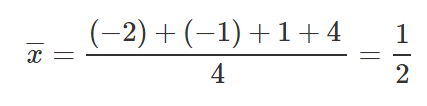


Lo mismo que antes, sustituyamos estos valores en las ecuaciones para encontrar M y B.
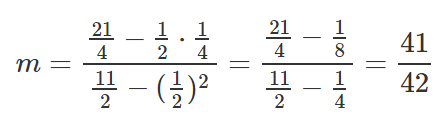

Definiendo estos resultados cómo una sola ecuación.
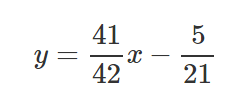
Ahora graficamos la línea y vemos cómo esta pasa a través de los puntos a la vez que minimiza sus distancias elevadas al cuadrado.
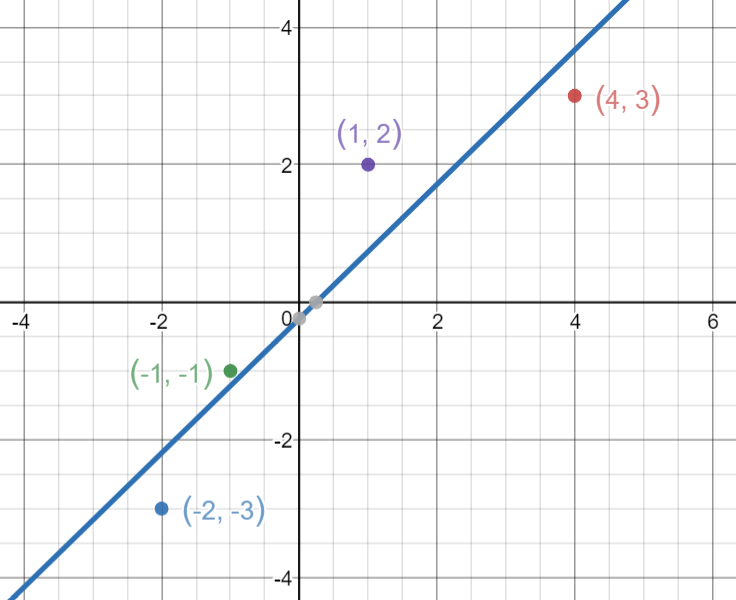
En Conclusión
Cómo puedes ver, la idea es simple. Solo es necesario comprender las partes principales y cómo trabajar con ellas.
Puedes trabajar con las fórmulas para encontrar la línea en otra gráfica, y así efectuar un cálculo simple, obteniendo los resultados para la pendiente y él interceptó.
Este artículo ha hecho más énfasis en el error cuadrático medio y los aspectos matemáticos de la línea de regresión que minimiza el MSE. No tanto así en el aspecto intuitivo y de aplicación práctica que se encuentran fuera del alcance del artículo.
No obstante, la regresión lineal suele ser de las primeras lecciones en aprendizaje automático e inteligencia artificial, por lo tanto es muy importante conocer su aspecto matemático.
Muchas Gracias por tu atención.

