by Kevin Turney
Voy a decir esto desde el principio. ¿Sabes que es lo que ocurre cuando una función es invocada? ¿No? Entonces ahí es donde empezaremos.
Invocación de función
Cuando llamamos a una función, un contexto de ejecución se coloca en la pila de ejecución. Analicemos esto un poco mas.
Primero, ¿Qué es una pila?
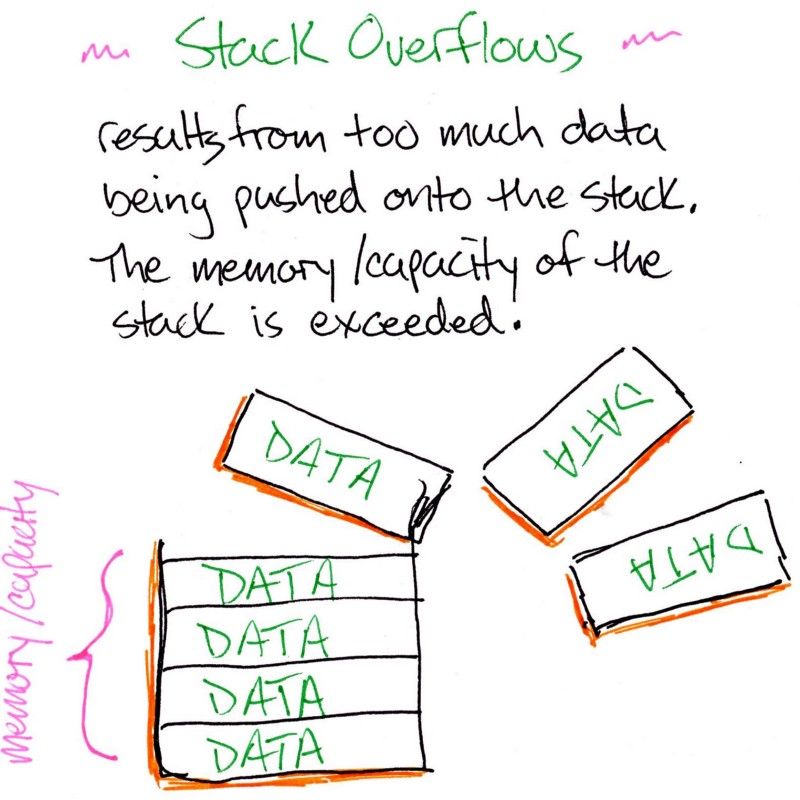
Una pila (stack) es una estructura de datos que opera sobre la base de "último en entrar, primero en salir". Un elemento es “apilado” (push) sobre una pila para añadirlo a esta, y un elemento es “retirado” (pop) de la pila para quitarlo.
Usar una pila es un método para ordenar ciertas operaciones para su ejecución.
Ahora, de regreso a ¿Qué es un contexto de ejecución? Un contexto de ejecución se forma una vez que una función se invoque. Este contexto se coloca a si mismo en una pila de ejecución, un orden de operaciones. El elemento que siempre esta primero en esta pila es el contexto de ejecución global. Seguido de este están los contextos creados por una función.
Estos contextos de ejecución tienen propiedades, un Objecto de Activación y un enlace “this”. El enlace “this” es una referencia a este contexto de ejecución. El objeto de activación incluye: parámetros pasados, variables declaradas, y declaraciones de funciones.
Así que cada vez que colocamos un nuevo contexto en la pila, usualmente tenemos todo lo que necesitamos para ejecutar código.
¿Por qué digo usualmente?
Con recursión, nosotros estamos esperando valores de retorno que vienen de otros contextos de ejecución. Estos otros contextos están mas arriba en la pila. Cuando el ultimo elemento en la pila termina la ejecución, ese contexto genera un valor de retorno. Este valor de retorno se pasa como un valor devuelto del caso recursivo al siguiente elemento. Ese contexto de ejecución luego es sacado de la pila.
Recursión
Entonces, ¿Qué es recursión?
Una función recursiva es una función que se llama a si misma hasta que una “condición base” sea verdad, y la ejecución se detiene.
Mientras sea falso, seguiremos colocando contextos de ejecución encima de la pila. Esto puede suceder hasta que tengamos un “desbordamiento de pila”. Un desbordamiento de pila es cuando nos quedamos sin memoria para guardar elementos en la pila.

En general, una función recursiva tiene al menos dos partes: una condición base y al menos un caso recursivo.
Veamos un ejemplo clásico.
Factorial
const factorial = function(num) { debugger; if (num === 0 || num === 1) { return 1 } else { return num * factorial(num - 1) }}factorial(5)Aquí estamos tratando de encontrar 5! (cinco factorial). La función factorial se define como el producto de todos los enteros positivos menos que o igual a sus argumentos.
La primera condición dice: “si el parámetro pasado es igual a 0 o 1, vamos a salir y regresar 1”.
Siguiente, el caso recursivo establece:
“Si el parámetro no es 0 o 1, entonces pasaremos el valor de num multiplicado por el valor de retorno de llamar esta función otra vez con num-1 como su argumento”.
Entonces si llamamos factorial(0), la función regresa 1 y nunca toca el caso recursivo.
Lo mismo aplica para factorial(1).
Podemos ver lo que esta pasando si insertamos un enunciado de depuración en el código y usamos las herramientas de desarrollador para pasar a través de él y mirar la pila de llamadas.
- La pila de ejecución coloca
factorial()con 5 como argumento pasado. El caso base es falso, entra en la condición recursiva. - La pila de ejecución coloca
factorial()por segunda vez connum-1= 4 como argumento. El caso base es falso, entra en la condición recursiva. - La pila de ejecución coloca
factorial()por tercera ocasión connum-1(4–1) = 3 como argumento. El caso base es falso, entra en la condición recursiva. - La pila de ejecución coloca
factorial()por cuarta ocasión connum-1(3–1) = 2 como argumento. El caso base es falso, entra en la condición recursiva. - La pila de ejecución coloca
factorial()por quinta ocasión connum-1(2–1) = 1 como argumento. Ahora el caso base es verdad, entonces regresa 1.
En este punto, hemos disminuido el argumento por uno en cada llamada de función hasta que alcancemos una condición para devolver 1.
6. A partir de aquí se completa el último contexto de ejecución, num === 1, entonces esa función regresa 1.
7. Siguiente num === 2, entonces el valor de retorno es 2. (1×2).
8. Siguiente num === 3, entonces el valor de retorno es 6, (2×3).
Hasta ahora tenemos 1×2×3.
9. Siguiente, num === 4, (4×6). 24 es el valor de retorno al siguiente contexto.
10. Finalmente, num === 5, (5×24)y tenemos 120 como el valor final.

La recursividad es bastante genial, ¿verdad?
Pudimos haber hecho lo mismo con un ciclo for o while. Pero el uso de la recursividad produce una solución elegante que es más legible.
Por eso utilizamos soluciones recursivas.
Muchas veces, un problema roto en partes mas pequeñas es mas eficiente. Dividir un problema en partes más pequeñas ayuda a superarlo. Por lo tanto, la recursividad es un enfoque de divide y vencerás para resolver problemas
- Sub-problemas son mas fáciles de resolver que el problema original.
- Soluciones a sub-problemas son combinadas para resolver el problema original.
“Divide y vencerás” se utiliza con mayor frecuencia para recorrer o buscar estructuras de datos como árboles de búsqueda binaria, gráficos, y montículos. También funciona para muchos algoritmos de clasificación, como ordenamiento rápido y ordenamiento por montículos.
Trabajemos con los siguientes ejemplos.Usa las herramientas de desarrollador para tener una idea conceptual de lo que está sucediendo, dónde y cuándo. Recuerda usar enunciados de depuración y paso por cada proceso.
Fibonacci
const fibonacci = function(num) { if (num <= 1) { return num } else { return fibonacci(num - 1) + fibonacci(num - 2) }}fibonacci(5);Arreglos recursivos
function flatten(arr) { var result = [] arr.forEach(function(element) { if (!Array.isArray(element)) { result.push(element) } else { result = result.concat(flatten(element)) } }) return result}flatten([1, [2], [3, [[4]]]]);Invertir una cadena
function reverse(str) { if (str.length === 0) return '' return str[str.length - 1] + reverse(str.substr(0, str.length - 1))}reverse('abcdefg');Ordenamiento rápido
function quickSort(arr, lo, hi) { if (lo === undefined) lo = 0 if (hi === undefined) hi = arr.length - 1 if (lo < hi) { // partition the array var p = partition(arr, lo, hi) console.log('partition from, ' + lo + ' to ' + hi + '=> partition: ' + p) // sort subarrays quickSort(arr, lo, p - 1) quickSort(arr, p + 1, hi) } // for initial call, return a sorted array if (hi - lo === arr.length - 1) return arr}function partition(arr, lo, hi) { // choose last element as pivot var pivot = arr[hi] // keep track of index to put pivot at var pivotLocation = lo // loop through subarray and if element <= pivot, place element before pivot for (var i = lo; i < hi; i++) { if (arr[i] <= pivot) { swap(arr, pivotLocation, i) pivotLocation++ } } swap(arr, pivotLocation, hi) return pivotLocation}function swap(arr, index1, index2) { if (index1 === index2) return var temp = arr[index1] arr[index1] = arr[index2] arr[index2] = temp console.log('swapped' + arr[index1], arr[index2], +' in ', arr) return arr}quickSort([1, 4, 3, 56, 9, 8, 7, 5])Practicar técnicas de recursividad es importante. Para estructuras de datos anidadas como arboles, gráficos, y montículos, la recursividad es invaluable.
En un artículo futuro, Analizaré las técnicas de memorización y optimización de llamadas de cola en lo que respecta a la recursividad. ¡Gracias por leer!
Traducido del artículo de Kevin Turney - Recursion is not hard: a step-by-step walkthrough of this useful programming technique