by Kevin Turney
Recursion is not hard: a step-by-step walkthrough of this useful programming technique

I’m going to say this right off the bat. Do you know the events that happen upon function invocation? No? Then that’s where we will start.
Function invocation
When we call a function, an execution context gets placed on the execution stack. Let’s break this down some more.
First, what is a stack?
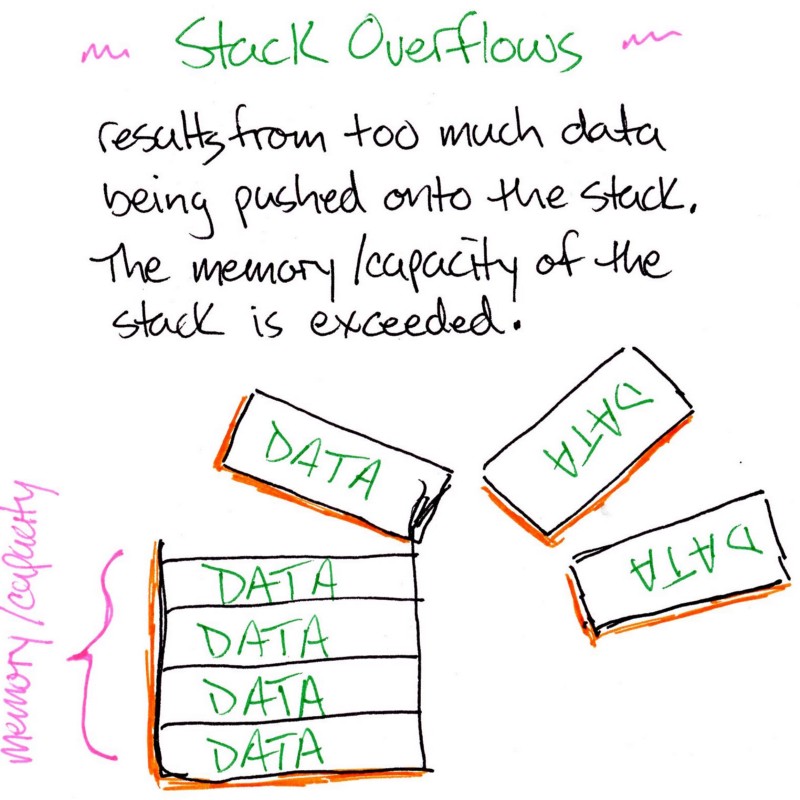
A stack is a data structure that operates on a “Last In, First Out” basis. An item is “pushed” onto a stack to add to it, and an item is “popped” off the stack to remove it.
Using a stack is a method of ordering certain operations for execution.
Now, back to what is an execution context? An execution context forms upon a function invocation. This context places itself on an execution stack, an order of operations. The item that is always first in this stack is the global execution context. Next up are any function created contexts.
These execution contexts have properties, an Activation Object and a “this” binding. The “this” binding is a reference back to this execution context. The Activation Object includes: parameters passed, declared variables, and function declarations.
So every time we place a new context on the stack, we usually have everything we need to execute code.
Why do I say usually?
With recursion, we are waiting for return values coming from other execution contexts. These other contexts are higher up the stack. When the last item on the stack finishes execution, that context generates a return value. This return value gets passed down as a return value from the recursive case to the next item. That execution context is then popped off the stack.
Recursion
So, what is recursion?
A recursive function is a function that calls itself until a “base condition” is true, and execution stops.
While false, we will keep placing execution contexts on top of the stack. This may happen until we have a “stack overflow”. A stack overflow is when we run out of memory to hold items in the stack.

In general, a recursive function has at least two parts: a base condition and at least one recursive case.
Let’s look at a classic example.
Factorial
const factorial = function(num) { debugger; if (num === 0 || num === 1) { return 1 } else { return num * factorial(num - 1) }}factorial(5)Here we are trying to find 5! (five factorial). The factorial function is defined as the product of all positive integers less than or equal to its argument.
The first condition states: “if the parameter passed equals 0 or 1, we will exit and return 1”.
Next, the recursive case states:
“If the parameter is not 0 or 1, then we will pass value of num times the return value of calling this function again with num-1 as its argument”.
So if we call factorial(0), the function returns 1 and never hits the recursive case.
The same holds for factorial(1).
We can see what is happening if we insert a debugger statement into the code and use devtools to step though it and watch the call stack.
- The execution stack places
factorial()with 5 as the argument passed. The base case is false, so enter the recursive condition. - The execution stack places
factorial()a second time withnum-1= 4 as argument. Base case is false, enter recursive condition. - The execution stack places
factorial()a third time withnum-1(4–1) = 3 as argument. Base case is false, enter recursive condition. - The execution stack places
factorial()a fourth time withnum-1(3–1) = 2 as argument. Base case is false, enter recursive condition. - The execution stack places
factorial()a fifth time withnum-1(2–1) = 1 as argument. Now the base case is true, so return 1.
At this point, we have decreased the argument by one on each function call until we reach a condition to return 1.
6. From here the last execution context completes, num === 1, so that function returns 1.
7. Next num === 2, so the return value is 2. (1×2).
8. Next num === 3, sothe return value is 6, (2×3).
So far we have 1×2×3.
9. Next, num === 4, (4×6). 24 is the return value to the next context.
10. Finally, num === 5, (5×24) and we have 120 as the final value.

Recursion is pretty neat, right?
We could have done the same thing with a for or a while loop. But using recursion yields an elegant solution that is more readable.
This is why we use recursive solutions.
Many times, a problem broken down into smaller parts is more efficient. Dividing a problem into smaller parts aids in conquering it. Hence, recursion is a divide-and-conquer approach to solving problems.
- Sub-problems are easier to solve than the original problem
- Solutions to sub-problems are combined to solve the original problem
“Divide-and-conquer” is most often used to traverse or search data structures such as binary search trees, graphs, and heaps. It also works for many sorting algorithms, like quicksort and heapsort.
Let’s work through the following examples. Use devtools to get a conceptual grasp of what’s happening where and when. Remember to use debugger statements and step though each process.
Fibonacci
const fibonacci = function(num) { if (num <= 1) { return num } else { return fibonacci(num - 1) + fibonacci(num - 2) }}fibonacci(5);Recursive arrays
function flatten(arr) { var result = [] arr.forEach(function(element) { if (!Array.isArray(element)) { result.push(element) } else { result = result.concat(flatten(element)) } }) return result}flatten([1, [2], [3, [[4]]]]);Reversing a string
function reverse(str) { if (str.length === 0) return '' return str[str.length - 1] + reverse(str.substr(0, str.length - 1))}reverse('abcdefg');Quicksort
function quickSort(arr, lo, hi) { if (lo === undefined) lo = 0 if (hi === undefined) hi = arr.length - 1 if (lo < hi) { // partition the array var p = partition(arr, lo, hi) console.log('partition from, ' + lo + ' to ' + hi + '=> partition: ' + p) // sort subarrays quickSort(arr, lo, p - 1) quickSort(arr, p + 1, hi) } // for initial call, return a sorted array if (hi - lo === arr.length - 1) return arr}function partition(arr, lo, hi) { // choose last element as pivot var pivot = arr[hi] // keep track of index to put pivot at var pivotLocation = lo // loop through subarray and if element <= pivot, place element before pivot for (var i = lo; i < hi; i++) { if (arr[i] <= pivot) { swap(arr, pivotLocation, i) pivotLocation++ } } swap(arr, pivotLocation, hi) return pivotLocation}function swap(arr, index1, index2) { if (index1 === index2) return var temp = arr[index1] arr[index1] = arr[index2] arr[index2] = temp console.log('swapped' + arr[index1], arr[index2], +' in ', arr) return arr}quickSort([1, 4, 3, 56, 9, 8, 7, 5])Practicing recursive techniques is important. For nested data structures like trees, graphs, and heaps, recursion is invaluable.
In a future article, I will discuss tail-call optimization and memoization techniques as they relate to recursion. Thanks for reading!