A regra de Simpson: a fórmula e como ela funciona

Artigo original: Simpson's Rule: the Formula and How it Works

A regra de Simpson é um método para a integração numérica. Em outras palavras, ela é a aproximação numérica de integrais definidas.

A regra de Simpson é a seguinte:

Nela,

• f(x) é chamado de integrando
• a = limite inferior da integração
• b = limite superior da integração

Regra 1/3 de Simpson

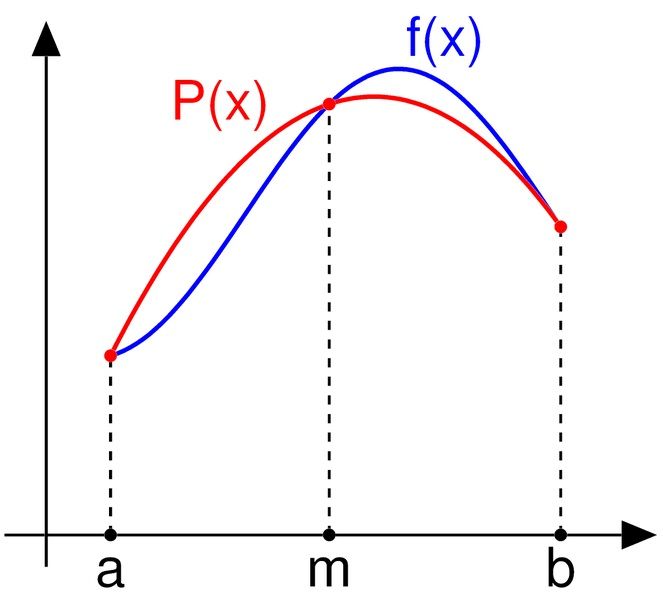
Como mostra o gráfico acima, o integrando f(x) é aproximado por um polinômio de segunda ordem; o interpolador quadrático é P(x).

Temos a aproximação conforme segue:

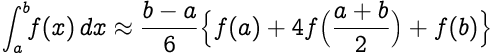
Substituindo (b-a)/2 por h, temos:

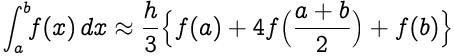
Como se pode ver, existe um fator de 1/3 na expressão acima. É por isso que ela é chamada de Regra 1/3 de Simpson.

Se uma função oscilar excessivamente e não tiver derivadas em determinados pontos, a regra acima pode não produzir resultados precisos.

Uma maneira comum de se lidar com isso é usar a abordagem composta da regra de Simpson. Para fazer isso, divida [a,b] em subintervalos menores, aplicando a regra de Simpson a cada subintervalo. Em seguida, some os resultados de cada cálculo para produzir uma aproximação da integral inteira.

Se o intervalo [a,b] for dividido em n subintervalos, e se n for um número par, a regra composta de Simpson é calculada com a seguinte fórmula:

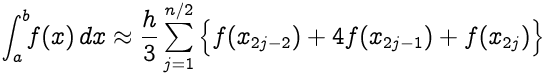
onde x_j = a+jh para j = 0,1,…,n-1,n com h=(b-a)/n; especificamente, x₀ = a e x_n = b.

Exemplo em C++:

Para aproximar o valor da integral fornecida abaixo, onde n = 8:

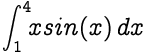
#include<iostream>
#include<cmath>
using namespace std;

float f(float x)
{
	return x*sin(x);	//Defina a função f(x)
}

float simpson(float a, float b, int n)
{
	float h, x[n+1], sum = 0;
	int j;
	h = (b-a)/n;
	
	x[0] = a;
	
	for(j=1; j<=n; j++)
	{
		x[j] = a + h*j;
	}
	
	for(j=1; j<=n/2; j++)
	{
		sum += f(x[2*j - 2]) + 4*f(x[2*j - 1]) + f(x[2*j]);
	}
	
	return sum*h/3;
}

int main()
{
	float a,b,n;
	a = 1;		//Insira o limite inferior a
	b = 4;		//Insira o limite superior b
	n = 8;		//Insira o comprimento do passo n
	if (n%2 == 0)
		cout<<simpson(a,b,n)<<endl;
	else
		cout<<"n deve ser um número par";
	return 0;
}

Regra 3/8 de Simpson

A regra 3/8 de Simpson é semelhante à regra 1/3 de Simpson. A única diferença está no fato de que, para a regra 3/8, o interpolador é um polinômio cúbico. Embora a regra 3/8 use mais um valor de função, ela é duas vezes mais precisa que a regra 1/3.

A regra 3/8 de Simpson determina que:

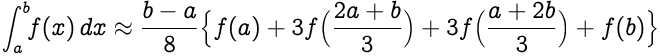
Substituindo (b-a)/3 por h, temos:

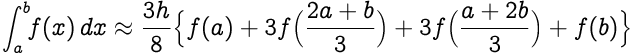
A regra 3/8 de Simpson para n intervalos (onde n deve ser um múltiplo de 3):

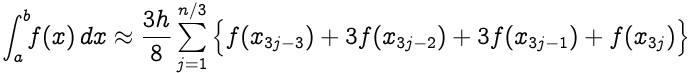
onde x_j = a+jh para j = 0,1,…,n-1,n com h=(b-a)/n; especificamente, x₀ = a e x_n = b.