Artigo original: https://www.freecodecamp.org/news/big-o-notation-why-it-matters-and-why-it-doesnt-1674cfa8a23c/
Você entende de fato a notação Big O? Se entende, este artigo ajudará a refrescar a memória antes de uma entrevista. Caso contrário, não se preocupe — venha e junte-se a nós nessa viagem pela Ciência da Computação.
Se você já fez cursos relacionados com algoritmos, já ouviu falar do termo notação Big O. Se ainda não fez, vamos examinar essa notação aqui e buscar um entendimento maior sobre o que ela é de fato.
A notação Big O é uma das ferramentas mais importantes para os cientistas da computação analisarem o custo de um algoritmo. É uma prática recomendada para engenheiros de software entendê-la bem.
Este artigo foi escrito tendo em conta que você já mexeu com código em algum momento. Além disso, algumas partes mais "profundas" do material também requerem um conhecimento de matemática do ensino médio. Assim, pode ser um pouco menos confortável para iniciantes. Se, no entanto, você sentir que está pronto, vamos começar!
Neste artigo, discutiremos em profundidade a notação Big O. Começaremos com um algoritmo de exemplo para ampliar sua compreensão. Depois, veremos um pouco de matemática para termos um entendimento mais formal. Depois disso, veremos algumas variações comuns da notação Big O. No fim, veremos algumas das limitações da Big O em um cenário prático. Confira o sumário abaixo.
Sumário
- O que é a notação Big O e qual a sua importância
- Definição formal da notação Big O
- Big O, Little O, Omega e Theta
- Comparação de complexidade entre as Big Os típicas
- Complexidade de tempo e de espaço
- Complexidade ideal, média, de pior caso e esperada
- Por que a Big O não importa
- No fim das contas…
Vamos começar.
1. O que é a notação Big O e qual a sua importância
"A notação Big O é uma notação matemática que descreve o comportamento limitante de uma função quando o argumento tende a um valor específico ou ao infinito. Ela pertence a uma família de notações inventadas por Paul Bachmann, Edmund Landau e outros, coletivamente chamadas de notação Bachmann–Landau ou de notação assintótica."
— Definição da Wikipédia de notação Big O
Dito de modo um pouco mais simples, a notação Big O descreve a complexidade do seu código usando termos algébricos.
Para entender o que é a notação Big O, vamos dar uma olhada em um exemplo típico, O(n²), que geralmente é chamada também de "Big O quadrática". A letra "n" representa o tamanho da entrada, enquanto a função "g(n) = n²" interna ao "O()" nos dá a ideia da complexidade do algoritmo em relação ao tamanho da entrada.
Um algoritmo típico que tem a complexidade O(n²) seria o algoritmo selection sort (algoritmo de ordenação por seleção). O selection sort é um algoritmo de ordenação que itera por uma lista para garantir que cada elemento em um índice i seja o i-ésimo elemento menor/maior da lista. Abaixo, vemos um CODEPEN que nos dá um exemplo visual disso.
O algoritmo pode ser descrito pelo código abaixo. Para garantir que o i-ésimo elemento seja o i-ésimo menor elemento da lista, este algoritmo itera primeiramente por toda a lista por meio de um laço for. Depois, para cada elemento, ele usa outro laço for para encontrar o menor elemento na parte restante da lista.
SelectionSort(Lista) {
for(i de 0 a Lista.Length) {
MenorElemento = Lista[i]
for(j de i a Lista.Length) {
if(MenorElemento > Lista[j]) {
MenorElemento = Lista[j]
}
}
Inverte(Lista[i], MenorElemento)
}
}Neste cenário, vamos considerar a variável Lista como a entrada. Desse modo, o tamanho da entrada n é o número de elementos dentro da Lista. Levamos em conta que a instrução if e que a atribuição de valor ligada à instrução if levam um tempo constante. Assim, descobriremos a notação big O da função SelectionSort analisando quantas vezes as instruções serão executadas.
Primeiro, o laço interno executa as instruções dentro dele n vezes. Depois, após incrementar o i, o laço for interno é executado n-1 vezes… até executar uma última vez, quando os dois laços for chegarão à sua condição de encerramento.
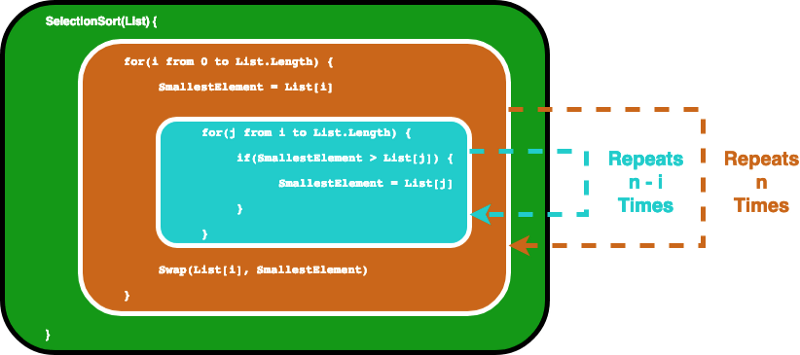
Isso acaba nos dando uma soma geométrica. A matemática do ensino médio nos ajudará a perceber que o laço interno se repetirá 1+2 … + n vezes, o que é igual a n(n-1)/2 vezes. Se multiplicarmos isso, teremos n²/2-n/2.
Ao calcularmos a notação big O, nos importamos apenas com os dermos dominantes, sem nos importarmos com os coeficientes. Assim, assumimos que n² é a nossa big O final. Escrevemos isso como O(n²), o que, novamente, é chamado de "Big O quadrática".
Você pode estar se perguntando o que é um "termo dominante". E, talvez, o motivo de não nos importarmos com os coeficientes. Mas não se preocupe, veremos os motivos um por um. Pode ser um pouco difícil de entender no início, mas tudo fará mais sentido depois de você ler a próxima seção.
2. Definição formal da notação Big O
Era uma vez um rei indiano que queria recompensar um homem sábio por seu excelente trabalho. O homem sábio pediu a ele apenas trigo suficiente para preencher um tabuleiro de xadrez.
A única regra era: na primeira casa, ele queria 1 grão de trigo, depois 2 na segunda, 4 na terceira… cada casa no tabuleiro de xadrez precisava ser preenchido com o dobro da quantidade de grãos da casa anterior. O rei inocente concordou sem hesitar, pensando que seria uma demanda simples de atender, até que finalmente tentou fazê-lo…

Quantos grãos de trigo o rei acabou devendo ao homem sábio? Sabemos que um tabuleiro de xadrez tem 8 por 8 casas, totalizando 64. Assim, a última casa terá 2⁶⁴ grãos de trigo. Se fizer os cálculos on-line, chegará a 1,8446744*10¹⁹, ou cerca de 18 seguido de 18 zeros. Levando em conta que cada grão pesa 0,01 gramas, isso nos dá 184.467.440.737 toneladas de trigo. E 184 bilhões de toneladas é bastante, não?
Os números crescem muito rapidamente com o crescimento exponencial, não é mesmo? A lógica também serve para algoritmos computacionais. Se o esforço exigido para realizar uma tarefa cresce exponencialmente com relação ao tamanho da entrada, ele pode acabar sendo incrivelmente grande.
Bem, o quadrado de 64 é 4096. Se você adicionar 4096 ao número 2⁶⁴, será um valor desprezível com relação aos algarismos significativos. É por isso que, ao olharmos para a taxa de crescimento, só nos importamos com os termos dominantes. Como queremos analisar o crescimento com relação ao tamanho da entrada, os coeficientes que apenas multiplicam o valor em vez de crescer juntamente com o tamanho da entrada não contêm informações úteis.
Abaixo, vemos a definição formal de Big O (em inglês):
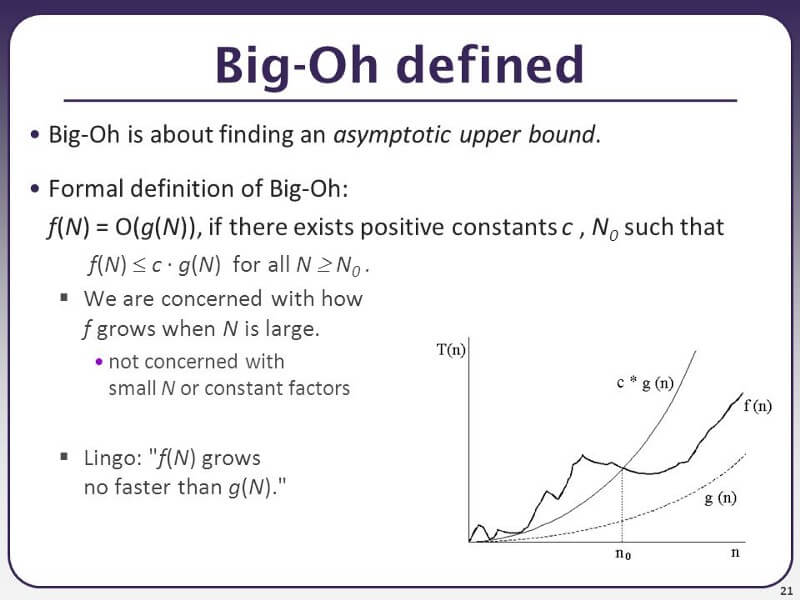
A definição formal é útil quando precisamos realizar uma prova matemática. Por exemplo, a complexidade de tempo para a ordenação por seleção pode ser definida pela função f(n) = n²/2-n/2, como mostramos na seção anterior.
Se nossa função g(n) for representada por n², encontramos uma constante c = 1 e um N₀ = 0. Enquanto N > N₀, N² será sempre maior que N²/2-N/2. Podemos provar isso facilmente subtraindo N²/2 de ambas as funções, quando veremos facilmente que N²/2 > -N/2 é verdadeiro quando N > 0. Portanto, podemos chegar à conclusão que f(n) = O(n²), na outra selection sort, é uma "big O quadrática".
Você pode ter percebido um truque aqui. Se você fizer g(n) crescer muito rápido, O(g(n)) sempre será suficientemente grande. Por exemplo, para qualquer função polinomial, você pode ter certeza ao dizer que são O(2ⁿ), pois 2ⁿ em algum momento ultrapassará qualquer polinômio.
Matematicamente, você está certo, mas quando falamos sobre Big O em geral, queremos saber o limite estrito da função. Você entenderá isso melhor ao ler a próxima seção.
Antes de passarmos a ela, vamos testar seu entendimento com a seguinte pergunta. A resposta será encontrada nas próximas seções, basta seguir lendo.
Pergunta: uma imagem é representada por um array de pixels bidimensional. Se você usar um laço for aninhado para iterar por cada pixel (ou seja, se tiver um laço for para todas as colunas, e outro laço for interno para todas as linhas), qual será a complexidade de tempo do algoritmo quando a imagem é considerada como a entrada?
3. Big O, Little O, Omega e Theta
Big O: "f(n) é O(g(n))" se e somente se, para algumas constantes c e N₀, f(N) ≤ cg(N) para todos N > N₀
Omega: "f(n) é Ω(g(n))" se e somente se, para algumas constantes c e N₀, f(N) ≥ cg(N) para todos N > N₀
Theta: "f(n) é Θ(g(n))" se e somente se f(n) for O(g(n)) e f(n) for Ω(g(n))
Little O: "f(n) é o(g(n))" se e somente se f(n) for O(g(n)) e f(n) não for Θ(g(n))
—Definição formal de Big O, Omega, Theta e Little O
Simplificando:
- Big O (O()) descreve o limite superior da complexidade.
- Omega (Ω()) descreve o limite inferior da complexidade.
- Theta (Θ()) descreve o limite exato da complexidade.
- Little O (o()) descreve o limite superior excluindo o limite exato.
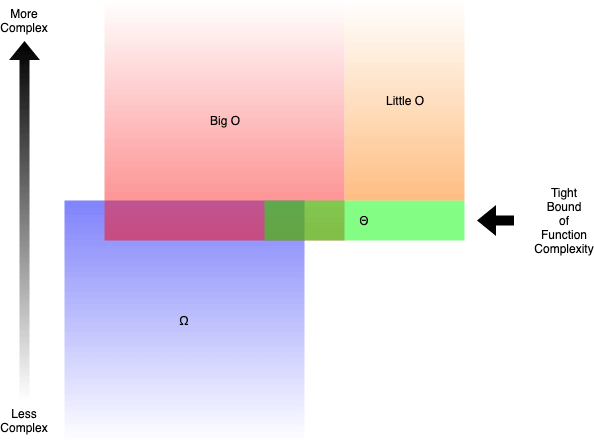
Por exemplo, a função g(n) = n² + 3n é O(n³), o(n⁴), Θ(n²) e Ω(n). Mas você estaria correto se dissesse que é Ω(n²) ou O(n²).
Em geral, quando falamos de Big O, o que se está falando de fato é de Theta. Não faz sentido dar um limite superior que é muito maior que o escopo da análise. Seria semelhante a resolver inequações colocando ∞ no lado maior, o que quase sempre faz com que você esteja certo.
Mas como determinamos quais funções são mais complexas que as outras? Na próxima seção que você lerá, aprenderemos isso em detalhes.
4. Comparação de complexidade entre Big Os típicas
Quando tentamos descobrir a Big O para uma função g(n) específica, nos preocupamos apenas com o termo dominante da função. O termo dominante é o termo que cresce mais rápido.
Por exemplo, n² cresce mais rápido que n. Assim, se tivermos algo como g(n) = n² + 5n + 6, teremos uma big O(n²). Se você já fez cálculo no passado, isso é muito semelhante a achar o atalho para encontrar limites para polinômios fracionários, onde você só se importa com o termo dominante para numeradores e denominadores no fim.

Mas qual função cresce mais rápido do que as outras? Existem, de fato, algumas regras.
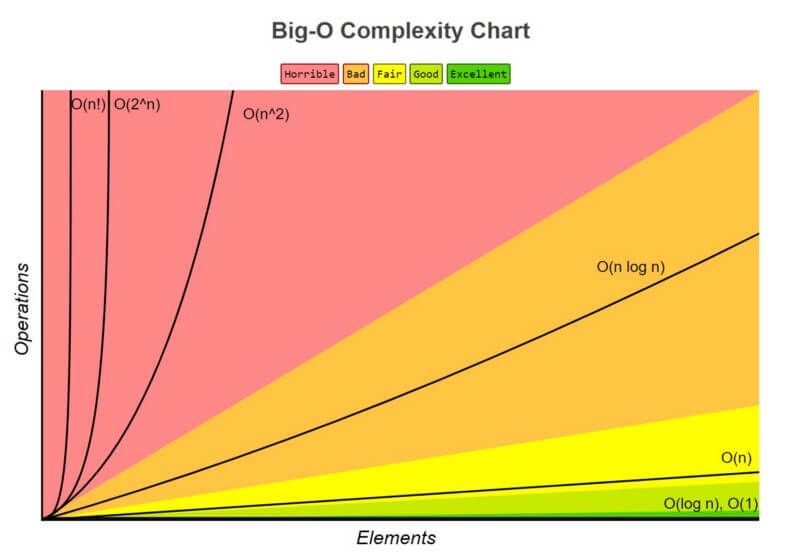
1. O(1) tem a menor complexidade
Geralmente chamado de "tempo constante", se você pode criar um algoritmo para resolver o problema em O(1), isso é normalmente o melhor que você pode conseguir. Em alguns cenários, a complexidade pode passar de O(1), então podemos analisá-la encontrando sua contrapartida O(1/g(n)). Por exemplo, O(1/n) é mais complexo do que O(1/n²).
2. O(log(n)) é mais complexo do que O(1), mas menos complexo do que polinômios
Como a complexidade geralmente está associada a algoritmos de dividir e conquistar, O(log(n)) costuma ser uma complexidade boa que você pode alcançar em algoritmos de ordenação. O(log(n)) é menos complexo que O(√n), pois a função da raiz quadrada pode ser considerada um polinômio, onde o expoente é 0,5.
3. A complexidade dos polinômios aumenta de acordo com o aumento do expoente
Por exemplo, O(n⁵) é mais complexo que O(n⁴). Devido à simplicidade disso, passamos por vários exemplos de polinômios nas seções anteriores.
4. Exponenciais têm maior complexidade do que polinômios, contanto que os coeficientes sejam múltiplos positivos de n
O(2ⁿ) é mais complexo que O(n⁹⁹), mas O(2ⁿ) é, de fato, menos complexo que O(1). Geralmente usamos 2 como a base para exponenciais e logaritmos porque as coisas tendem a ser binárias em Ciência da Computação, mas os expoentes podem ser alterados mudando-se os coeficientes. Se não estiver especificada, assume-se que a base para os logaritmos seja 2.
5. Fatoriais têm complexidade maior do que exponenciais
Se tiver interesse no motivo para isso, consulte a função Gama, que é uma extensão analítica de um fatorial. Uma pequena prova disso é que fatoriais e exponenciais têm o mesmo número de multiplicações, mas os números que são multiplicados crescem para os fatoriais, mas permanecem constantes para as exponenciais.
6. Termos multiplicadores
Ao multiplicar, a complexidade será maior que a original, mas não mais que a equivalência de multiplicar algo que é mais complexo. Por exemplo, O(n * log(n)) é mais complexo que O(n), mas menos complexo do que O(n²), pois O(n²) = O(n * n) e n é mais complexo do que log(n).
Para testar sua compreensão, tente classificar as funções a seguir da mais complexa para a menos complexa. As soluções com explicações detalhadas podem ser encontradas em uma seção posterior quando você chegar lá. Algumas delas tendem a ser traiçoeiras e podem exigir uma compreensão maior da matemática. Ao chegar à solução, você as entenderá melhor.
Pergunta: classifique as funções abaixo, da mais complexa para a menos complexa.
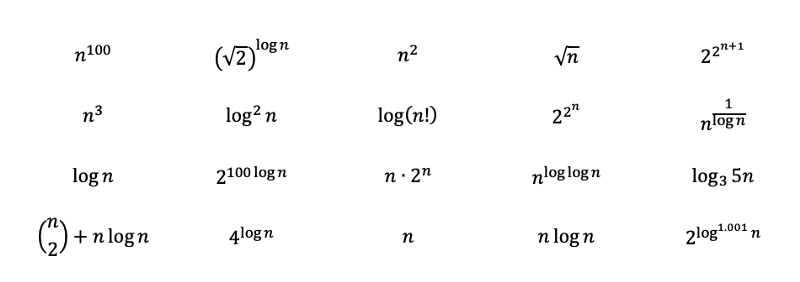
Solução para a pergunta da seção 2:
Era para ser de fato uma pergunta traiçoeira para testar seu entendimento. A questão tenta fazer com que você responda O(n²), pois há um laço for aninhado. Porém, n deve ser o tamanho da entrada. Como o array da imagem é a entrada, e como cada pixel foi iterado apenas uma vez, a resposta de fato é O(n). Na próxima seção, você verá mais exemplos como esse.
5. Complexidade de espaço e de tempo
Até o momento, só discutimos a complexidade de tempo dos algoritmos. Ou seja, só nos preocupamos com o tempo que leva para o programa completar a tarefa. O que também importa é o espaço que o programa leva para completar a tarefa. A complexidade de espaço é relacionada com o quanto de memória o programa usará e, portanto, também é um fator importante a ser analisado.
A complexidade de espaço funciona de modo semelhante à complexidade de tempo. Por exemplo, a selection sort tem uma complexidade de espaço de O(1), porque ela somente armazena um valor mínimo e seu índice para comparação, o espaço máximo usado não aumenta com o tamanho da entrada.
Alguns algoritmos, como a bucket sort, tem uma complexidade de espaço de O(n), mas pode reduzir a complexidade de tempo para O(1). A bucket sort ordena o array criando uma lista ordenada de todos os elementos possíveis no array, depois incrementa o contador sempre que um elemento é encontrado. No fim, o array ordenado serão os elementos da lista ordenada repetidos por suas contagens.
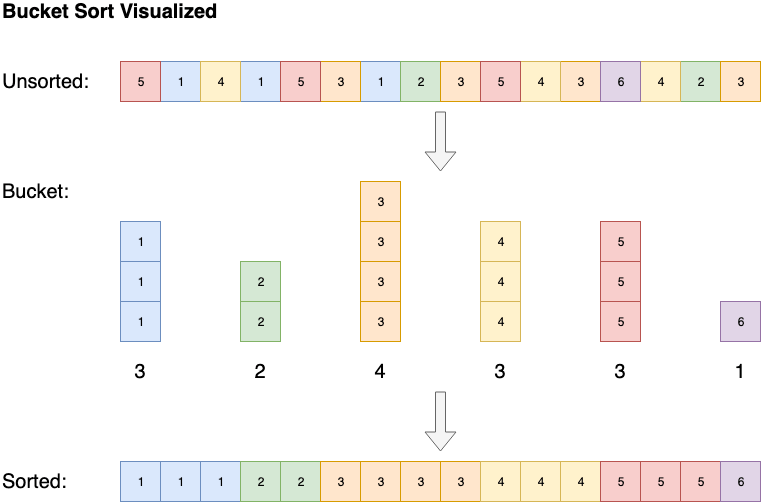
6. Complexidade ideal, média, de pior caso e esperada
A complexidade também será analisada como a ideal, de pior caso, média e esperada.
Vejamos a insertion sort, por exemplo. A insertion sort itera por todos os elementos da lista. Se o elemento for menor que o elemento anterior, ela insere o elemento antes do outro elemento até que ele seja maior que o elemento anterior.
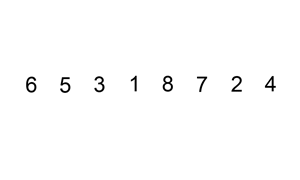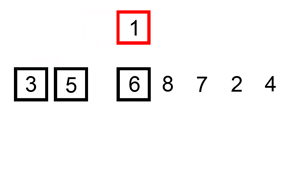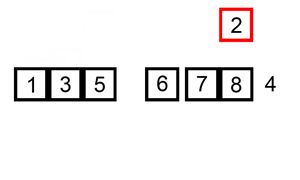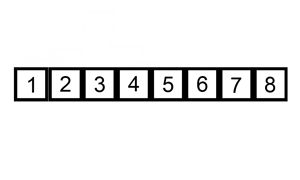
Se o array já estiver ordenado inicialmente, não haverá trocas. O algoritmo vai iterar pelo array apenas uma vez, o que resulta em uma complexidade de O(n). Portanto, diríamos que a complexidade de tempo de melhor caso da insertion sort é O(n). Uma complexidade de O(n) também é conhecida normalmente como complexidade linear.
Algumas vezes, o algoritmo simplesmente tem má sorte. A quick sort, por exemplo, terá de percorrer a lista no tempo O(n) se os elementos forem ordenados na ordem oposta, mas, na média, ele ordena o array no tempo O(n * log(n)). Em geral, quando avaliamos a complexidade de tempo de um algoritmo, vemos o seu desempenho no pior dos casos. Mais sobre isso e sobre a quick sort será discutido na próxima seção quando você chegar lá.
A complexidade média descreve o desempenho esperado do algoritmo. Algumas vezes, isso envolve calcular a probabilidade de cada cenário. Pode ser complicado entrar em detalhes e, por isso, não discutimos essa questão neste artigo. Abaixo temos uma ficha informativa da complexidade de tempo e de espaço dos algoritmos típicos.
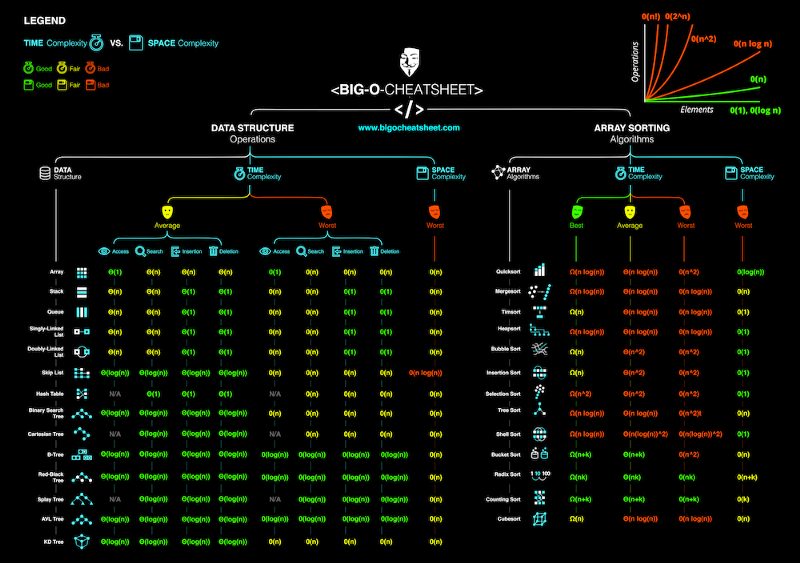
Solução para a pergunta da seção 4:
Ao inspecionar as funções, poderemos classificar imediatamente os seguintes polinômios do mais complexo para o menos complexo com a regra 3. Nela, a raiz quadrada de n é simplesmente n na potência 0,5.
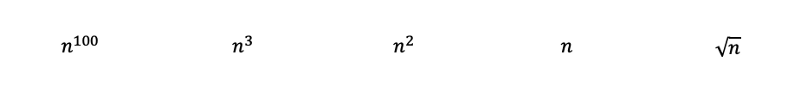
Então, ao aplicar as regras 2 e 6, temos o seguinte. O log de base 3 pode ser convertido na base 2 com a mudança de base dos logaritmos. O log de base 3 ainda cresce um pouco mais lentamente do que os logs de base 2, vindo, desse modo, classificado depois.
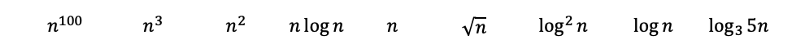
O resto pode parecer um pouco mais difícil, mas vamos tentar desvendar os mistérios e ver onde podemos colocá-los.
Primeiro, 2 na potência 2 na potência n é maior do que 2 na potência n. O +1 dá um tempero ainda maior.

E já que sabemos que 2 na potência log(n) com base 2 é igual a n, podemos converter o seguinte. O log com 0.001 como expoente cresce um pouco mais do que as constantes, mas menos do que qualquer outra coisa.

Aquele termo com n na potência log(log(n)) é de fato uma variação do tempo quasi-polinomial, que é maior do que o polinômio, mas menor que a exponencial. Como log(n) cresce mais lento do que n, a complexidade dele é um pouco menor. Aquele termo com o log invertido converge para constante, pois 1/log(n) diverge para o infinito.

Os fatoriais podem ser representados por multiplicações, podendo ser convertidos para adições fora da função logarítmica. "n seleção de 2" pode ser convertido em um polinômio com um termo cúbico sendo o maior.

Finalmente, podemos classificar as funções da mais complexa para a menos complexa.
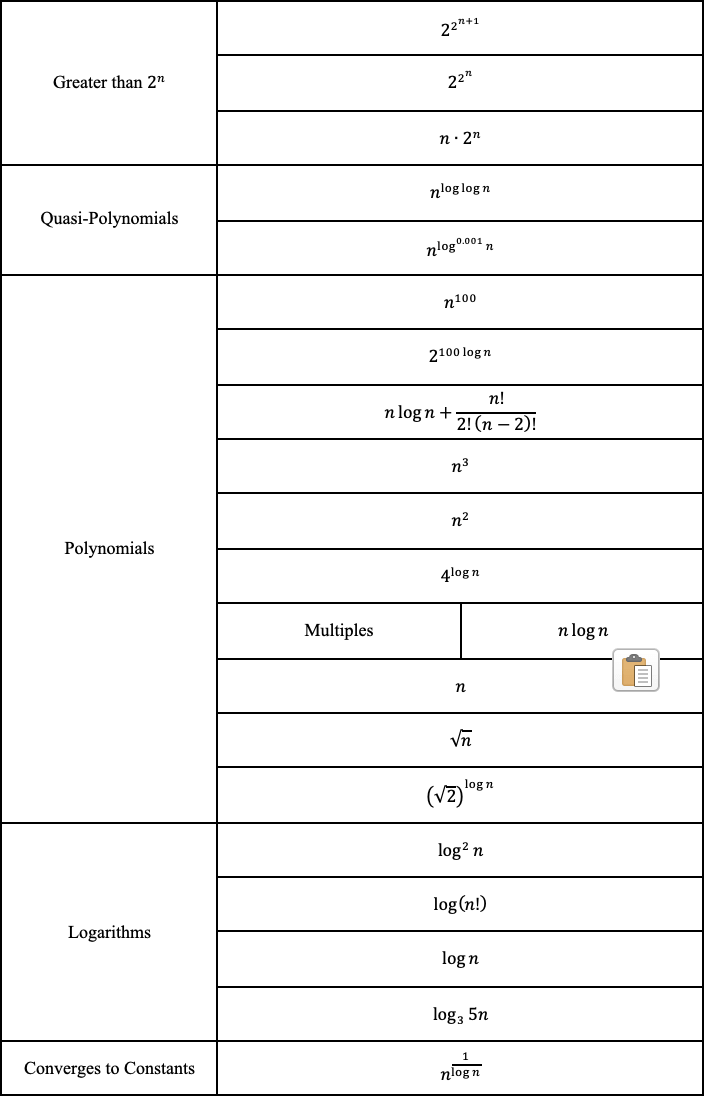
Por que a Big O não importa
!!! — AVISO — !!!
O conteúdo discutido aqui geralmente não é aceito pela maioria dos programadores do mundo. Discuta o assunto por sua conta e risco em uma entrevista. Já houve quem publicasse em um blog sobre como não tiveram sucesso em entrevistas para a Google por terem questionado a autoridade, como ocorre aqui.
!!! — AVISO — !!!
Como aprendemos anteriormente que a complexidade de tempo de pior caso para a quick sort é de O(n²), mas de O(n * log(n)) para a merge sort, esta última deve ser mais rápida, certo? Você provavelmente deve ter adivinhado que a resposta é falsa. Os algoritmos simplesmente foram construídos de um modo que torna a quick sort... "rápida".
Para demonstrar, confira este trinket.io que eu fiz. Ele compara o tempo para a quick sort e a merge sort. Eu só consegui testar isso em arrays de comprimento menor ou igual a 10000, mas, como você pode ver até o momento, o tempo da merge sort cresce mais rápido do que o da quick sort. Embora a quick sort tenha uma complexidade de O(n²) no pior caso, a probabilidade de ele acontecer é realmente muito baixa. Quando se trata do aumento de velocidade que a quick sort tem com relação à merge sort, limitada pela complexidade O(n * log(n)) , a quick sort acaba tendo um desempenho melhor, em média.
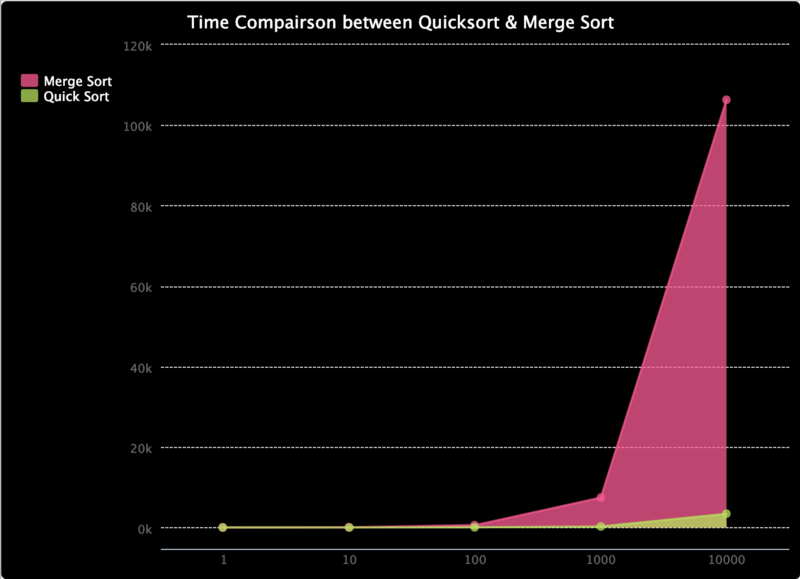
Eu também fiz o gráfico abaixo para comparar a proporção entre o tempo que elas levam, já que é difícil vê-las em valores mais baixos. Como você pode ver, a porcentagem de tempo necessário para a quick sort está em ordem descendente.
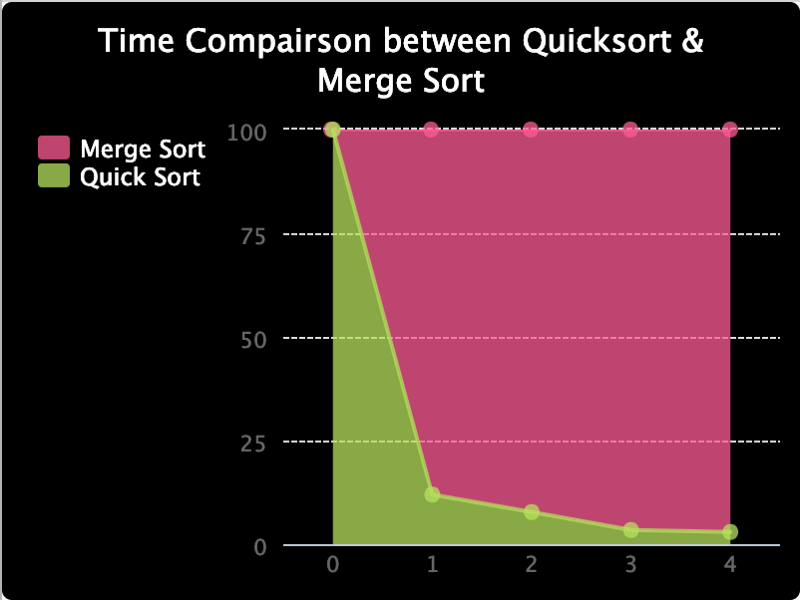
A moral da história é que a notação Big O é apenas uma análise matemática para fornecer uma referência com relação aos recursos consumidos por um algoritmo. Na prática, os resultados podem ser diferentes. É, no entanto, uma boa prática tentar reduzir ao máximo a complexidade dos nossos algoritmos, até chegarmos a um caso em que sabemos o que estamos fazendo.
No fim das contas…
Eu gosto de programar, de aprender coisas novas e de compartilhá-las com a comunidade. Se há algo que interessa você em especial, mande-me uma mensagem. Eu geralmente escrevo sobre design para a web, arquitetura de software, matemática e ciência de dados. Você pode encontrar alguns arquivos ótimos que escrevi no passado se estiver interessado em qualquer um dos tópicos acima.
Espero que você aproveite ao máximo o aprendizado em Ciência da Computação!!!

