Tudo o que você precisa saber sobre estruturas de dados em árvore

Artigo original: Everything you need to know about tree data structures

Quando você aprende a programar pela primeira vez, é comum aprender arrays como a "principal estrutura de dados".

Em algum momento, você também aprenderá sobre tabelas hash. Se você estiver buscando o diploma em Ciência da Computação, você terá que fazer uma disciplina de estrutura de dados. Você também aprenderá sobre listas vinculadas, filas e pilhas. Essas estruturas de dados são chamadas de estruturas de dados "lineares", pois todas elas têm um início e um fim lógicos.

Quando começamos a aprender sobre árvores e grafos, pode ficar bastante confuso. Neles, não armazenamos dados de forma linear. As duas estruturas armazenam dados de um modo específico.

Este artigo é para ajudá-lo a entender melhor a estrutura de dados de árvore e para esclarecer qualquer confusão que você possa ter sobre ela.

Nele, vamos aprender:

• O que é uma árvore
• Exemplos de árvore
• Sua terminologia e como ela funciona
• Como implementar estruturas de árvore em código.

Vamos começar esta jornada de aprendizagem :)

Definição

Ao começar a programar, é comum entender melhor as estruturas de dados lineares do que estruturas de dados como árvores e grafos.

As árvores são conhecidas como uma estrutura de dados não linear. Elas não armazenam dados de modo linear. Elas organizam os dados de modo hierárquico.

Vamos examinar exemplos da vida real!

O que quero dizer quando digo de modo hierárquico?

Imagine uma árvore genealógica com relacionamentos de todas as gerações: avós, pais, filhos, irmãos e assim por diante. Geralmente, organizamos as árvores genealógicas de modo hierárquico.

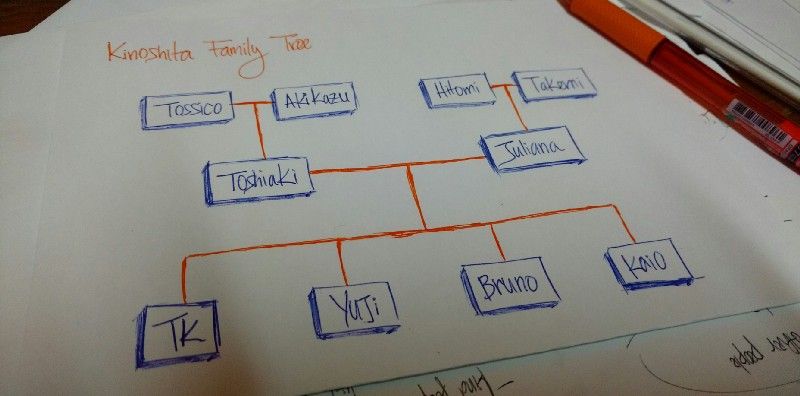
O desenho acima é a minha árvore genealógica. Tossico, Akikazu, Hitomi e Takemi são meus avós.

Toshiaki e Juliana são meus pais.

TK, Yuji, Bruno e Kaio são os filhos dos meus pais (eu e meus irmãos).

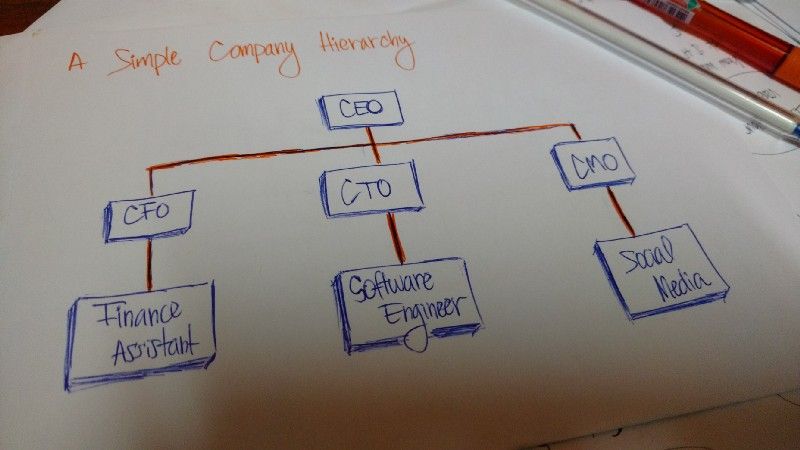
A estrutura de uma organização é outro exemplo de uma hierarquia.

Em HTML, o Modelo de Objeto de Documento (em inglês, DOM, ou Document Object Model) funciona como uma árvore.

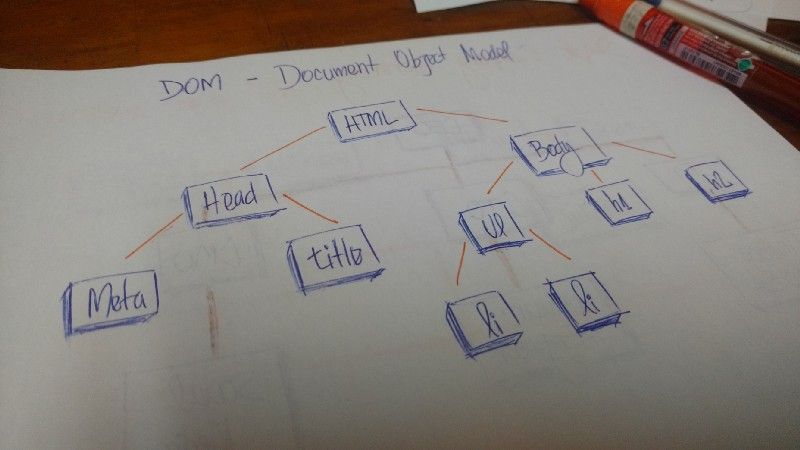
A tag HTML contém outras tags. Temos uma tag head e uma tag body. Essas tags contêm elementos específicos. A tag head tem tags meta e tags title. A tag body tem elementos que aparecem na interface do usuário, como h1, a, li, entre outros.

Uma definição técnica

Uma árvore é um conjunto de entidades chamadas nós. Os nós são conectados por arestas. Cada nó contém um valor ou dados e pode ou não ter um nó filho.

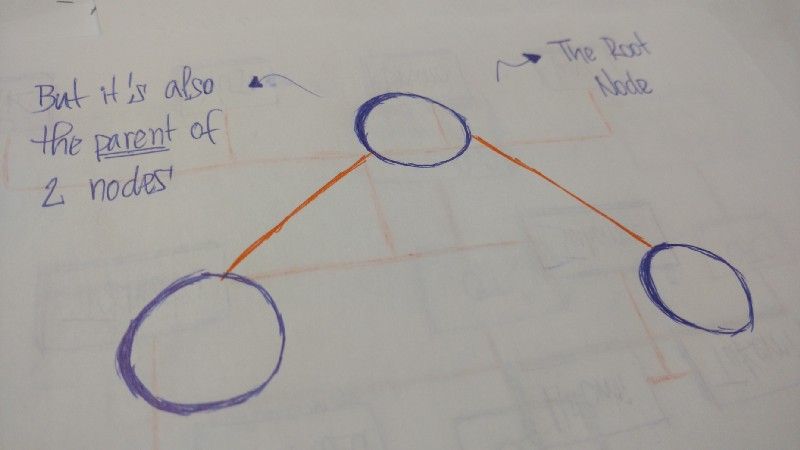
O primeiro nó da árvore é chamado de raiz. Se este nó raiz é conectado por outro nó, a raiz é então um nó pai e o nó conectado é um nó filho.

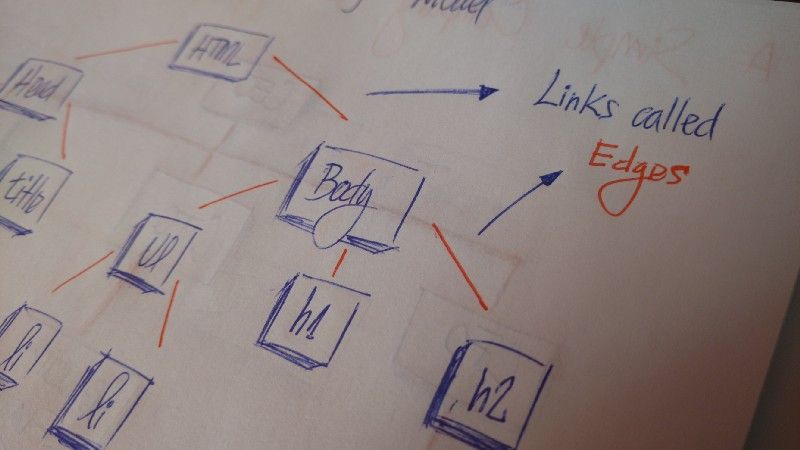
Todos os nós das árvores são conectados por links chamados arestas. Essa é uma parte importante das árvores, porque elas gerenciam a relação entre os nós.

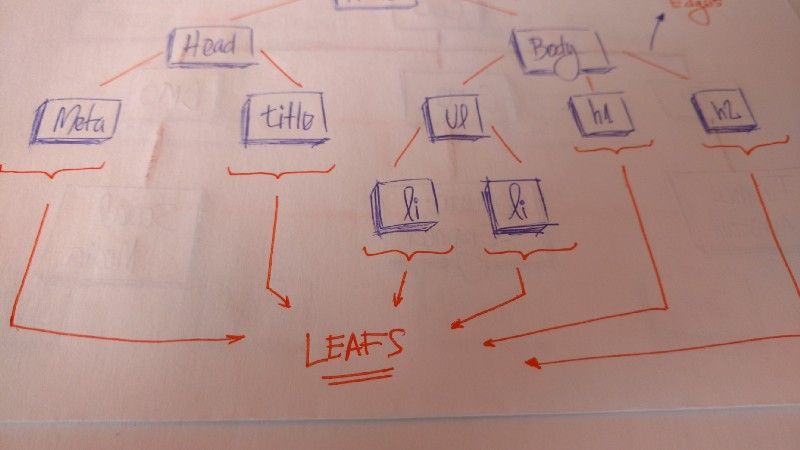
As folhas são os últimos nós de uma árvore. Elas são os nós sem filhos. Como árvores reais, temos a raiz, os ramos e, finalmente, as folhas.

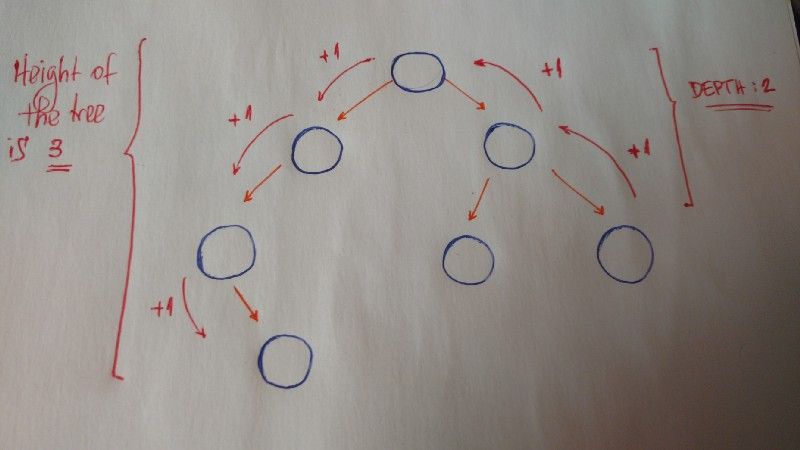
Outros conceitos importantes a serem entendidos são altura e profundidade.

A altura de uma árvore é o tamanho do caminho mais longo até uma folha.

A profundidade de um nó é o tamanho do caminho percorrido do nó até a raiz.

Resumo da terminologia

• A raiz é o nó mais alto da árvore
• A aresta é a ligação entre dois nós
• O filho é um nó que tem um nó pai
• O pai é um nó que tem uma aresta apontando para um nó filho
• A folha é um nó que não tem nós filhos na árvore
• A altura é o tamanho do caminho mais longo até uma folha
• A profundidade é o tamanho do caminho percorrido do nó até a raiz

Árvores binárias

Agora, vamos discutir um tipo específico de árvore. Nós a chamamos de árvore binária.

"Na ciência da computação, uma árvore binária é uma estrutura de dados em árvore na qual cada nó tem, no máximo, dois filhos, que são referidos como o filho da esquerda e o filho da direita". - Wikipédia

Então, vejamos um exemplo de árvore binária.

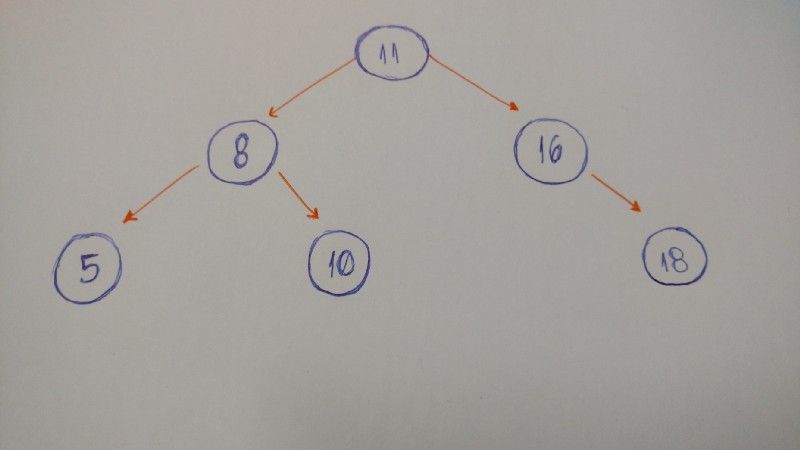
Vamos programar uma árvore binária

A primeira coisa que precisamos ter em mente quando implementamos uma árvore binária é o fato de ela ser uma coleção de nós. Cada nó tem três atributos: value, left_child (o filho da esquerda) e right_child (o filho da direita).

Como implementamos uma árvore binária simples que inicializa com estas três propriedades?

Vamos dar uma olhada.

class BinaryTree:
    def __init__(self, value):
        self.value = value
        self.left_child = None
        self.right_child = None

Aqui está. Esta é a nossa classe de árvore binária.

Quando instanciamos um objeto, passamos value (os dados do nó) como um parâmetro. Olhe para left_child e para right_child. Os dois estão definidos como None (Nenhum).

Por quê?

Porque quando criamos nosso nó, ele não tem filhos. Temos apenas os dados do nó.

Vamos testá-lo:

tree = BinaryTree('a')
print(tree.value) # a
print(tree.left_child) # None
print(tree.right_child) # None

É isso.

Podemos passar a string 'a' como o valor para nosso nó da árvore binária. Se imprimirmos value, left_child e right_child, podemos ver os valores.

Vamos para a parte de inserção. O que precisamos fazer aqui?

Vamos implementar um método para inserir um novo nó à direita e à esquerda.

Aqui estão as regras:

• Se o nó atual não tiver um filho da esquerda, criamos apenas um nó e o configuramos como left_child do nó atual.
• Se ele tiver o filho da esquerda, criamos um nó e o colocamos no lugar da filho da esquerda atual. Alocamos este nó filho da esquerda como o novo nó left_child.

Vamos representar isso com um desenho :)

Aqui está o código:

def insert_left(self, value):
    if self.left_child == None:
        self.left_child = BinaryTree(value)
    else:
        new_node = BinaryTree(value)
        new_node.left_child = self.left_child
        self.left_child = new_node

Novamente, se o nó atual não tiver um filho da esquerda, apenas criamos um nó e o configuramos como left_child do nó atual. Como alternativa, criamos um nó e o colocamos no lugar do left_child atual. Alocamos este nó como o novo nó left_child.

Fazemos a mesma coisa para inserir um nó do filho da direita.

def insert_right(self, value):
    if self.right_child == None:
        self.right_child = BinaryTree(value)
    else:
        new_node = BinaryTree(value)
        new_node.right_child = self.right_child
        self.right_child = new_node

Feito. :)

Porém, temos que testá-lo.

Vamos construir a seguinte árvore:

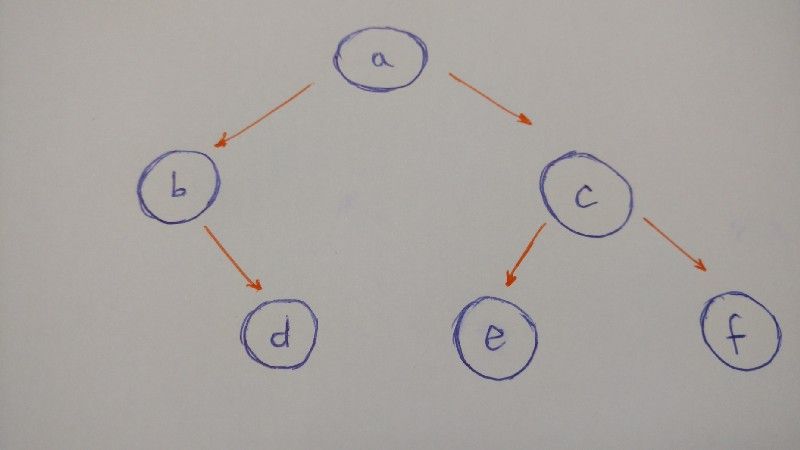
Para resumir a ilustração desta árvore:

• o nó a será a raiz da nossa árvore binária
• o filho da esquerda de a é o nó b
• o filho da direita de a é o nó c
• o filho da direita de b é o nó d (o nó b não tem um filho da esquerda)
• o filho da esquerda de c é o nó e
• o filho da direita de c é o nó f
• tanto o nó e como o nó f não têm filhos

Portanto, aqui está o código para a árvore:

a_node = BinaryTree('a')
a_node.insert_left('b')
a_node.insert_right('c')

b_node = a_node.left_child
b_node.insert_right('d')

c_node = a_node.right_child
c_node.insert_left('e')
c_node.insert_right('f')

d_node = b_node.right_child
e_node = c_node.left_child
f_node = c_node.right_child

print(a_node.value) # a
print(b_node.value) # b
print(c_node.value) # c
print(d_node.value) # d
print(e_node.value) # e
print(f_node.value) # f

A inserção está feita.

Agora temos que pensar na travessia da árvore.

Temos aqui duas opções: a Busca em Profundidade (DFS - Depth-First Search) e a Busca em Largura (BFS - Breadth-First Search).

• DFS "é um algoritmo para fazer uma travessia ou pesquisar a estrutura de dados em árvore. Ele começa pela raiz e explora o máximo possível ao longo de cada ramo antes de retroceder". – Wikipedia
• BFS "é um algoritmo para fazer uma travessia ou pesquisar a estrutura de dados em árvore. Ele começa na raiz da árvore e explora os nós vizinhos primeiro antes de passar para os vizinhos do nível seguinte". – Wikipedia

Portanto, vamos analisar os tipos de travessia de árvores.

Busca em Profundidade (DFS - Depth-First Search)

A DFS explora todo um caminho até uma folha antes de retroceder (backtracking) e explorar outro caminho. Vamos dar uma olhada em um exemplo com este tipo de travessia.

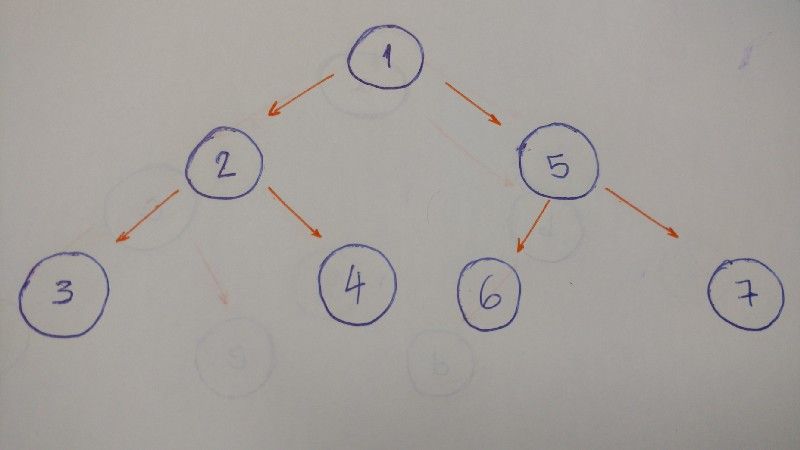
O resultado para este algoritmo será 1–2–3–4–5–6–7.

Por quê?

Vamos dividi-lo em partes.

1. Comece na `raiz` (1). Imprima-a.

2. Vá para o filho da esquerda (2). Imprima-o.

3. Então, vá para o filho da esquerda (3). Imprima-o. (Este nó não tem filhos)

4. Retroceda e vá para filho da direita (4). Imprima-o. (Este nó não tem filhos)

5. Retroceda, vá para nó raiz e vá para o filho da direita (5). Imprima-o.

6. Vá para o filho da esquerda (6). Imprima-o. (Este nó não tem filhos)

7. Retroceda e vá para filho da direita (7). Imprima-o. (Este nó não tem filhos)

8. Feito.

Quando vamos a fundo até uma folha e retrocedemos, isso é chamado de algoritmo DFS.

Agora que estamos familiarizados com esse algoritmo de travessia, discutiremos os tipos de DFS: pré-ordem, em ordem e pós-ordem.

Pré-ordem

Isso é exatamente o que fizemos no exemplo acima.

1. Imprimir o valor do nó.
2. Ir para o filho da esquerda e imprimi-lo se, e somente se, tiver um filho da esquerda.
3. Ir para o filho da direita e imprimi-lo se, e somente se, tiver um filho da direita.

def pre_order(self):
    print(self.value)

    if self.left_child:
        self.left_child.pre_order()

    if self.right_child:
        self.right_child.pre_order()

Em ordem

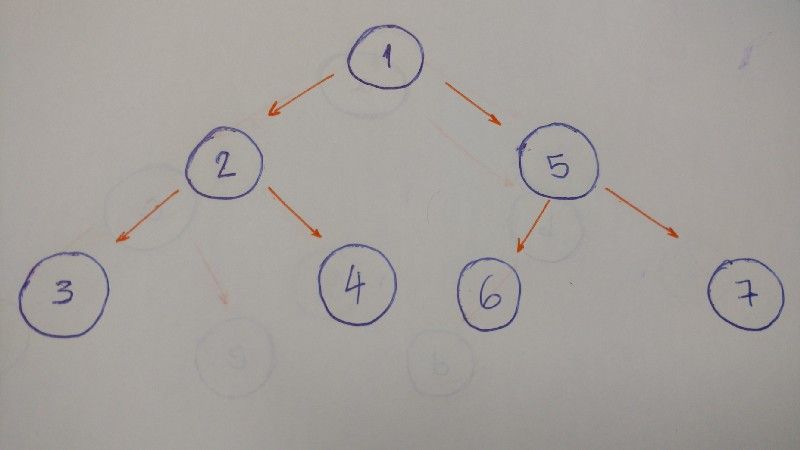
O resultado do algoritmo em ordem para este exemplo da árvore é 3–2–4–1–6–5–7.

Começamos da esquerda primeiro, depois pegamos o do meio e, por fim, o da direita.

Agora, vamos transformar isso em código.

def in_order(self):
    if self.left_child:
        self.left_child.in_order()

    print(self.value)

    if self.right_child:
        self.right_child.in_order()

1. Vá para o filho da esquerda e imprima-o se, e somente se, tiver um filho da esquerda.
2. Imprima o valor do nó
3. Vá para o filho da direita e imprima-o se, e somente se, tiver um filho da direita.

Pós-ordem

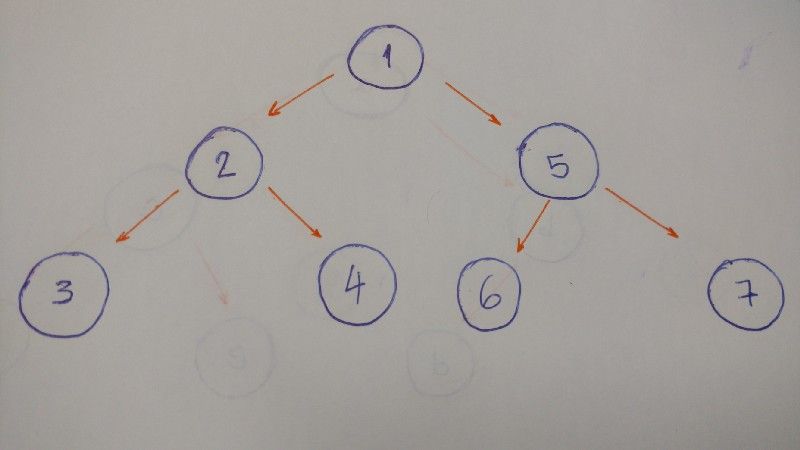
O resultado do algoritmo de pós-ordem para este exemplo de árvore é 3–4–2–6–7–5–1.

Começamos com a esquerda, seguindo da direita e depois o meio.

Vamos transformar isso em código.

def post_order(self):
    if self.left_child:
        self.left_child.post_order()

    if self.right_child:
        self.right_child.post_order()

    print(self.value)

1. Vá para o filho da esquerda e imprima-o se, e somente se, tiver um filho da esquerda.
2. Vá até o filho da direita e imprima-o se, e somente se, tiver um filho da direita.
3. Imprima o valor do nó

Busca em largura (BFS - Breadth-First Search)

O algoritmo BFS atravessa a árvore nível por nível e profundidade por profundidade.

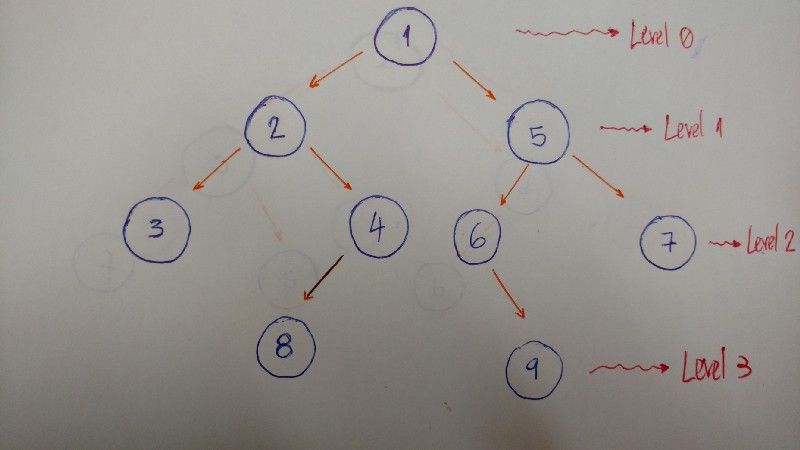
Aqui está um exemplo que ajuda a explicar melhor este algoritmo:

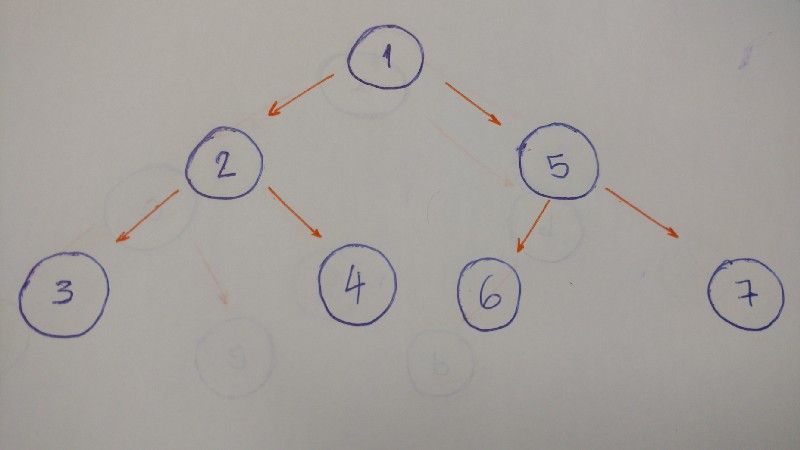
Portanto, atravessamos nível por nível. Neste exemplo, o resultado é 1–2–5–3–4–6–7.

• Nível/Profundidade 0: somente o nó com valor 1
• Nível/Profundidade 1: nós com valores 2 e 5
• Nível/Profundidade 2: nós com valores 3, 4, 6, e 7

Agora, vamos transformar isso em código.

def bfs(self):
    queue = Queue()
    queue.put(self)

    while not queue.empty():
        current_node = queue.get()
        print(current_node.value)

        if current_node.left_child:
            queue.put(current_node.left_child)

        if current_node.right_child:
            queue.put(current_node.right_child)

Para implementar um algoritmo de BFS, usamos a estrutura de dados da fila para ajudar.

Como funciona?

Aqui está a explicação.

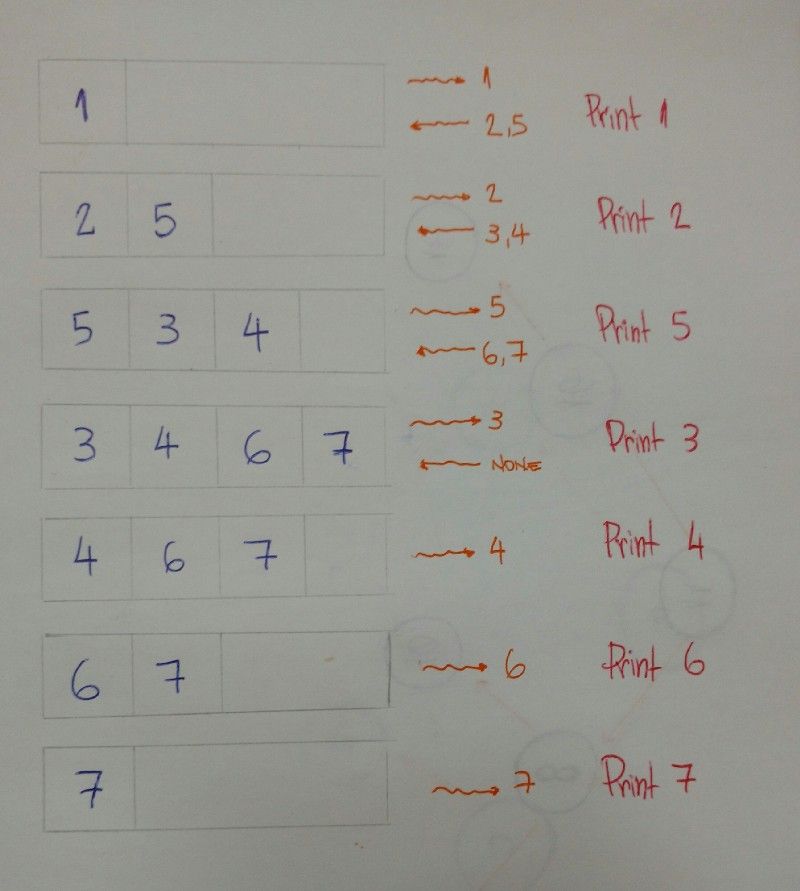
1. Primeiro adicione o nó raiz na fila (Queue) com o método put.
2. Itere enquanto a fila não estiver vazia.
3. Obtenha o primeiro nó na fila, depois imprima o seu valor.
4. Acrescentar o filho da esquerda e o filho da direita na fila (se o nó atual tiver filhos).
5. Feito. Imprimiremos o valor de cada nó, nível por nível, com nosso ajudante de fila.

Árvore binária de busca

"Uma árvore binária de busca é às vezes chamada de árvore binária ordenada ou classificada, e mantém seus valores em ordem, para que a busca e as outras operações possam usar o princípio da busca binária" - Wikipedia

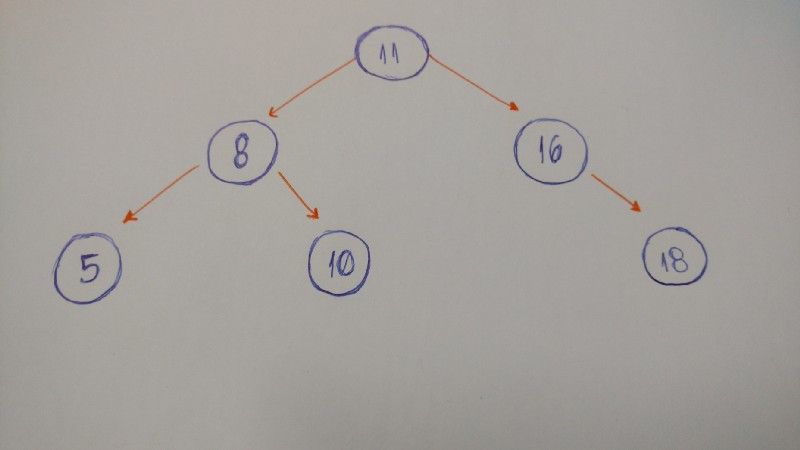
Uma propriedade importante de uma árvore binária de busca é que o valor de um nó da árvore binária de busca é maior que o valor dos descendentes do seu filho da esquerda, mas menor que o valor dos descendentes de seu filho da direita".

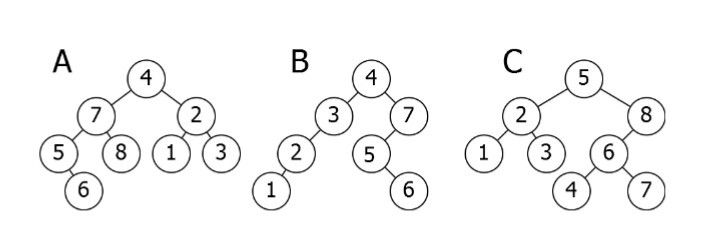
Aqui está uma descrição da ilustração acima:

• A está invertido. A subárvore 7-5-8-6 precisa estar do lado direito e a subárvore 2-1-3 precisa estar do lado esquerdo.
• B é a única opção correta. Ela satisfaz a propriedade da árvore binária de busca.
• C tem um problema: o nó com o valor 4. Ele precisa estar do lado esquerdo da raiz porque é menor do que 5.

Vamos programar uma árvore de busca binária!

Agora é hora de programar!

O que veremos aqui? Vamos inserir novos nós, procurar um valor, deletar nós e o equilíbrio da árvore.

Vamos começar.

Inserção: adicionar novos nós à nossa árvore

Imagine que temos uma árvore vazia e que queremos adicionar novos nós com os seguintes valores nesta ordem: 50, 76, 21, 4, 32, 100, 64, 52.

A primeira coisa que precisamos saber é se 50 é a raiz de nossa árvore.

Podemos agora começar a inserir nó por nó.

• 76 é maior que 50, portanto insira 76 no lado direito.
• 21 é menor do que 50, portanto insira 21 no lado esquerdo.
• 4 é menor do que 50. O nó com valor 50 tem um filho da esquerda 21. Como 4 é menor do que 21, insira-o no lado esquerdo deste nó.
• 32 é menor do que 50. O nó com valor 50 tem um filho da esquerda 21. Como 32 é maior que 21, insira 32 no lado direito deste nó.
• 100 é maior que 50. O nó com valor 50 tem um filho da direita 76. Como 100 é maior que 76, insira 100 no lado direito deste nó.
• 64 é maior que 50. O nó com valor 50 tem um filho da direita 76. Como 64 é menor que 76, insira 64 no lado esquerdo deste nó.
• 52 é maior que 50. O nó com valor 50 tem um filho da direita 76. Como 52 é menor do que 76, o nó com valor 76 tem um filho da esquerda 64. 52 é menor do que 64, portanto insira 54 no lado esquerdo deste nó.

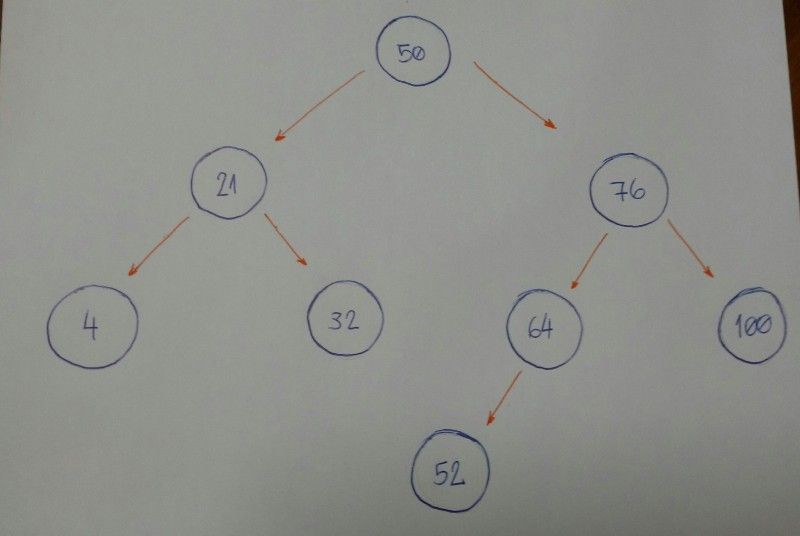
Você percebe um padrão aqui?

Vamos analisar.

1. O valor do novo nó é maior ou menor que o do nó atual?
2. Se o valor do novo nó for maior que o nó atual, vá para a subárvore à direita. Se o nó atual não tiver um filho da direita, insira-o lá ou retroceda para o passo nº 1.
3. Se o valor do novo nó for menor do que o nó atual, vá para a subárvore à esquerda. Se o nó atual não tiver um filho da esquerda, insira-o lá ou retroceda para o passo nº 1.
4. Não tratamos de casos especiais aqui. Quando o valor de um novo nó for igual ao valor atual do nó, use a regra número 3. Considere a inserção de valores iguais no lado esquerdo da subárvore.

Agora vamos transformar isso em código.

class BinarySearchTree:
    def __init__(self, value):
        self.value = value
        self.left_child = None
        self.right_child = None

    def insert_node(self, value):
        if value <= self.value and self.left_child:
            self.left_child.insert_node(value)
        elif value <= self.value:
            self.left_child = BinarySearchTree(value)
        elif value > self.value and self.right_child:
            self.right_child.insert_node(value)
        else:
            self.right_child = BinarySearchTree(value)

Parece muito simples.

A parte poderosa desse algoritmo é a parte de recursão, que está nas linhas 9 e 13. As duas linhas de código chamam o método insert_node e o utilizam para seus filhos à esquerda e filhos à direita, respectivamente. As linhas 11 e 15 são as que fazem a inserção para cada filho.

Vamos procurar o valor do nó... ou não...

O algoritmo que construiremos agora é o de buscas. Para um determinado valor (número inteiro), diremos se nossa árvore de busca binária tem ou não esse valor.

Um item importante a ser observado é como definimos o algoritmo de inserção de árvores. Primeiro, temos nosso nó raiz. Todos os nós da subárvore da esquerda terão valores menores que o nó raiz. Todos os nós da subárvore da direita terão valores maiores que o nó raiz.

Vamos dar uma olhada em um exemplo.

Imagine que temos esta árvore.

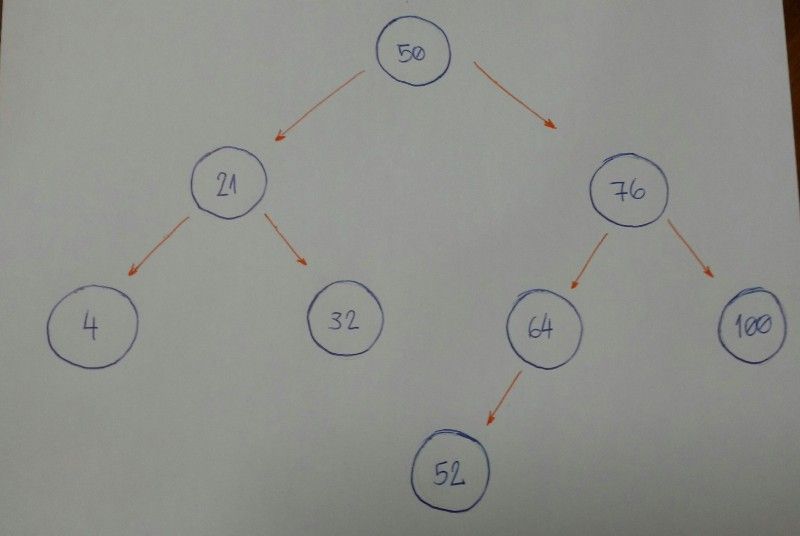
Agora, queremos saber se temos um nó baseado no valor 52.

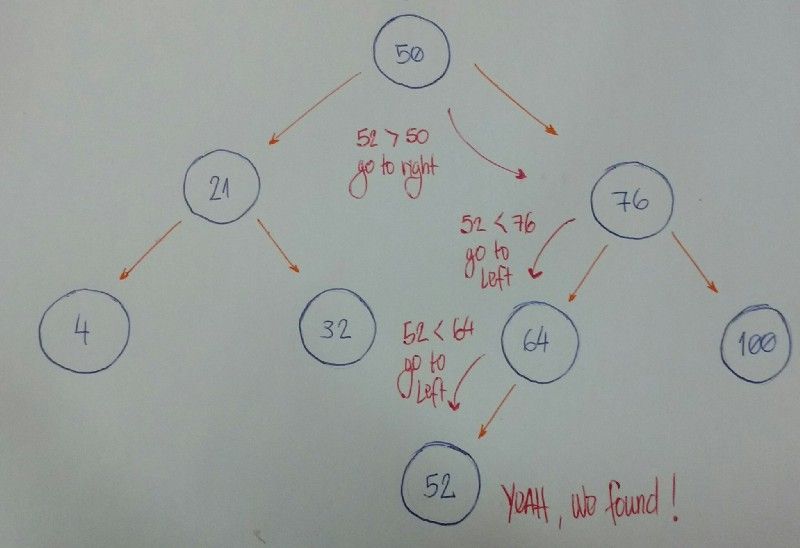
Vamos analisar.

1. Começamos com o nó raiz como nosso nó atual. O valor dado é menor do que o valor do nó atual? Se sim, buscaremos esse valor na subárvore da esquerda.
2. O valor dado é maior do que o valor do nó atual? Se sim, buscaremos esse valor na subárvoreda direita.
3. Se as regras nº 1 e 2 forem falsas, podemos comparar o valor do nó atual e o valor dado se forem iguais. Se a comparação retornar True, podemos dizer: "Sim! Nossa árvore tem o valor dado", caso contrário, dizemos: "Não, não tem".

Agora, vamos transformar isso em código.

class BinarySearchTree:
    def __init__(self, value):
        self.value = value
        self.left_child = None
        self.right_child = None

    def find_node(self, value):
        if value < self.value and self.left_child:
            return self.left_child.find_node(value)
        if value > self.value and self.right_child:
            return self.right_child.find_node(value)

        return value == self.value

Vamos detalhar o código:

• As linhas 8 e 9 estão sob a regra nº 1.
• As linhas 10 e 11 estão sob a regra nº 2.
• A linha 13 está sob a regra nº 3.

Como testamos isso?

Vamos criar a nossa árvore binária de busca, inicializando o nó raiz com o valor 15.

bst = BinarySearchTree(15)

Agora, vamos inserir muitos nós novos.

bst.insert_node(10)
bst.insert_node(8)
bst.insert_node(12)
bst.insert_node(20)
bst.insert_node(17)
bst.insert_node(25)
bst.insert_node(19)

Para cada nó inserido, testaremos se o nosso método find_node realmente funciona.

print(bst.find_node(15)) # True
print(bst.find_node(10)) # True
print(bst.find_node(8)) # True
print(bst.find_node(12)) # True
print(bst.find_node(20)) # True
print(bst.find_node(17)) # True
print(bst.find_node(25)) # True
print(bst.find_node(19)) # True

Sim, ele funciona para esses valores dados! Vamos testar para um valor que não existe em nossa árvore de busca binária.

print(bst.find_node(0)) # False

Sim. Nossa busca está feita.

Eliminação: remoção e organização

A eliminação é um algoritmo mais complexo porque precisamos tratar de casos diferentes. Para um determinado valor, precisamos remover o nó com este valor. Imagine os seguintes cenários para este nó: ele não tem filhos, tem um único filho ou tem dois filhos.

• Cenário nº 1: um nó sem filhos (nó folha).

#        |50|                              |50|
#      /      \                           /    \
#    |30|     |70|   (DELETE 20) --->   |30|   |70|
#   /    \                                \
# |20|   |40|                             |40|

Se o nó que queremos excluir não tem filhos, simplesmente o excluímos. O algoritmo não precisa reorganizar a árvore.

• Cenário nº 2: um nó com apenas um filho (filho da esquerda ou filho da direita).

#        |50|                              |50|
#      /      \                           /    \
#    |30|     |70|   (DELETE 30) --->   |20|   |70|
#   /            
# |20|

Neste caso, nosso algoritmo precisa fazer com que o pai do nó aponte para o nó filho. Se o nó for o filho da esquerda, fazemos com que o pai do filho da esquerda aponte para o filho. Se o nó for o filho da direita do seu pai, fazemos com que o pai do filho da direita aponte para o filho.

• Cenário nº 3: uim nó com dois filhos.

#        |50|                              |50|
#      /      \                           /    \
#    |30|     |70|   (DELETE 30) --->   |40|   |70|
#   /    \                             /
# |20|   |40|                        |20|

Quando o nó tem dois filhos, precisamos encontrar o nó com o valor mínimo, a começar pelo filho da direita do nó. Colocaremos este nó com o valor mínimo no lugar do nó que queremos remover.

É hora de transformar isso em código.

def remove_node(self, value, parent):
    if value < self.value and self.left_child:
        return self.left_child.remove_node(value, self)
    elif value < self.value:
        return False
    elif value > self.value and self.right_child:
        return self.right_child.remove_node(value, self)
    elif value > self.value:
        return False
    else:
        if self.left_child is None and self.right_child is None and self == parent.left_child:
            parent.left_child = None
            self.clear_node()
        elif self.left_child is None and self.right_child is None and self == parent.right_child:
            parent.right_child = None
            self.clear_node()
        elif self.left_child and self.right_child is None and self == parent.left_child:
            parent.left_child = self.left_child
            self.clear_node()
        elif self.left_child and self.right_child is None and self == parent.right_child:
            parent.right_child = self.left_child
            self.clear_node()
        elif self.right_child and self.left_child is None and self == parent.left_child:
            parent.left_child = self.right_child
            self.clear_node()
        elif self.right_child and self.left_child is None and self == parent.right_child:
            parent.right_child = self.right_child
            self.clear_node()
        else:
            self.value = self.right_child.find_minimum_value()
            self.right_child.remove_node(self.value, self)

        return True

1. Primeiro: observe o valor dos parâmetros e o pai. Queremos encontrar o nó que tem este valor. O nó pai é importante para a remoção do nó.
2. Segundo: observe o valor de retorno. Nosso algoritmo retornará um valor booleano. Ele retorna True se encontrar o nó e o remove. Caso contrário, ele retornará False
3. Da linha 2 à linha 9: começamos a procurar o nó que tem o valor que estamos procurando. Se o valor for menor que o valor atual, vamos para a subárvore da esquerda, recursivamente (se, e somente se, o nó atual tiver um filho da esquerda). Se o valor for maior, vamos para a subárvore da direita, recursivamente.
4. Linha 10: começamos a pensar sobre o algoritmo de remoção.
5. Da linha 11 à linha 13: cobrimos o nó sem filhos. É o filho da esquerda do seu pai. Removemos o nó definindo o filho da esquerda do pai como None.
6. Linhas 14 e 15: cobrimos o nó sem filhos. É o filho da direita do seu pai. Removeremos o nó definindo o filho da direita do pai como None.
7. Método de limpeza do nó: mostrarei o código de clear_node abaixo. Ele define os nós do filho da esquerda, do filho da direita e o valor do nó para None.
8. Da linha 16 à linha 18: cobrimos o nó com apenas um filho (filho da esquerda). É o filho da esquerda do seu pai. Ajustamos o filho da esquerda do pai para o filho da esquerda do nó (o único filho que ele tem).
9. Da linha 19 à linha 21: cobrimos o nó com apenas um filho (filho da esquerda), e ele é o filho da direita do seu pai. Configuramos o filho da direita do pai para o filho da esquerda do nó (o único filho que ele tem).
10. Da linha 22 à linha 24: cobrimos o nó com apenas um filho (filho da direita), e ele é o filho da esquerda do seu pai. Configuramos o filho da esquerda do pai para o filho da direita do nó (o único filho que ele tem).
11. Da linha 25 à linha 27: cobrimos o nó com apenas um filho (filho da direita), e ele é o filho da direita do seu pai. Colocamos o filho da direita do pai no filho da direita do nó (o único filho que ele tem).
12. Da linha 28 à linha 30: cobrimos o nó com o filho da esquerda e o filho da direita. Obtemos o nó com o menor valor (o código é mostrado abaixo) e o configuramos com o valor do nó atual. Termine removendo o menor nó.
13. Linha 32: se encontrarmos o nó que estamos procurando, ele precisa retornar True. Da linha 11 à linha 31, tratamos desse caso. Então, basta retornar True e pronto.

• Para usar o método clear_node: configure o valor None para todos os três atributos — (value, left_child e right_child)

def clear_node(self):
    self.value = None
    self.left_child = None
    self.right_child = None

• Para usar o método find_minimum_value: desça para a esquerda. Se não conseguirmos encontrar mais nós, encontramos o menor.

def find_minimum_value(self):
    if self.left_child:
        return self.left_child.find_minimum_value()
    else:
        return self.value

Agora vamos testá-lo.

Usaremos esta árvore para testar nosso algoritmo remove_node.

#        |15|
#      /      \
#    |10|     |20|
#   /    \    /    \
# |8|   |12| |17| |25|
#              \
#              |19|

Vamos remover o nó com o valor 8. É um nó sem filho.

print(bst.remove_node(8, None)) # True
bst.pre_order_traversal()

#     |15|
#   /      \
# |10|     |20|
#    \    /    \
#   |12| |17| |25|
#          \
#          |19|

Agora, vamos remover o nó com o valor 17. É um nó com apenas um filho.

print(bst.remove_node(17, None)) # True
bst.pre_order_traversal()

#        |15|
#      /      \
#    |10|     |20|
#       \    /    \
#      |12| |19| |25|

Finalmente, removeremos um nó com dois filhos. Esta é a raiz da nossa árvore.

print(bst.remove_node(15, None)) # True
bst.pre_order_traversal()

#        |19|
#      /      \
#    |10|     |20|
#        \        \
#        |12|     |25|

Os testes agora estão prontos. :)

Isso é tudo por enquanto!

Parabéns por terminar este conteúdo denso. É realmente difícil entender um conceito que não conhecemos, mas você conseguiu. :)

Este é mais um passo adiante na minha jornada de aprendizagem e domínio de algoritmos e estruturas de dados. Você pode ver a documentação de minha jornada completa aqui na minha publicação Renaissance Developer (em inglês).

Divirta-se, continue aprendendo e programando.

Twitter e Github do autor. ☺

Recursos adicionais (em inglês)

• Introdução à estrutura de dados em árvore, da mycodeschool
• Como não ser atropelado pelas árvores, do talentoso Vaidehi Joshi
• Introdução às árvores, palestra do professor Jonathan Cohen
• Introdução às árvores, palestra do professor David Schmidt
• Introdução às árvores, palestra do professor Victor Adamchik
• Árvores com Gayle Laakmann McDowell
• Implementação de árvores binárias e testes, por TK
• Curso do Coursera: Estruturas de dados, da Universidade da Califórnia, San Diego
• Curso do Coursera: Estruturas de Dados e desempenho, da Universidade da Califórnia, San Diego
• Conceitos e implementação da árvore binária de busca, de Paul Programming
• Implementação da árvore binária de busca e testes, por TK
• Algoritmo de remoção de nó da árvore binária de busca, de GeeksforGeeks
• Algoritmo de remoção de nó da árvore binária de busca, de Algolist
• Aprendendo Python do zero ao herói
• Travessia de árvores, da Wikipédia

Recursos adicionais (em português)

• Árvore, da Wikipedia