Artigo original: https://www.freecodecamp.org/news/machine-learning-mean-squared-error-regression-line-c7dde9a26b93/
Escrito por: Moshe Binieli
Introdução
Este artigo tratará do método estatístico do erro quadrático médio. Nele, descreverei a relação deste método com a linha de regressão.
O exemplo consiste em pontos sobre o eixo cartesiano. Vamos definir uma função matemática que nos dará a linha reta que melhor passa entre todos os pontos do eixo cartesiano.
Desse modo, aprenderemos a conexão entre esses dois métodos e qual a aparência do resultado de sua conexão.
Explicação geral
Esta é a definição da Wikipédia:
Em estatística, o erro quadrático médio (MSE - Mean Squared Error) de um estimador (de um procedimento para estimar uma quantidade não observada) mede a média dos quadrados dos erros - ou seja, a diferença quadrática média entre os valores estimados e o que é estimado. O MSE é uma função de risco, correspondendo ao valor esperado da perda do erro quadrático. O fato do MSE ser quase sempre estritamente positivo (e diferente de zero) é devido à aleatoriedade ou porque o estimador não dá conta das informações que poderiam produzir uma estimativa mais precisa.
A estrutura do artigo
- Saiba qual é a ideia, veja a visualização gráfica e conheça a equação do erro quadrático médio.
- A parte matemática contém as manipulações algébricas e uma derivada de duas funções variáveis para encontrar um mínimo. Esta seção é para aqueles que querem entender como obtemos as fórmulas matemáticas mais tarde. Você pode ignorá-la se isso não for do seu interesse.
- Uma explicação das fórmulas matemáticas que recebemos e o papel de cada variável na fórmula.
- Exemplos
Saiba qual é a ideia
Digamos que temos sete pontos e que nosso objetivo é encontrar uma linha que minimize as distâncias quadráticas para esses pontos diferentes.
Vamos tentar entender isso.
Vou pegar um exemplo e desenharei uma linha entre os pontos. É claro que meu desenho não é o melhor, mas é apenas para fins de demonstração.
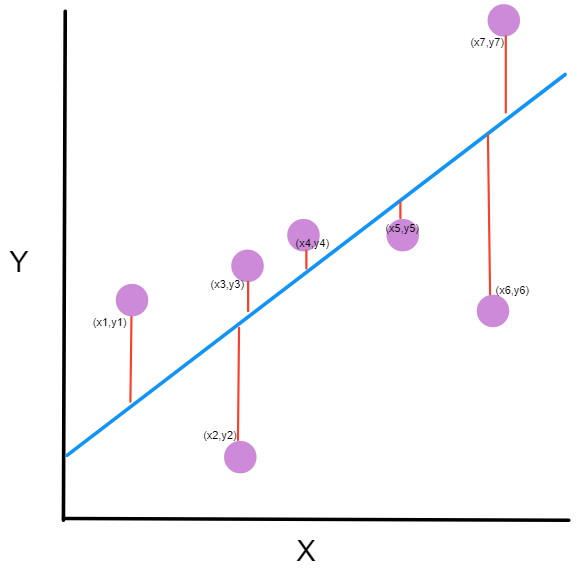
Você pode estar se perguntando: o que é esse gráfico?
- os pontos roxos são os pontos do gráfico. Cada ponto tem uma coordenada x e uma coordenada y.
- A linha azul é a nossa linha de previsão. Essa é uma linha que passa por todos os pontos e os ajusta da melhor maneira possível. Essa linha contém os pontos previstos.
- A linha vermelha entre cada ponto roxo e a linha de previsão são os erros. Cada erro é a distância entre o ponto e o seu ponto previsto.
Você deve se lembrar dessa equação de seus dias de escola, y=Mx+B, onde M é a declive da linha e B é o ponto em que a linha intercepta o eixo y (texto em inglês).
Queremos encontrar M (o declive) e B (o ponto de interceptação de y) que minimizam o erro quadrático!
Vamos definir uma equação matemática que nos dará o erro quadrático médio para todos os nossos pontos.
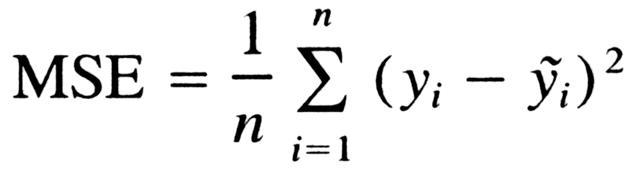
Vamos analisar o que essa equação realmente significa.
- Em matemática, o personagem que parece um E estranho (o sigma, em grego) é chamado de somatório. É a soma de uma sequência de números, de i=1 até i=n. Vamos imaginar isso como um array de pontos, onde passamos por todos os pontos, do primeiro (i=1) ao último (i=n).
- Para cada ponto, tomamos a coordenada y do ponto e a coordenada y' do ponto. A coordenada y é o nosso ponto roxo. O ponto y' está na linha que nós criamos. Subtraímos o valor da coordenada y do valor da coordenada y' e calculamos o quadrado do resultado.
- A terceira parte é pegar a soma de todos os valores (y-y')² e dividi-la por n, o que dará a média.
Nosso objetivo é minimizar esta média, o que nos proporcionará a melhor linha que passa por todos os pontos.
Do conceito às equações matemáticas
Esta parte é para as pessoas que querem entender como chegamos às equações matemáticas. Você pode pular para a próxima parte, se quiser.
Como você sabe, a equação da linha é y=mx+b, onde m é o declive e b é o ponto onde a linha intercepta o eixo y (texto em inglês).
Vamos pegar cada ponto no gráfico e faremos no cálculo de (y-y')². O que é, no entanto, y', e como nós o calculamos? Não temos esse valor como parte dos dados.
Sabemos, contudo, que, para calcular y', precisamos usar nossa equação de linha, y=mx+b, e colocar o x na equação.
A partir daqui, obtemos a seguinte equação:
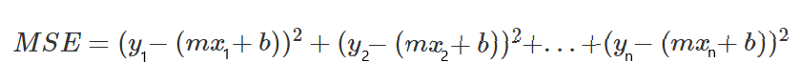
Vamos reescrever esta expressão para simplificá-la.
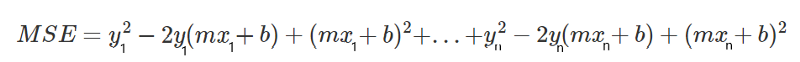
Vamos começar abrindo todos os parênteses da equação. Eu colori a diferença entre as equações para facilitar a compreensão.
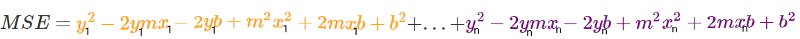
Agora, vamos aplicar outra manipulação. Pegaremos cada parte e a colocaremos em conjunto. Pegaremos todos os y, (-2ymx) e assim por diante e os colocaremos todos lado a lado.
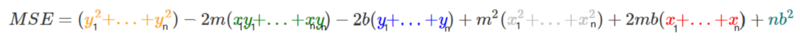
Nesse ponto, estamos começando a ficar confusos. Então, vamos pegar a média de todos os valores quadrados para y, xy, x, x².
Vamos definir, para cada um desses valores, um novo personagem que representará a média de todos os valores quadráticos.
Vejamos um exemplo, vamos pegar todos os valores y e dividi-los por n, já que é a média, e chamar esse valor de de y(ao quadrado e com a linha sobrescrita).
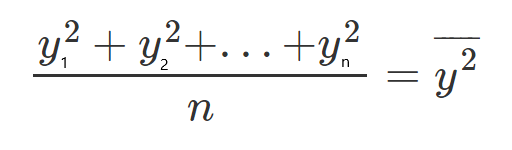
Se multiplicarmos ambos os lados da equação por n, obtemos:
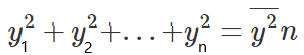
O que nos levará à seguinte equação:
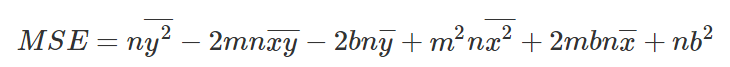
Se olharmos para o que temos, podemos ver que temos uma superfície 3D. Parece um vidro, que se eleva acentuadamente para cima.
Queremos encontrar M e B que minimizem a função. Faremos uma derivada parcial com respeito à M e uma derivada parcial com respeito à B.
Como estamos procurando um ponto mínimo, pegaremos as derivadas parciais e compararemos com 0.
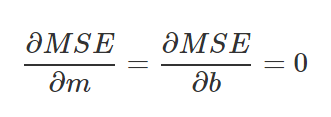
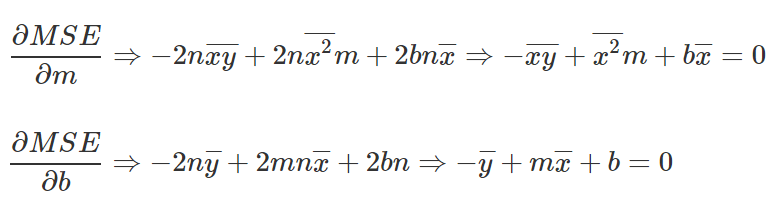
Vamos pegar as duas equações que recebemos, isolando a variável b de ambas, e depois subtraindo a equação superior da equação inferior.
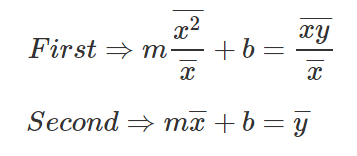
Vamos subtrair a primeira equação da segunda equação
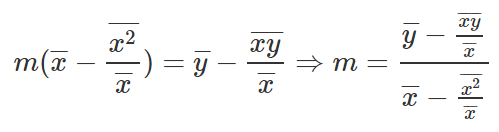
Vamos nos livrar dos denominadores da equação.
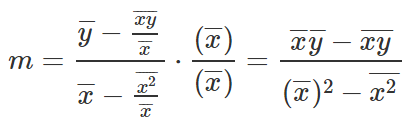
Pronto. Esta é a equação para encontrar M. Vamos pegar isso e escrever a equação B.
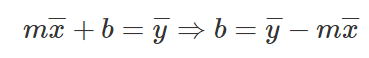
Equações para declive e interceptação de y
Vamos fornecer as equações matemáticas que nos ajudarão a encontrar o declive e a interceptação em y (texto em inglês) necessários.
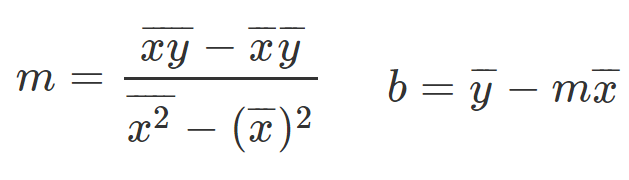
Você, provavelmente, deve estar pensando: que raios são essas equações estranhas?
Elas são realmente simples de entender. Vamos falar um pouco sobre elas.
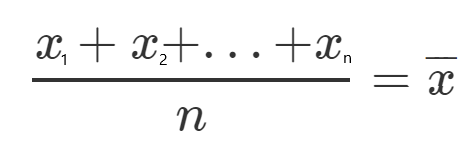
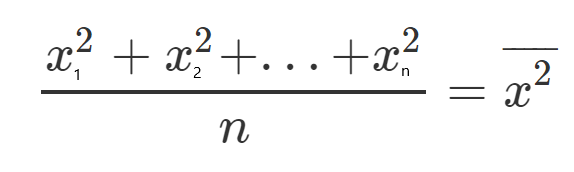
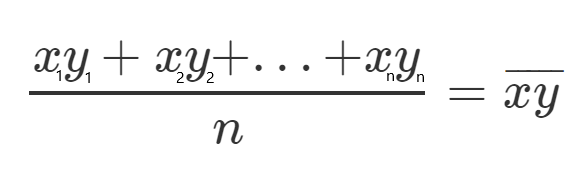
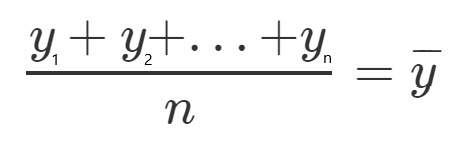
Agora que entendemos nossas equações, é hora de juntar tudo e mostrar alguns exemplos.
Exemplos
Um grande agradecimento à Khan Academy pelos exemplos.
Exemplo nº 1
Vamos pegar 3 pontos, (1,2), (2,1), (4,3).
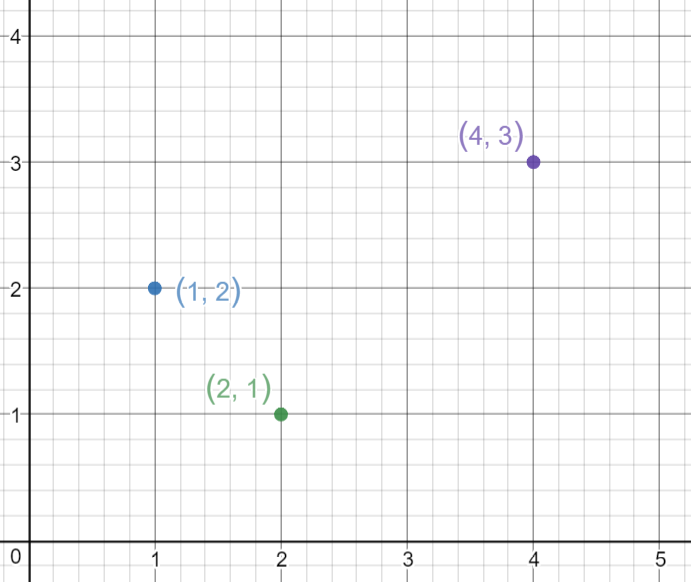
Vamos encontrar M e B para a equação y=mx+b.
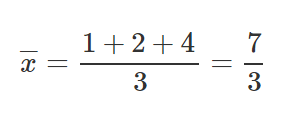
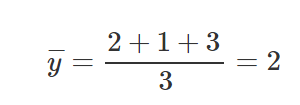
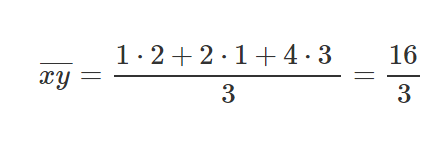
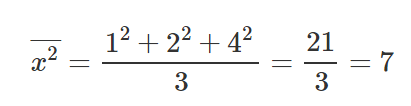
Depois de termos calculado as partes relevantes para nossa equação de M e para a equação de B, vamos colocar esses valores dentro das equações e obter o declive e o ponto de interceptação do eixo y (texto em inglês).
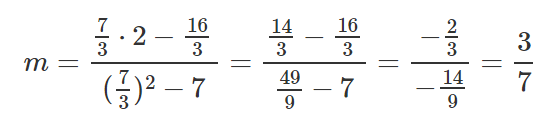
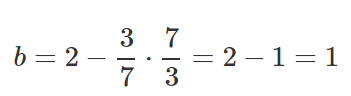
Vamos pegar esses resultados e colocá-los dentro da equação da linha y=mx+b.
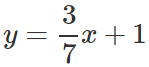
Agora, vamos desenhar a linha e ver como ela passa através das linhas de tal forma que minimize as distâncias quadráticas.
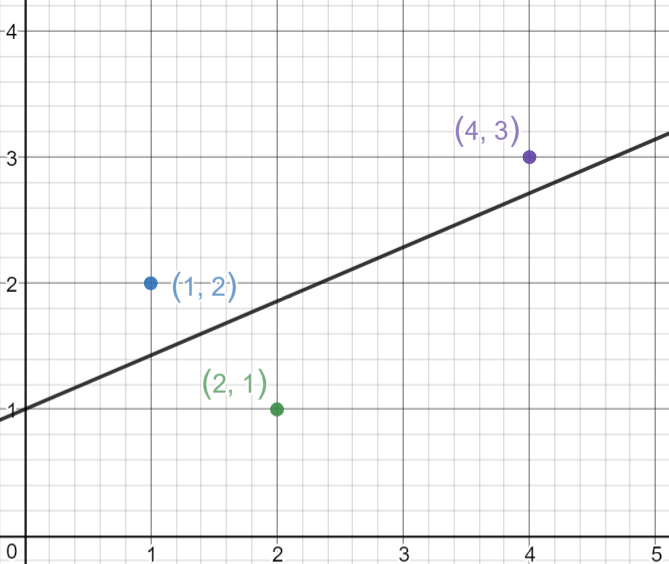
Exemplo nº 2
Vamos pegar 4 pontos, (-2,-3), (-1,-1), (1,2), (4,3).
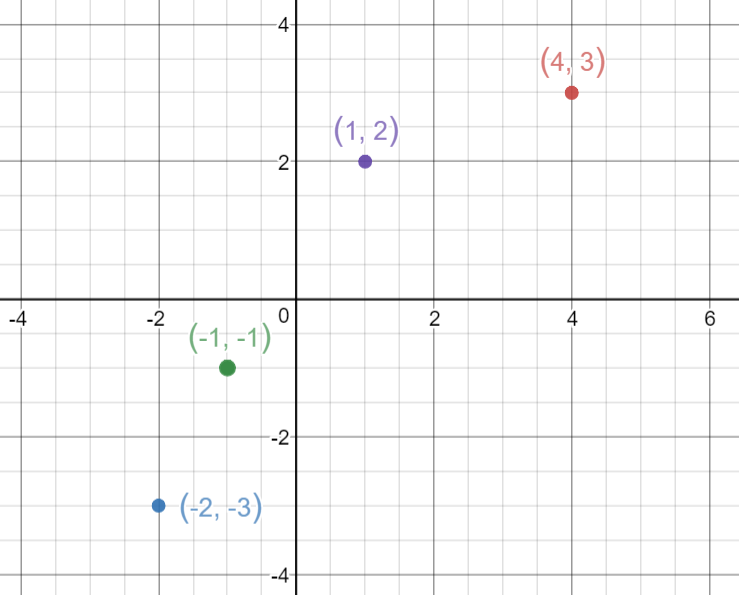
Vamos encontrar M e B para a equação y=mx+b.
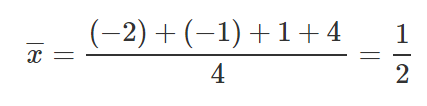
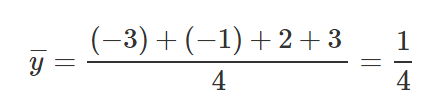
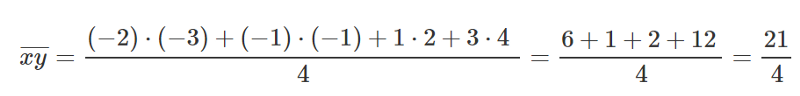
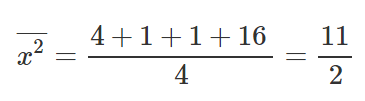
Fazemos o mesmo que fizemos antes. Vamos colocar esses valores dentro das nossas equações para encontrar M e B.
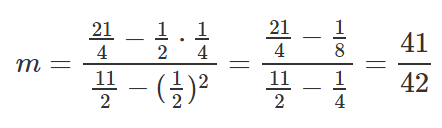
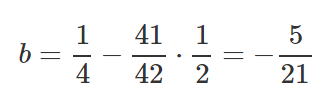
Vamos pegar esses resultados e colocá-los dentro da equação da linha y=mx+b.
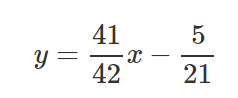
Agora, vamos desenhar a linha e ver como a linha passa através das linhas de tal forma que minimize as distâncias quadráticas.
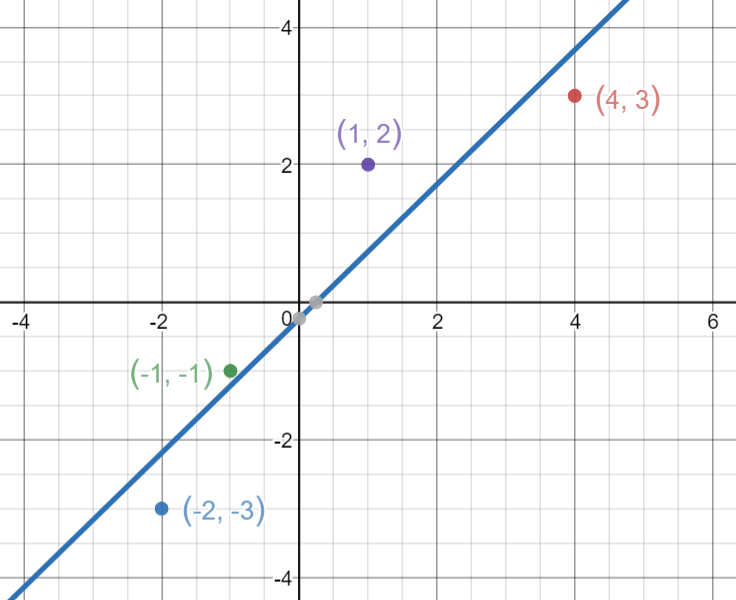
Em conclusão
Como você pode ver, toda a ideia é simples. Precisamos apenas entender as partes principais e como trabalhamos com elas.
Você pode trabalhar com as fórmulas para encontrar a linha em outro gráfico e fazer um cálculo simples e obter os resultados para o declive e o ponto de interceptação de y (texto em inglês).
Isso é tudo. Simples, não?
Todo comentário e todo feedback é bem-vindo – se for necessário, o autor ajustará o artigo. Fique à vontade para entrar em contato diretamente com o autor pelo LinkedIn.

