Artigo original: https://www.freecodecamp.org/news/recursion-is-not-hard-858a48830d83/
Escrito por: Kevin Turney
Já vou dizendo isso de cara: você sabe os eventos que acontecem quando uma função é invocada? Não? Então, começaremos daqui.
Chamando uma função
Quando nós chamamos uma função, um contexto de execução ocorre na pilha de execução. Vamos entrar em detalhes mais específicos abaixo.
Primeiro, o que é uma pilha?
Uma pilha é uma estrutura de dados que opera com base em "o último a entrar é o primeiro a sair". Um item é "colocado" (em inglês, pushed) em uma pilha quando o estamos adicionando e é "retirado" (em inglês, popped) da pilha quando queremos removê-lo.
Usar uma pilha é um método de ordenar um determinado número de operações para a execução.
Agora, o que seria um contexto de execução? Um contexto de execução é criado quando temos uma chamada de função. Esse contexto ocorre em uma pilha de execução, uma ordem de operações. O item que é sempre o primeiro nessa pilha é o contexto de execução global. Logo após, estão os contextos criados pelas funções.
Esses contextos de execução tem propriedades, um objeto de ativação e um "this" vinculado. O "this" vinculado é uma referência de volta ao contexto de execução. O objeto de ativação inclui: parâmetros passados, declaração de variáveis e declaração de funções.
Então, toda vez que colocamos um novo contexto na pilha, normalmente, temos tudo de que precisamos para executar o código.
Por que eu disse normalmente?
Com recursão, estamos esperando retornar valores vindo de outros contextos de execução. Esses outros contextos de execução estão em pontos mais altos na pilha. Quando o último item na pilha finaliza a execução, esse contexto gerado retorna um valor. Esse valor retornado é passado como um valor retornado pelo caso recursivo para o próximo item. O contexto de execução, então, é retirado da pilha.
Recursão
Então, o que é recursão?
Uma função recursiva é uma função que chama a si mesma até que a "condição base" seja verdadeira e a execução pare.
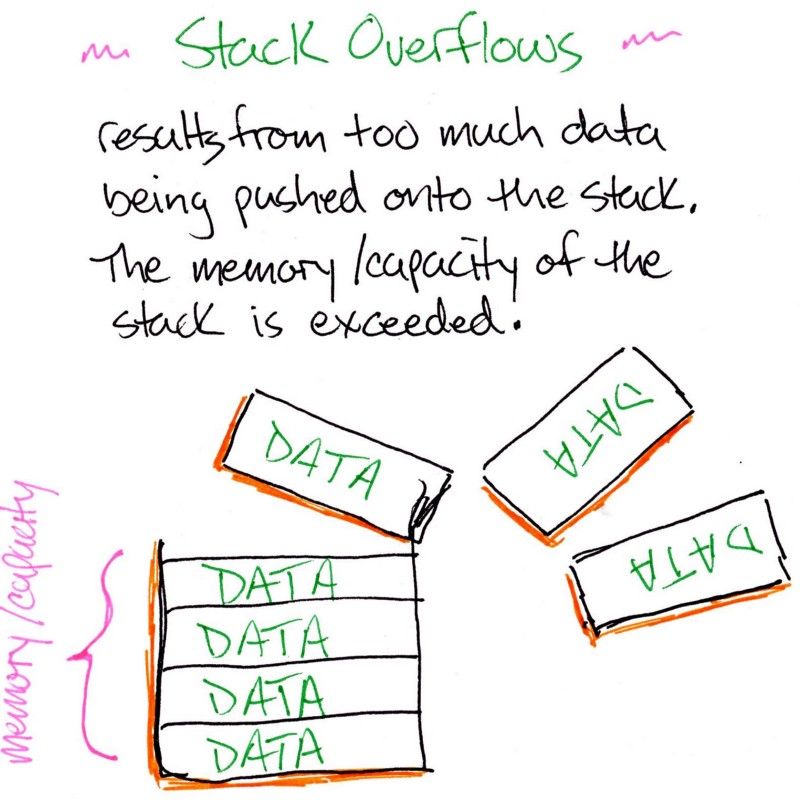
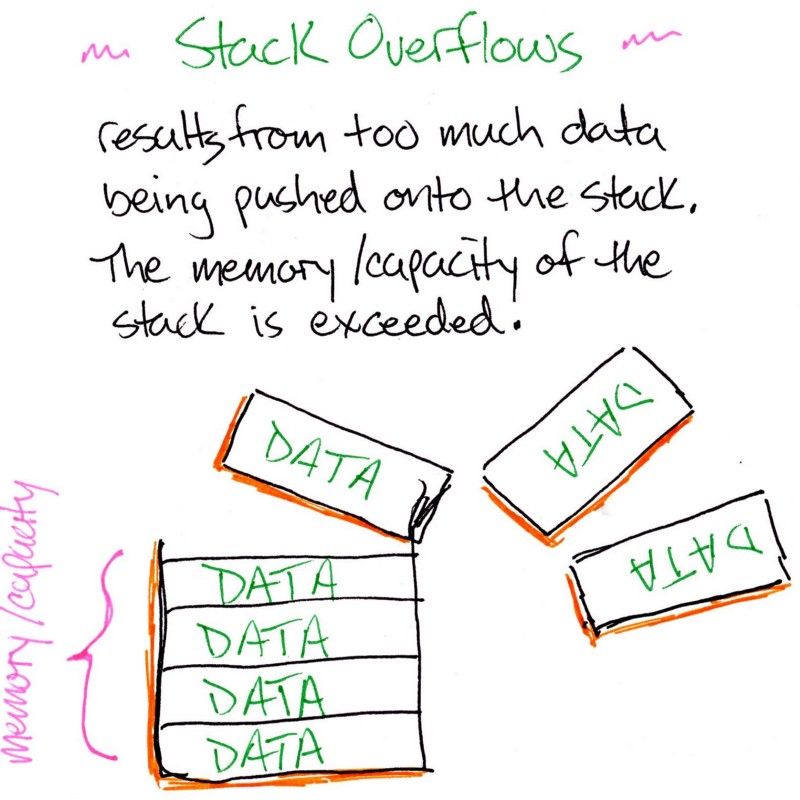
Enquanto for falsa, continuaremos colocando o contexto de execução em cima da pilha. Isso pode acontecer até que tenhamos um sobrefluxo da pilha – ou, em inglês, "stack overflow". Um stack overflow ocorre quando ficamos sem memória para manter os itens na pilha.
Em geral, uma função recursiva tem ao menos duas partes: uma condição base e, ao menos, um caso recursivo.
Vamos olhar um exemplo clássico.
Fatorial
const fatorial = function(num) {
debugger;
if (num === 0 || num === 1) {
return 1
} else {
return num * fatorial(num - 1)
}
}fatorial(5)Aqui, estamos tentando encontrar 5! (o fatorial de cinco). A função fatorial (texto em inglês) é definida como o produto de todos os números positivos menores ou iguais ao seu argumento.
A primeira condição é: "se o parâmetro passado for igual a 0 ou 1, terminaremos a chamada e retornaremos 1".
Para os casos recursivos, faremos o seguinte:
"Se o parâmetro não for 0 ou 1, passaremos o valor de num vezes o valor de retorno da função chamada outra vez com o argumento de num-1".
Então, se chamarmos fatorial(0), a função retornará 1 e nunca atingirá o caso recursivo.
A mesma situação ocorre com fatorial(1).
Podemos ver o que está acontecendo se inserirmos uma instrução debugger dentro do código e se usarmos as ferramentas do desenvolvedor para segui-lo e observar a chamada da pilha (em inglês, stack).
- A stack de execução coloca o 5 como argumento dentro da função
fatorial(). O caso base é falso, entrando na condição recursiva. - A stack de execução então chama a função
fatorial()uma segunda vez com o argumentonum-1(4) como argumento. O caso base é falso entrando, assim, na condição recursiva. - A stack de execução chamará
fatorial()uma terceira vez com o argumentonum-1(3). O caso base é falso. Portanto, outra vez, entramos na condição recursiva. - A stack de execução chama
fatorial()uma quarta vez comnum-1(2) como seu argumento. O caso base é falso. Entramos na condição recursiva. - A stack executa
fatorial()uma quinta vez comnum-1(1) como seu argumento. Aqui o caso base é verdadeiro. Então, retornamos 1.
Nesse ponto, diminuímos o argumento passado por 1 em cada chamada de função, até alcançarmos a condição de retorno 1.
6. A partir daí, o último contexto de execução completa num === 1. Então, a função retorna 1.
7. A seguir, temos num === 2. O valor retornado é 2. (1×2).
8. Depois, temos num === 3. Retornamos 6. (2×3). Até agora, temos 1×2×3.
9. Posteriormente, temos num === 4, (4×6). 24 é o valor retornado no próximo contexto.
10. Finalmente, num === 5, (5×24) e, aqui, teremos 120 como valor final.

Recursão é bem elegante, certo?
Poderíamos ter feito a mesma coisa com um laço for ou while, mas, usando recursão, temos uma alternativa mais apresentável e bonita.
É por isso que usamos soluções recursivas.
Muitas vezes, um problema dissecado em partes menores é mais eficiente e ajuda a superá-lo mais facilmente. Desse modo, recursão é uma abordagem do tipo dividir-e-conquistar para resolver obstáculos.
- Subproblemas são mais fáceis de solucionar que o problema original;
- Soluções para subproblemas são combinadas para resolver o problema original.
"Dividir-e-conquistar" é bastante utilizado para atravessar ou buscar em estrutura de dados como em árvores de busca binária, gráficos e pilhas. Isso também funciona com muitos algoritmos de ordenação, como quicksort e heapsort (links em inglês).
Vamos trabalhar com alguns exemplos. Usaremos as ferramentas do desenvolvedor para ter um entendimento conceitual do que está acontecendo, onde e quando. Vamos lembrar de usar a ferramenta debugger e seguir passo a passo cada parte do processo.
Fibonacci
const fibonacci = function(num) {
if (num <= 1) {
return num
} else {
return fibonacci(num - 1) + fibonacci(num - 2)
}
}
fibonacci(5);Arrays recursivos
function aplainar(arr) {
var result = [] arr.forEach(function(element) {
if (!Array.isArray(element)) {
result.push(element)
} else {
result = result.concat(aplainar(element))
}
})
return result
}
aplainar([1, [2], [3, [[4]]]]);Invertendo uma string
function inverter(str) {
if (str.length === 0) return ''
return str[str.length - 1] + inverter(str.substr(0, str.length - 1))
}
inverter('abcdefg');Quicksort
function quickSort(arr, lo, hi) {
if (lo === undefined) lo = 0
if (hi === undefined) hi = arr.length - 1
if (lo < hi) { // fazer o particionamento do array
var p = partition(arr, lo, hi)
console.log('partição de, ' + lo + ' até ' + hi + '=> partition: ' + p) // ordenar os subarrays
quickSort(arr, lo, p - 1)
quickSort(arr, p + 1, hi)
} // para a chamada inicial, retornar um array ordenado
if (hi - lo === arr.length - 1) return arr
}
function partition(arr, lo, hi) {
// seleciona o último elemento como pivot
var pivot = arr[hi]
// rastreia o index onde colocar o pivot
var pivotLocation = lo
// percorre o subarray e se element <= pivot, coloca element antes do pivot
for (var i = lo; i < hi; i++) {
if (arr[i] <= pivot) {
swap(arr, pivotLocation, i)
pivotLocation++
}
}
swap(arr, pivotLocation, hi)
return pivotLocation
}
function swap(arr, index1, index2) {
if (index1 === index2) return
var temp = arr[index1]
arr[index1] = arr[index2]
arr[index2] = temp
console.log('trocados' + arr[index1], arr[index2], +' em ', arr)
return arr
}
quickSort([1, 4, 3, 56, 9, 8, 7, 5])Praticar técnicas de recursão é importante. Para estruturas de dados aninhadas como árvores, gráficos e pilhas, a recursão é inestimável.
Em um artigo futuro, discutirei otimização das chamada da cauda (em inglês, tail-call), técnicas de memoização e como elas se relacionam à recursão.
Agradeço por ter me acompanhado até aqui!
Recursos complementares
Software Engineering (em inglês)
Outro artigo interessante (em inglês)
Material de curso aberto (gratuito) da M.I.T. (em inglês)