Artigo original: If you have slow loops in Python, you can fix it…until you can’t
Escrito por: Maxim Mamaev
Vamos pegar um problema computacional como exemplo, escrever o código e ver como podemos melhorar o tempo de execução. Aqui vamos nós.
Montando a cena: o problema da mochila
Este é o problema computacional que usaremos como exemplo:
O problema da mochila é um problema bem conhecido em otimização combinatória. Nesta seção, revisaremos seu tipo mais comum, o problema da mochila 0–1, e sua solução por meio de programação dinâmica. Se você estiver familiarizado com o assunto, pode pular essa parte.
Você recebe uma mochila de capacidade C e uma coleção de N itens. Cada item tem peso w[i] e valor v[i]. Sua tarefa é arrumar a mochila com os itens mais valiosos. Em outras palavras, você deve maximizar o valor total dos itens que coloca na mochila, com uma restrição: o peso total dos itens levados não pode exceder a capacidade da mochila.
Depois de obter uma solução, o peso total dos itens na mochila é chamado de "peso da solução" e seu valor total é o "valor da solução".
O problema tem muitas aplicações práticas. Por exemplo, você decidiu investir R$ 1.600 em uma famosa ação da FAANG (nome coletivo das ações do Facebook, Amazon, Apple, Netflix e Google, também conhecida como Alphabet). Cada ação tem um preço de mercado atual e a estimativa de preço de um ano. A partir de um dia em 2018, eles são os seguintes:
========= ======= ======= ==========
Empresa Ticker Preço Estimativa
========= ======= ======= ==========
Alphabet GOOG 1030 1330
Amazon AMZN 1573 1675
Apple AAPL 162 193
Facebook FB 174 216
Netflix NFLX 312 327
========= ======= ======= ==========Para simplificar o exemplo, vamos supor que você nunca colocaria todos os seus ovos na mesma cesta. Você está disposto(a) a comprar não mais do que uma ação de cada. Quais ações você compra para maximizar seu lucro?
Esse é um problema da mochila. Seu orçamento (R$ 1.600) é a capacidade (C) de armazenamento. As ações são os itens a serem embalados. Os preços atuais são os pesos (w). As estimativas de preços são os valores. O problema parece trivial. No entanto, a solução não é evidente à primeira vista – se você deve comprar uma ação da Amazon, ou uma ação do Google mais uma de alguma combinação de Apple, Facebook, ou Netflix.
Claro que, nesse caso, você pode fazer cálculos rápidos à mão e chegar na solução: você deve comprar Google, Netflix, e Facebook. Desse modo, você gasta R$ 1.516 e espera ganhar R$ 1.873.
Agora, você acredita que descobriu uma mina de outro. Você destrói seu cofrinho e recebe R$ 10.000. Apesar de sua empolgação, você permanece inflexível com a regra "uma ação – uma compra". Portanto, com esse orçamento maior, você tem que ampliar suas opções. Você decide considerar todas as 100 ações da lista da NASDAQ como candidatas para compra.
O futuro nunca foi tão brilhante, mas, de repente, você percebe que, para identificar sua carteira de investimentos ideal, você terá que verificar cerca de 2¹⁰⁰ combinações. Mesmo que você seja superotimista com a iminência e a onipresença da economia digital, qualquer economia requer — no mínimo — um universo onde funcione. Infelizmente, em alguns trilhões de anos, quando sua computação terminar, nosso universo provavelmente não existirá.
Algoritmo de programação dinâmica
Temos que abandonar a abordagem de força bruta e programar alguma solução inteligente. Pequenos problemas de mochila (e o nosso é pequeno, acredite ou não) são resolvidos por programação dinâmica. A ideia básica é partir de um problema trivial cuja solução conhecemos e depois adicionaremos complexidade passo a passo.
Se você achar as explicações a seguir muito abstratas, aqui está uma ilustração comentada da solução para um problema de mochila bem pequeno. Isso ajudará você a visualizar o que está acontecendo.
Suponha que, dados os primeiros itens i da coleção, nós saibamos os valores de solução s(i, k) para todas as capacidades de mochila k no intervalo de 0 a C.
Em outras palavras, costuramos mochilas "auxiliares" C+1 de todos os tamanhos de 0 a C. Em seguida, organizamos nossa coleção, pegamos o primeiro item i e temporariamente separamos todo o resto. E agora assumimos que, por alguma mágica, nós sabemos como embalar de maneira ideal cada um dos pacotes desse conjunto funcional de i itens. Os itens que escolhemos do conjunto funcional podem ser diferentes para pacotes diferentes, mas no momento não estamos interessados em quais itens pegamos ou pulamos. É apenas o valor da solução s(i, k) que registramos para cada um de nosso pacotes recém costurados.
Agora, buscamos o próximo item (i+1)º da coleção e adicionamos ao conjunto funcional. Vamos encontrar valores de solução para todas as mochilas auxiliares com esse novo conjunto funcional. Em outras palavras, nós encontramos s(i+1, k) para todo k=0..C dado s(i, k).
Se k for menor que o peso do novo item w[i+1], não podemos pegar esse item. De fato, mesmo que pegássemos apenas esse item, ele sozinho não caberia na mochila. Portanto, s(i+1, k) = s(i, k) para todo k < w[i+1].
Para os valores k >= w[i+1] temos que fazer uma escolha: ou colocamos o novo item na mochila de capacidade k ou o pulamos. Temos que avaliar essas duas opções para determinar qual delas nos dá mais valor embalado no pacote.
Se pegarmos o (i+1)º item, adquirimos o valor v[i+1] e consumimos a parte da capacidade da mochila para acomodar o peso w[i+1]. Isso nos deixa com a capacidade k–w[i+1] que devemos preencher de modo otimizado usando (alguns dos) primeiros i itens. Esse preenchimento otimizado tem o valor de solução s(i, k–w[i+1]). Esse número já é conhecido por nós porque, por suposição, conhecemos todos os valores de solução para o conjunto funcional de i itens. Portanto, o valor da solução candidata para a mochila k com o item i+1 levado seria
s(i+1, k | i+1 levado) = v[i+1] + s(i, k–w[i+1]).
A outra opção seria pular o item i+1. Nesse caso, nada muda em nossa mochila, e o valor da solução candidata seria o mesmo que s(i, k).
Para decidir sobre a melhor opção, comparamos os dois candidatos para os valores da solução:
s(i+1, k | i+1 levado) = v[i+1] + s(i, k–w[i+1])
s(i+1, k | i+1 ignorado) = s(i, k)
O máximo destes torna-se a solução s(i+1, k).
Resumindo:
if k < w[i+1]:
s(i+1, k) = s(i, k)
else:
s(i+1, k) = max( v[i+1] + s(i, k-w[i+1]), s(i, k) )Agora, podemos resolver o problema da mochila passo a passo. Começamos com o conjunto de trabalho vazio (i=0). Obviamente, s(0, k) = 0 para qualquer k. Em seguida, avançamos adicionando itens ao conjunto de trabalho e encontrando os valores de solução s(i, k) até chegarmos a s(i+1=N, k=C), que é o valor de solução do problema original.
Observe que, ao fazer isso, construímos a grade de valores da solução NxC.
No entanto, apesar de ter aprendido o valor da solução, não sabemos exatamente quais itens foram colocados na mochila. Para descobrir isso, retrocedemos a grade. Partindo de s(i=N, k=C), comparamos s(i, k) com s(i–1, k).
Se s(i, k) = s(i–1, k), o i-ésimo item não foi considerado. Nós reiteramos com i=i–1 mantendo o valor de k inalterado. Caso contrário, o i-ésimo item foi retirado e, para a próxima etapa de exame, encolhemos a mochila em w[i] — definimos i=i–1, k=k–w[i].
Desse modo, examinamos todos os itens do N-ésimo ao primeiros e determinamos quais deles foram colocados na mochila. Isso nos dá a solução para o problema da mochila.
Código e análise
Como temos o algoritmo, vamos comparar várias implementações, começando por uma simples. O código está disponível no GitHub.
Os dados são a lista Nasdaq 100, contendo preços atuais e estimativas de preços para cem ações (até um dia em 2018). Nosso orçamento de investimento é de R$ 10.000.
Lembre-se que preços de ações não são números redondos em reais, mas vêm com centavos. Portanto, para obter a solução exata, temos que contar tudo em centavos — definitivamente queremos evitar números float. Portanto, a capacidade de nossa mochila é ($)10.000 x 100 centavos = ($)1.000.000, e o tamanho total de nosso problema N x C = 1.000.000.
Com um inteiro ocupando 4 bytes de memória, esperamos que o algoritmo vá consumir aproximadamente 400 MB de RAM. Portanto, a memória não será uma limitação. É com o tempo de execução que devemos no preocupar.
Claro, todas as nossas implementações produzirão a mesma solução. Para referência, o investimento (o peso da solução) é 999930 (R$ 9.999,30) e o retorno esperado (o valor da solução) é 1219475 (R$ 12.194,75). A lista de ações a comprar é bem longa (80 de 100 itens). Você pode obtê-la rodando o código.
Lembre-se de que este é um exercício de programação, não um conselho de investimento. Quando você for ler esse artigo, os preços e as estimativas terão mudado em relação ao que é usado aqui como exemplo.

Os bons e velhos loops do tipo "for"
A implementação direta do algoritmo é dada abaixo.
def solve_naive(capacity, items, weights, values):
grid = [[0] * (capacity+1)]
for item in range(items):
grid.append(grid[item].copy())
for k in range(weights[item], capacity+1):
grid[item + 1][k] = max(grid[item][k], grid[item][k-weights[item]] + values[item])
solution_value = grid[items][capacity]
solution_weight = 0
taken = []
k = capacity
for item in range(items, 0, -1):
if grid[item][k] != grid[item-1][k]:
taken.append(item - 1)
k -= weights[item - 1]
solution_weight += weights[item-1]
return solution_value, solution_weight, takenExistem duas partes.
Na primeira parte (linhas 3-7 acima), dois loops for aninhados são usados para construir a grade da solução.
O loop externo adiciona itens ao conjunto de trabalho até atingirmos N (o valor de N é passado no parâmetro items). A linha de valores de solução para cada novo conjunto de trabalho é inicializada com os valores calculados para o conjunto de trabalho anterior.
O loop interno para cada conjunto de trabalho itera os valores de k do peso do item recém adicionado a C (o valor de C é passado no parâmetro capacity).
Note que não precisamos iniciar o loop de k=0. Quando k é menor do que o peso do item, os valores da solução são sempre os mesmos calculados para o conjunto de trabalho anterior. Esses números já foram copiados para a linha atual pela inicialização.
Quando os loops são concluídos, temos a grade e o valor da solução.
A segunda parte (linhas 9-17) é um único loop for de N iterações. Ele retrocede a grade para descobrir quais itens foram levados pela mochila.
Mais adiante, nos concentraremos exclusivamente na primeira parte do algoritmo, já que este possui complexidade de tempo e espaço O(N*C). A parte de retrocesso requer apenas tempo O(N) e não gasta nenhuma memória adicional – seu consumo de recursos é relativamente insignificante.
A implementação direta leva 180 segundos para resolver o problema da mochila Nasdaq 100 no meu computador.
Isso é muito ruim? Por um lado, com as velocidades da era moderna, não estamos acostumados a passar três minutos esperando que um computador faça as coisas. Por outro lado, o tamanho do problema - cem milhões - parece realmente intimidador, então, talvez, três minutos seja ok?
Para obter algum benchmark, vamos programar o mesmo algoritmo em outra linguagem. Precisamos de uma linguagem compilada estaticamente tipada para garantir a velocidade de computação. Não, não C. Não é chique. Vamos seguir a moda e escrever em Go:
func solver(capacity, items int, weights, values []int) (int, int, []int) {
grid := make([][]int, items+1, items+1)
grid[0] = make([]int, capacity+1, capacity+1)
for item := 0; item < items; item++ {
grid[item+1] = make([]int, capacity+1, capacity+1)
for k:=0; k<weights[item]; k++ {
grid[item + 1][k] = grid[item][k]
}
for k:=weights[item]; k <= capacity; k++ {
grid[item + 1][k] = max(grid[item][k], grid[item][k-weights[item]] + values[item])
}
}
solution_value := grid[items][capacity]
solution_weight := 0
var taken []int
k := capacity
for item := items; item > 0; item-- {
if grid[item][k] != grid[item-1][k] {
taken = append(taken, item-1)
k -= weights[item - 1]
solution_weight += weights[item-1]
}
}
return solution_value, solution_weight, taken
}Como você pode ver, o código Go é bem similar ao do Python. Até copiei e colei uma linha, a mais longa, como está.
Qual é o tempo de execução? 400 milissegundos! Em outras palavras, o Python foi 500 vezes mais lento do que o Go. A lacuna provavelmente será ainda maior se tentarmos em C. Isso é definitivamente um desastre para o Python.

Para descobrir o que torna o código Python mais lento, vamos executá-lo com o line profiler. Você pode encontrar a saída do profiler para esta implementação e as subsequentes do algoritmo no GitHub.
No solucionador direto, 99,7% do tempo de execução é gasto em duas linhas. Essas duas linhas compõem o loop interno, que é executado 98 milhões de vezes:
Line # Hits Time Per Hit % Time Line Contents
==============================================================
...
42 101 170.0 1.7 0.0 for item in range(items):
43 100 1457275.0 14572.8 0.3 grid.append(grid[item].copy())
44 98387558 121134401.0 1.2 26.4 for k in range(weights[item], capacity+1):
45 98387458 336078747.0 3.4 73.3 grid[item + 1][k] = max(grid[item][k], grid[item][k-weights[item]] + values[item])
...
Peço desculpas pelas linhas excessivamente longas, mas o line profiler não pode lidar adequadamente com quebras de linha na mesma instrução.
Ouvi dizer que o operador for do Python é lento, mas, curiosamente, a maior parte do tempo não é gasta na linha for mas no corpo do loop.
Podemos dividir o corpo do loop em operações individuais para ver se alguma operação específica é muito lenta:
Line # Hits Time Per Hit % Time Line Contents
==============================================================
...
67 101 196.0 1.9 0.0 for item in range(items):
68 100 1454886.0 14548.9 0.2 grid.append(grid[item].copy())
69 100 1463.0 14.6 0.0 wi = weights[item]
70 100 323.0 3.2 0.0 vi = values[item]
71 98387558 133663554.0 1.4 16.7 for k in range(wi, capacity+1):
72 98387458 156110242.0 1.6 19.4 a = grid[item][k]
73 98387458 194935490.0 2.0 24.3 b = grid[item][k-wi] + vi
74 98387458 138902753.0 1.4 17.3 if b > a:
75 60782758 109728042.0 1.8 13.7 grid[item + 1][k] = b
76 else:
77 37604700 67944391.0 1.8 8.5 grid[item + 1][k] = a
...Parece que nenhuma operação em particular se destaca. Os tempos de execução das operações individuais dentro do loop interno são praticamente os mesmos que os tempos de execução de operações análogas em outras partes do código.
Observe como quebrar o código aumentou o tempo total de execução. O loop interno agora leva 99,9% do tempo de execução. Quanto mais burro seu código Python, mais lento ele fica. Interessante, não é?
Função map integrada
Vamos tornar o código mais otimizado e substituir o loop for interno por uma função map() integrada:
def solve_map(capacity, items, weights, values):
grid = [[0] * (capacity+1)]
for item in range(items):
grid.append(grid[item].copy())
this_weight = weights[item]
this_value = values[item]
grid[item+1][this_weight:] =
list(map(lambda k: max(grid[item][k],
grid[item][k - this_weight] + this_value),
range(this_weight, capacity+1)))
solution_value = grid[items][capacity]
solution_weight = 0
taken = []
k = capacity
for item in range(items, 0, -1):
if grid[item][k] != grid[item-1][k]:
taken.append(item - 1)
k -= weights[item - 1]
solution_weight += weights[item-1]
return solution_value, solution_weight, takenO tempo de execução desse código é de 102 segundos, estando 78 segundos abaixo da pontuação da implementação direta. De fato, map() é executado visivelmente, mas não excessivamente, mais rápido.
List comprehension
Você deve ter notado que cada execução do loop interno produz uma lista (que é adicionada à grade de solução como uma nova linha). O jeito do Python de criar listas é, claro, list comprehension. Vamos tentar isso, em vez de map().
def solve_list_comp(capacity, items, weights, values):
grid = [[0] * (capacity+1)]
for item in range(items):
grid.append(grid[item].copy())
this_weight = weights[item]
this_value = values[item]
grid[item+1][this_weight:] =
[max(grid[item][k], grid[item][k - this_weight] + this_value)
for k in range(this_weight, capacity+1)]
solution_value = grid[items][capacity]
solution_weight = 0
taken = []
k = capacity
for item in range(items, 0, -1):
if grid[item][k] != grid[item-1][k]:
taken.append(item - 1)
k -= weights[item - 1]
solution_weight += weights[item-1]
return solution_value, solution_weight, takenO programa terminou em 81 segundos. Conseguimos outra melhoria e reduzimos o tempo de execução pela metade em comparação à implementação direta (180 s). Fora de contexto, isso seria elogiado como um progresso significativo. Infelizmente, ainda estamos a anos-luz do nosso benchmark de 0,4 s.
Arrays do NumPy
Por fim, esgotamos as ferramentas integradas do Python. Sim, posso ouvir o rugido do público cantando "NumPy! NumPy!" Mas, para apreciar a eficiência do NumPy, devemos colocá-lo em contexto, tentando for, map() e list comprehension de antemão.
Ok, agora é a hora do NumPy. Então, abandonamos as listas e colocamos nossos dados em arrays do NumPy:
def solve_list_comp_numpy(capacity, items, weights, values):
grid = np.empty((items + 1, capacity + 1), dtype=int)
grid[0] = 0
for item in range(items):
grid[item+1] = grid[item]
this_weight = weights[item]
this_value = values[item]
grid[item+1, this_weight:] =
[max(grid[item, k], grid[item, k - this_weight] + this_value)
for k in range(this_weight, capacity+1)]
solution_value = grid[items, capacity]
solution_weight = 0
taken = []
k = capacity
for item in range(items, 0, -1):
if grid[item, k] != grid[item-1, k]:
taken.append(item - 1)
k -= weights[item - 1]
solution_weight += weights[item-1]
return solution_value, solution_weight, takenDe repente, o resultado é desencorajador. Este código é executado 1,5 vezes mais devagar do que a solução sem graça por list comprehension (123 s em comparação com os 81 s). Como isso?
Vamos examinar os perfis de linha para ambos solucionadores.
Line # Hits Time Per Hit % Time Line Contents
==============================================================
Vanilla list comprehension
245 1 8212.0 8212.0 0.0 grid = [[0] * (capacity+1)]
246
247 101 1654.0 16.4 0.0 for item in range(items):
248 100 1452204.0 14522.0 0.7 grid.append(grid[item].copy())
249 100 1603.0 16.0 0.0 this_weight = weights[item]
250 100 272.0 2.7 0.0 this_value = values[item]
251
252 100 202696910.0 2026969.1 99.3 grid[item+1][this_weight:] = [max(grid[item][k], grid[item][k - this_weight] + this_value) for k in range(this_weight, capacity+1)]
Using numpy arrays
273 1 42.0 42.0 0.0 grid = np.empty((items + 1, capacity + 1), dtype=int)
274 1 2527.0 2527.0 0.0 grid[0] = 0
275 101 1427.0 14.1 0.0 for item in range(items):
276 100 322952.0 3229.5 0.1 grid[item+1] = grid[item]
277 100 1341.0 13.4 0.0 this_weight = weights[item]
278 100 266.0 2.7 0.0 this_value = values[item]
279 100 311244493.0 3112444.9 99.9 grid[item+1, this_weight:] = [max(grid[item, k], grid[item, k - this_weight] + this_value) for k in range(this_weight, capacity+1)]
A inicialização do grid[0] como um array do NumPy (linha 274) é três vezes mais rápida do que quando é feita com uma lista do Python (linha 245). Dentro do loop externo, a inicialização do grid[item+1] é 4,5 vezes mais rápida para um array do NumPy (linha 276) do que para uma lista (linha 248). Até agora, tudo bem.
No entanto, a execução da linha 279 é 1,5 vezes mais lenta do que seu análogo sem o NumPy na linha 252. O problema é que list comprehension cria uma lista de valores, mas armazenamos esses valores em um array do NumPy que é encontrado no lado esquerdo da expressão. Portanto, essa linha adiciona implicitamente uma sobrecarga de conversão de uma lista em um array do NumPy. Com a linha 279 respondendo por 99,9% do tempo de execução, todas as vantagens do NumPy observadas anteriormente tornam-se insignificantes.
Ainda precisamos, porém, de uma maneira de iterar por meio de arrays para fazer cálculos. Já aprendemos que list comprehension é a ferramenta de iteração mais rápida. A propósito, se você tentar construir um array do NumPy dentro de um bom e velho loop for, evitando a conversão de lista para array do NumPy, obterá o impressionante tempo de execução de 295 segundos. Então, estamos travados e o NumPy é inútil? Claro que não.

Uso adequado do NumPy
Apenas armazenar dados em arrays do NumPy não adianta. O verdadeiro poder do NumPy vem com as funções que executam cálculos em arrays do NumPy. Elas pegam arrays como parâmetros e retornam arrays como resultados.
Por exemplo, existe a função where(), que recebe três arrays como parâmetros: condition, x, e y, e retorna um array construído pela seleção de elementos de x ou de y. O primeiro parâmetro, condition, é um array de booleanos. Ele diz de onde escolher: se um elemento de condition for avaliado como True, o elemento correspondente de x é enviado para a saída, caso contrário, o elemento de y é selecionado.
Observe que a função do NumPy faz tudo isso em uma única chamada. Percorrer os arrays passa a ser um processo integrado.
É assim que usamos where() como um substituto do loop for interno no primeiro solucionador ou, respectivamente, o list comprehension do último:
def solve_numpy_func(capacity, items, weights, values):
grid = np.empty((items + 1, capacity + 1), dtype=int)
grid[0] = 0
for item in range(items):
this_weight = weights[item]
this_value = values[item]
grid[item+1, :this_weight] = grid[item, :this_weight]
temp = grid[item, :-this_weight] + this_value
grid[item + 1, this_weight:] =
np.where(temp > grid[item, this_weight:],
temp,
grid[item, this_weight:])
solution_value = grid[items, capacity]
solution_weight = 0
taken = []
k = capacity
for item in range(items, 0, -1):
if grid[item][k] != grid[item - 1][k]:
taken.append(item - 1)
k -= weights[item - 1]
solution_weight += weights[item-1]
return solution_value, solution_weight, takenExistem três trechos de códigos interessantes: linha 8, linha 9 e linhas 11-13, conforme numeradas acima. Juntas, elas substituem o loop interno que percorreria todos os tamanhos possíveis de mochilas para encontrar os valores da solução.
Até que a capacidade da mochila atinja o peso do item recém adicionado ao conjunto de trabalho (this_weight), devemos ignorar esse item e definir os valores da solução para os do conjunto de trabalho anterior. Isso é bastante direto (linha 8):
grid[item+1, :this_weight] = grid[item, :this_weight]Em seguida, construímos um array auxiliar temp (linha 9):
temp = grid[item, :-this_weight] + this_valueEsse código é análogo, mas muito mais rápido do que:
[grid[item, k — this_weight] + this_value
for k in range(this_weight, capacity+1)]Ele calcula possíveis valores de solução se o novo item for levado para cada uma das mochilas que podem acomodar esse item.
Observe como o array temp é construído adicionando um escalar a um array. Esse é outro recurso poderoso do NumPy chamado "broadcasting". Quando o NumPy vê operandos com dimensões diferentes, ele tenta expandir (ou seja, "transmitir" – em inglês, broadcast) o operando de baixa dimensão para corresponder às dimensões do outro. Em nosso caso, o escalar é expandido para um array do mesmo tamanho que grid[item, :-this_weight] e esses dois arrays são somados. Como resultado, o valor de this_value é adicionado a cada elemento de grid[item, :-this_weight] — nenhum loop é necessário.
Na próxima parte (linhas 10–13), usamos a função where(), que faz exatamente o que é exigido pelo algoritmo: compara dois possíveis valores de solução para cada tamanho de mochila e seleciona aquele que é maior.
grid[item + 1, this_weight:] =
np.where(temp > grid[item, this_weight:],
temp,
grid[item, this_weight:])A comparação é feita pelo parâmetro condition, que é calculado como temp > grid[item, this_weight:]. Essa é uma operação elementar que produz um array de valores booleanos, um para cada tamanho de uma mochila auxiliar. Um valor True significa que o item correspondente deve ser colocado na mochila. Portanto, o valor da solução obtido do array é o segundo argumento da função temp. Caso contrário, o item deve ser ignorado, e o valor da solução é copiado da linha anterior da grade - o terceiro argumento da função where().
Por fim, o motor de dobra foi ativado! Esse solucionador é executado em 0,55 s. Isso é 145 vezes mais rápido que o solucionador baseado em list comprehension e 329 vezes mais rápido que o código utilizando o loop for. Embora não tenhamos ultrapassado o solucionador escrito em Go (0,4 s), chegamos bem perto disso.
Alguns loops são pra ficar
Espere, mas e o loop for externo?
Em nosso exemplo, o código do loop externo, que não faz parte do loop interno, é executado apenas 100 vezes, para que possamos escapar sem mexer nele. No entanto, outras vezes, o loop externo pode ser tão longo quanto o interno.
Podemos reescrever o loop externo usando uma função do NumPy de maneira semelhante ao que fizemos para o loop interno? A resposta é não.
Apesar de ambos serem loops for, os loops externo e interno são bem diferentes no que fazem.
O loop interno produz um array 1D baseado em outro array 1D cujos elementos são todos conhecidos quando o loop começa. É essa disponibilidade prévia dos dados de entrada que nos permitiu substituir o loop interno por map(), list comprehension ou uma função do NumPy.
O loop externo produz um array 2D a partir de um array 1D, cujos elementos não são conhecidos quando o loop começa. Além disso, esses componentes de arrays são calculados por um algoritmo recursivo: podemos encontrar os elementos (i+1)º do array somente depois de encontrarmos o iº.
Suponha que o loop externo possa ser apresentado como uma função:grid = g(row0, row1, … rowN)
Todos os parâmetros da função devem ser avaliados antes que a função seja chamada, mas somente row0 é conhecida de antemão. Como o cálculo da (i+1)ª linha depende da disponibilidade da i-ésima, precisamos de um loop indo de 1 a N para calcular todos os parâmetros da linha. Portanto, para substituir o loop externo com uma função, precisamos de outro loop que avalie os parâmetros dessa função. Esse outro loop é exatamente o loop que estamos tentando substituir.
A outra maneira de evitar o loop for externo é usar recursão. Pode-se facilmente escrever a função recursiva calculate(i) que produz a i-ésima linha da grade. Para fazer o trabalho, a função precisa conhecer a (i-1)ª linha, portanto, chama a si mesma como calculate(i-1) e, em seguida, calcula a i-ésima linha usando as funções do NumPy como fizemos anteriormente. Todo o loop externo pode então ser substituído por calculate(N). Para tornar a imagem completa, um solucionador de mochila recursivo pode ser encontrado no código-fonte que acompanha este artigo no GitHub.
No entanto, a abordagem recursiva claramente não é escalável. O Python não é otimizado para a recursão de cauda. A profundidade da pilha de recursão é, por padrão, limitada pela ordem de mil. Esse limite é certamente conservador, mas, quando exigimos uma profundidade de milhões, o estouro da pilha é altamente provável. Além disso, o experimento mostra que a recursão nem mesmo fornece uma vantagem de desempenho sobre um solucionador baseado em NumPy com o loop for externo.
É aqui que esgotamos as ferramentas fornecidas pelo Python e suas bibliotecas (pelo que sei). Se for absolutamente necessário acelerar o loop que implementa um algoritmo recursivo, será preciso recorrer ao Cython, ou a uma versão do Python compilada em JIT, ou a outra linguagem.
Aprendizados
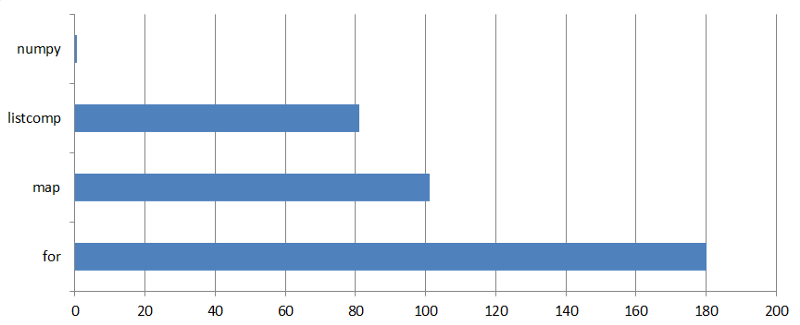
- Faça cálculos numéricos com as funções do Numpy. Elas são duas ordens de magnitude mais rápidas do que as ferramentas integradas do Python.
- Das ferramentas integradas do Python, list comprehension é mais rápida que
map(), que é significativamente mais rápido quefor. - Para algoritmos profundamente recursivos, os loops são mais eficientes do que as chamadas recursivas de funções.
- Você não pode substituir loops recursivos por
map(), list comprehension ou uma função do NumPy. - O código "burro" (dividido em operações elementares) é o mais lento. Use funções e ferramentas integradas.

