Artigo original: SVM Machine Learning Tutorial – What is the Support Vector Machine Algorithm, Explained with Code Examples
A maioria das tarefas que o aprendizado de máquina realiza atualmente inclui coisas como classificar imagens, traduzir idiomas, lidar com grandes quantidades de dados de sensores e prever valores futuros com base em valores atuais. Você pode escolher diferentes estratégias para se adequar ao problema que está tentando resolver.
A boa notícia? Existe um algoritmo em aprendizado de máquina que lidará com praticamente todos os dados que você puder lançar nele. Chegaremos lá em um minuto.
Aprendizado supervisionado x não supervisionado
Duas das estratégias mais comumente usadas em aprendizado de máquina incluem aprendizado supervisionado e aprendizado não supervisionado.
O que é o aprendizado supervisionado?
O aprendizado supervisionado ocorre quando você treina um modelo de aprendizado de máquina usando dados rotulados. Isso significa que você tem dados que já possuem a classificação correta associada a eles. Um uso comum do aprendizado supervisionado é ajudá-lo a prever valores para novos dados.
Com o aprendizado supervisionado, você precisará reconstruir seus modelos à medida que obtém novos dados, para garantir que as previsões retornadas ainda sejam precisas. Um exemplo de aprendizado supervisionado seria rotular imagens de alimentos. Você poderia ter um conjunto de dados dedicado apenas a imagens de pizza para ensinar ao seu modelo o que é uma pizza.
O que é o aprendizado não supervisionado?
O aprendizado não supervisionado ocorre quando você treina um modelo com dados não rotulados. Isso significa que o modelo terá que encontrar suas próprias características e fazer previsões com base em como os dados são classificados.
Um exemplo de aprendizado não supervisionado seria fornecer ao seu modelo imagens de vários tipos de alimentos sem rótulos. O conjunto de dados teria imagens de pizza, batatas fritas e outros alimentos, e você poderia utilizar algoritmos diferentes para fazer com que o modelo identificasse apenas as imagens de pizza sem nenhum rótulo.
Então, o que é um algoritmo?
Quando você ouvir pessoas falando sobre algoritmos de aprendizado de máquina, lembre-se de que elas estão falando sobre diferentes equações matemáticas.
Um algoritmo é apenas uma função matemática personalizável. É por isso que a maioria dos algoritmos possui coisas como funções de custo, valores de peso e parâmetros de funções que você pode alterar com base nos dados com os quais está trabalhando. Basicamente, o aprendizado de máquina é apenas um monte de equações matemáticas que precisam ser resolvidas muito rapidamente.
É por isso que existem tantos algoritmos diferentes para lidas com diferentes tipos de dados. Um algoritmo em particular é a máquina de vetores de suporte (SVM, do inglês support vector machine) e é isso que este artigo abordará em detalhes.
O que é SVM?
Máquinas de vetores de suporte são um conjunto de métodos de aprendizado supervisionado utilizados para classificação, regressão, e detecção de outliers. Todas essas são tarefas comuns em aprendizado de máquina.
Você pode utilizá-los para detectar células cancerígenas com base em milhões de imagens ou para prever futuras rotas de direção com um modelo de regressão bem ajustado.
Existem tipos específicos de SVMs que você pode usar para problemas específicos de aprendizado de máquina, como vetor de suporte de regressão (SVR, do inglês support vector regression), que é uma extensão de vetor de suporte de classificação (SVC, do inglês support vector classification).
A principal coisa a se ter em mente aqui é que essas são apenas equações matemáticas ajustadas para fornecer a resposta mais precisa o mais rapidamente possível.
SVMs são diferentes de outros algoritmos de classificação devido à maneira como escolhem a fronteira de decisão (do inglês, decision boundary) que maximiza a distância dos pontos de dados mais próximo de todas as classes. A fronteira de decisão criada pelos SVMs é chamada de classificador de margem máxima ou o hiperplano de margem máxima.
Como funciona um SVM
Um classificador SVM linear simples funciona criando uma linha reta entre duas classes. Isso significa que todos os pontos de dados de um lado da linha representarão uma categoria, e os pontos de dados do outro lado da linha serão colocados em uma categoria diferente. Isso significa que pode haver um número infinito de linhas para escolher.
O que torna o algoritmo SVM linear melhor do que alguns dos outros algoritmos, como o k-vizinhos mais próximos, é que ele escolhe a melhor linha para classificar seus pontos de dados. Ele escolhe a linha que separa os dados e que fica o mais distante possível dos pontos de dados mais próximos.
Um exemplo 2D ajuda a entender todo o jargão do aprendizado de máquina. Basicamente, você tem alguns pontos de dados em uma grade. Você está tentando separar esses pontos de dados pela categoria em que eles deveriam se enquadrar, mas você não quer ter nenhum dado na categoria errada. Isso significa que você está tentando encontrar a linha entre os dois pontos mais próximos que mantém os outros pontos de dados separados.
Portanto, os dois pontos de dados mais próximos fornecem os vetores de suporte que você usará para encontrar essa reta. Essa linha é chamada de limite de decisão.
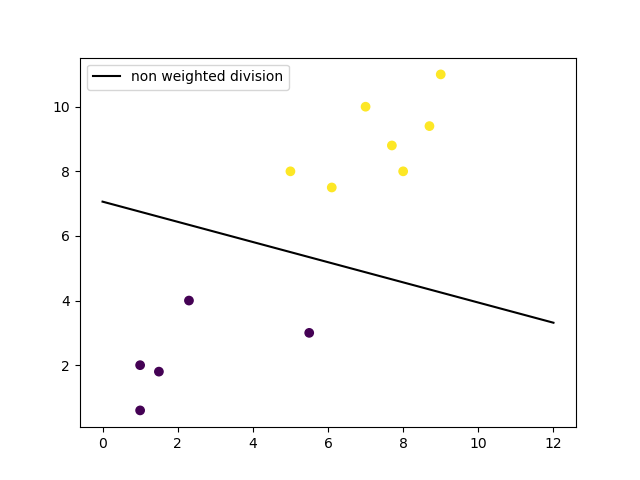
O limite de decisão não precisa ser uma linha. Também é chamado de hiperplano, porque você pode encontrar o limite de decisão com qualquer número de recursos, não apenas dois.
Tipos de SVMs
Existem dois tipos diferentes de SVMs, cada um usado para coisas diferentes:
- SVM simples: normalmente usado para regressão linear e problemas de classificação.
- SVM kernel: tem mais flexibilidade para dados não lineares porque você pode adicionar mais recursos para ajustar um hiperplano em vez de um espaço bidimensional.
Por que SVMs são usados em aprendizado de máquina?
SVMs são usados em aplicações como reconhecimento de escrita, detecção de intrusão, reconhecimento facial, classificação de e-mail, classificação de genes, e em páginas da web. Essa é uma das razões pelas quais usamos SVMs no aprendizado de máquina. Ele pode lidar tanto com classificação quanto regressão em dados lineares e não lineares.
Outra razão pela qual usamos SVMs é o fato de que eles podem encontrar relações complexas entre seus dados sem que você precise fazer muitas transformações por conta própria. É uma ótima opção quando você trabalha com conjuntos de dados menores, que possuem dezenas a centenas de milhares de recursos. Eles normalmente encontram resultados mais precisos quando comparados a outros algoritmos devido à sua capacidade de lidar com conjuntos de dados pequenos e complexos.
Aqui estão alguns dos prós e contras do uso de SVMs.
Prós
- Eficaz em conjuntos de dados com múltiplas características, como dados financeiros ou médicos.
- Eficaz nos casos em que o número de recursos é maior que o número de pontos de dados.
- Usa um subconjunto de pontos de treinamento na função de decisão chamados vetores de suporte, o que o torna eficiente em termos de memória.
- Diferentes funções de kernel podem ser especificadas para a função de decisão. Você pode usar kernels comuns, mas também é possível especificar kernels personalizados.
Contras
- Se o número de características for muito maior que o número de pontos de dados, é crucial evitar o sobreajuste (em inglês, overfitting) ao escolher as funções do kernel e o termo de regularização.
- SVMs não fornecem estimativas de probabilidade diretamente. Elas são calculados usando uma cara validação cruzada quíntupla.
- Funciona melhor em pequenos conjuntos de amostras devido ao seu alto tempo de treinamento.
Como os SVMs podem usar qualquer número de kernels, é importante que você conheça alguns deles.
Funções do kernel
Linear
Eles são comumente recomendados para classificação de texto, pois a maioria desses tipos de problemas de classificação são linearmente separáveis.
O kernel linear funciona muito bem quando há muitas características, e os problemas de classificação de texto têm muitas características. As funções lineares do kernel são mais rápidas que a maioria das outras e você tem menos parâmetros para otimizar.
Aqui está a função que define o kernel linear:
f(X) = w^T * X + bNesta equação, w é o vetor de peso (do inglês, weight) que você deseja minimizar, X são os dados que você está tentando classificar e b é o coeficiente linear estimado a partir dos dados de treinamento. Esta equação define o limite de decisão que o SVM retorna.
Polinomial
O kernel polinomial não é usado na prática com muita frequência porque não é tão eficiente computacionalmente quanto outros kernels e suas previsões não são tão precisas.
Aqui está a função para um kernel polinomial:
f(X1, X2) = (a + X1^T * X2) ^ bEssa é uma das equações polinomiais de kernel mais simples que você pode usar. f(X1, X2) representa o limite de decisão polinomial que separará seus dados. X1 e X2 representam seus dados.
Função de base radial gaussiana (RBF)
Esse é um dos kernels mais poderosos e comumente usados em SVMs. Ele geralmente é a escolha para dados não lineares.
Aqui está a equação para um kernel RBF:
f(X1, X2) = exp(-gamma * ||X1 - X2||^2)Nesta equação, gama especifica quanto um único ponto de treinamento tem sobre os outros pontos de dados ao seu redor. ||X1 - X2|| é o produto escalar entre seus recursos.
Sigmoide
Mais útil em redes neurais do que em máquinas de vetores de suporte, mas há casos de uso específicos ocasionais.
Aqui está a função para um kernel sigmoide:
f(X, y) = tanh(alpha * X^T * y + C)Nesta função, alfa é um vetor de peso e C é um valor de deslocamento para explicar alguns erros de classificação de dados que podem ocorrer.
Outros
Existem muitos outros kernels que você pode usar em seu projeto. Essa pode ser uma decisão a ser tomada quando você precisar atender a certas restrições de erro, quiser tentar acelerar o tempo de treinamento ou quiser superajustar os parâmetros.
Alguns outros kernels incluem: ANOVA de base radial, tangente hiperbólica e Laplace RBF (texto em inglês).
Agora que você sabe um pouco sobre como os kernels funcionam nos bastidores, vamos ver alguns exemplos.
Exemplos com conjuntos de dados
Para mostrar como os SVMs funcionam na prática, passaremos pelo processo de treinamento de um modelo com ele usando a biblioteca Python Scikit-learn. Essa biblioteca é comumente usada em todos os tipos de problemas de aprendizado de máquina e funciona bem com outras bibliotecas Python.
Aqui estão as etapas encontradas regularmente em projetos de aprendizado de máquina:
- Importe o conjunto de dados
- Explore os dados para descobrir como eles são
- Pré-processe os dados
- Divida os dados em atributos e rótulos
- Divida os dados em conjuntos de treinamento e teste
- Treine o algoritmo SVM
- Faça algumas previsões
- Avalie os resultados do algoritmo
Algumas dessas etapas podem ser combinadas dependendo de como você lida com seus dados. Faremos um exemplo com um SVM linear e um SVM não linear. Você pode encontrar o código para esses exemplos aqui.
Exemplo de SVM linear
Começaremos importando algumas bibliotecas que facilitarão o trabalho com a maioria dos projetos de aprendizado de máquina.
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svmPara um exemplo linear simples, faremos apenas alguns dados fictícios e que atuarão no lugar da importação de um conjunto de dados.
# dados lineares
X = np.array([1, 5, 1.5, 8, 1, 9, 7, 8.7, 2.3, 5.5, 7.7, 6.1])
y = np.array([2, 8, 1.8, 8, 0.6, 11, 10, 9.4, 4, 3, 8.8, 7.5])A razão pela qual estamos trabalhando com arrays numpy é para tornar as operações de matriz mais rápidas, pois elas usam menos memória do que as listas do Python. Você também pode aproveitar a digitação do conteúdo dos arrays. Agora, vamos dar uma olhada na aparência dos dados em um gráfico:
# exibir dados não classificados
plt.scatter(X, y)
plt.show()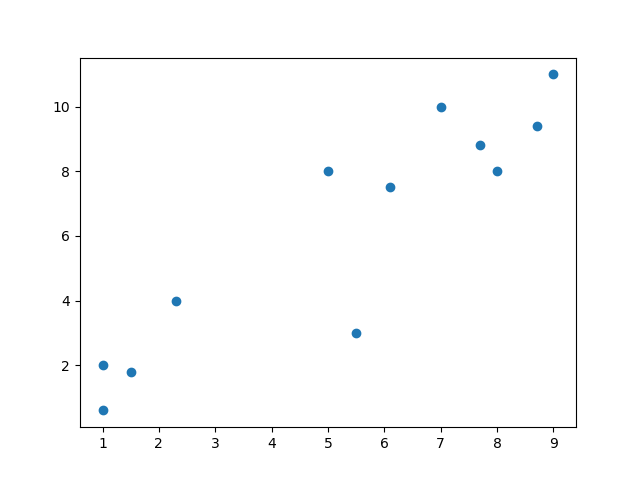
Depois de ver a aparência dos dados, você poderá adivinhar melhor qual algoritmo funcionará melhor para você. Tenha em mente que esse é um conjunto de dados muito simples. Então, na maioria das vezes, você precisará trabalhar em seus dados para colocá-los em um estado utilizável.
Faremos um pré-processamento no código já estruturado. Isso colocará os dados brutos em um formato que podemos usar para treinar o modelo SVM.
# modelando os dados para o treinamento do modelo
training_X = np.vstack((X, y)).T
training_y = [0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1]Agora, podemos criar o modelo SVM usando um kernel linear.
# defina o modelo
clf = svm.SVC(kernel='linear', C=1.0)Essa linha de código acabou de criar um modelo completo de aprendizado de máquina. Agora, só precisamos treiná-lo com os dados que pré-processamos.
# treine o model
clf.fit(training_X, training_y)É assim que você pode construir um modelo para qualquer projeto de aprendizado de máquina. O conjunto de dados que temos pode ser pequeno, mas se você encontrar um conjunto de dados do mundo real que possa ser classificado com um limite linear, esse modelo ainda funcionará.
Com seu modelo treinado, você pode fazer previsões sobre como um novo ponto de dados será classificado e criar um gráfico do limite de decisão. Vamos traçar o limite de decisão.
# obter os valores ponderados para a equação lineara partir do modelo do SVM treinado
w = clf.coef_[0]
# obter o deslocamento de y para a equação linear
a = -w[0] / w[1]
# criar o espaço do eixo x para os pontos de dados
XX = np.linspace(0, 13)
# obter os valores de y para colocar a fronteira de decisão no gráfico
yy = a * XX - clf.intercept_[0] / w[1]
# colocar a fronteira de decisão no gráfico
plt.plot(XX, yy, 'k-')
# exibir o gráfico visualmente
plt.scatter(training_X[:, 0], training_X[:, 1], c=training_y)
plt.legend()
plt.show()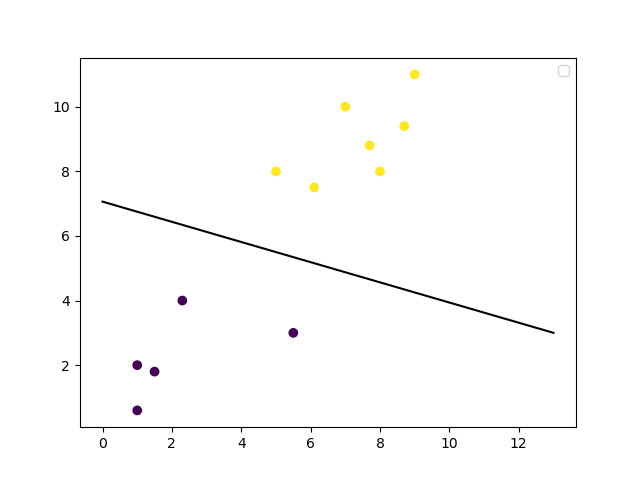
Exemplo de SVM não linear
Neste exemplo, usaremos um conjunto de dados um pouco mais complicado para mostrar uma das áreas em que os SVMs se destacam. Vamos importar alguns pacotes.
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn import svmEsse conjunto de importações é semelhante ao do exemplo linear, exceto que importa mais uma coisa. Agora, podemos usar um conjunto de dados diretamente da biblioteca Scikit-learn.
# dados não lineares
circle_X, circle_y = datasets.make_circles(n_samples=300, noise=0.05)A próxima etapa é dar uma olhada na aparência desses dados brutos em um gráfico.
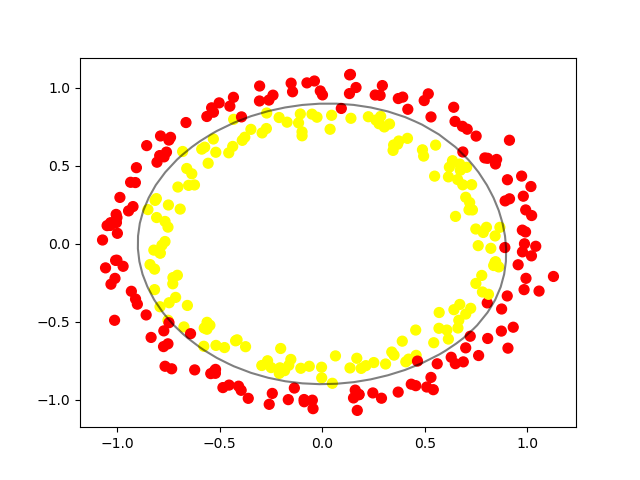
# mostrar os dados não lineares brutos (raw)
plt.scatter(circle_X[:, 0], circle_X[:, 1], c=circle_y, marker='.')
plt.show()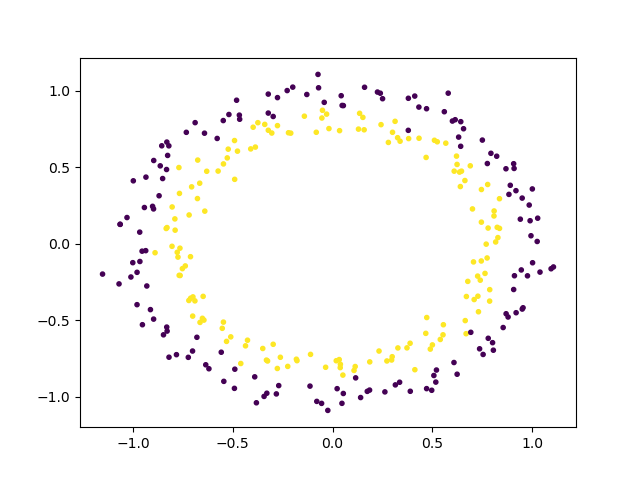
Agora que você pode ver como os dados são separados, podemos escolher um SVM não linear para começar. Esse conjunto de dados não precisa de nenhum pré-processamento antes de usá-lo para treinar o modelo. Portanto, podemos pular essa etapa. Aqui vemos como o modelo SVM ficará para isso:
# criar o algoritmo não linear para o modelo
nonlinear_clf = svm.SVC(kernel='rbf', C=1.0)Nesse caso, usaremos um kernel RBF (Função de Base Radial Gaussiana) para classificar esses dados. Você também pode tentar o kernel polinomial para ver a diferença entre os resultados obtidos. Agora, é hora de treinar o modelo.
# treinamento do modelo não linear
nonlinear_clf.fit(circle_X, circle_y)Você pode começar a rotular novos dados na categoria correta com base nesse modelo. Para ver como é o limite de decisão, teremos que criar uma função personalizada para representá-lo.
# Crie o gráfico para a fronteira de decisão para um problema do SVM não linear
def plot_decision_boundary(model, ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# crie a grade para avaliar o modelo
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
# modele os dados
xy = np.vstack([X.ravel(), Y.ravel()]).T
# obtenha a fronteira de decisão com base no modelo
P = model.decision_function(xy).reshape(X.shape)
# crie o gráfico para a fronteira de decisão
ax.contour(X, Y, P,
levels=[0], alpha=0.5,
linestyles=['-'])Você tem tudo o que precisa para traçar o limite de decisão para esses dados não lineares. Podemos fazer isso com algumas linhas de código que usam a biblioteca Matlibplot, assim como os outros gráficos.
# crie o gráfico para os dados e para a fronteira de decisão
plt.scatter(circle_X[:, 0], circle_X[:, 1], c=circle_y, s=50)
plot_decision_boundary(nonlinear_clf)
plt.scatter(nonlinear_clf.support_vectors_[:, 0], nonlinear_clf.support_vectors_[:, 1], s=50, lw=1, facecolors='none')
plt.show()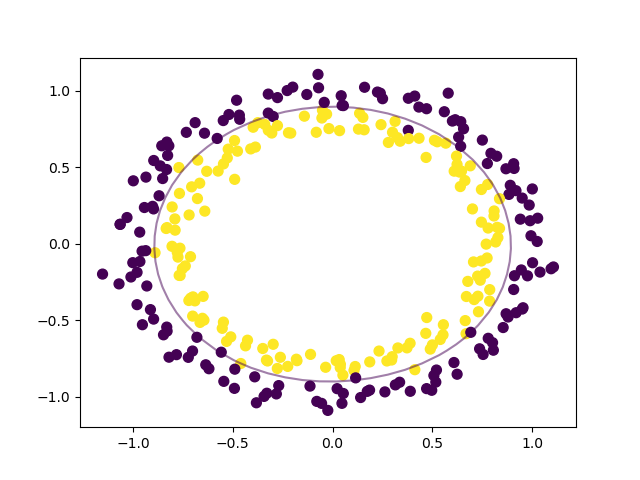
Quando você tem seus dados e conhece o problema que está tentando resolver, tudo pode ser realmente simples assim.
Você pode alterar completamente seu modelo de treinamento, escolher diferentes algoritmos e recursos para trabalhar e ajustar seus resultados com base em vários parâmetros. Existem bibliotecas e pacotes para tudo isso agora, então não há muita matemática com a qual você precise lidar.
Dicas para problemas do mundo real
Os conjuntos de dados do mundo real têm alguns problemas comuns devido ao tamanho que podem ter, aos diversos tipos de dados que contêm e a quanto poder de computação podem precisar para treinar um modelo.
Existem algumas coisas que você deve observar com SVMs em particular:
- Certifique-se de que seus dados estejam em formato numérico em vez de categórico. Os SVMs esperam números em vez de outros tipos de rótulos.
- Evite copiar dados tanto quanto possível. Algumas bibliotecas do Python duplicarão seus dados se eles não estiverem em um formato específico. A cópia de dados também diminuirá o tempo de treinamento e distorcerá a maneira como o modelo atribui os pesos a um recurso específico.
- Observe o tamanho do cache do kernel, pois ele usa sua RAM. Se você tiver um conjunto de dados muito grande, isso poderá causar problemas ao seu sistema.
- Dimensione seus dados, pois os algoritmos SVM não são invariantes à escala. Isso significa que você pode converter todos os seus dados para ficarem dentro dos intervalos de [0, 1] ou [-1, 1].
Outras considerações
Você pode se perguntar por que não entrei em detalhes profundos da matemática aqui. Isso ocorreu, principalmente, pelo fato de que eu não quero assustar as pessoas e impedi-las de aprender mais sobre aprendizado de máquina.
É divertido aprender sobre essas equações matemáticas longas e complicadas e suas derivações, mas é raro você escrever seus próprios algoritmos e provas em projetos reais.
É como ocorre com a maioria das outras coisas que você usa todos os dias, como o telefone ou o computador. Você pode fazer tudo o que precisa sem saber como os processadores são construídos.
O aprendizado de máquina é como qualquer outra aplicação da engenharia de software. Existem vários pacotes que tornam mais fácil obter os resultados necessários sem um conhecimento profundo em estatística.
Depois de praticar um pouco com os diferentes pacotes e bibliotecas disponíveis, você descobrirá que a parte mais difícil do aprendizado de máquina é obter e rotular seus dados.
A autora trabalha em neurociência, aprendizado de máquina e com questões baseadas na web! Siga a autora no Twitter para saber mais a respeito e sobre outras coisas interessantes em tecnologia.

