Artigo original: Finding Shortest Paths using Breadth First Search
Escrito por: Sachin Malhotra
Você sabe qual foi o volume global de tráfego aéreo em 2017? Sabe qual foi o aumento do tráfego aéreo nos últimos anos? Bem, vamos dar uma olhada em alguns dados.
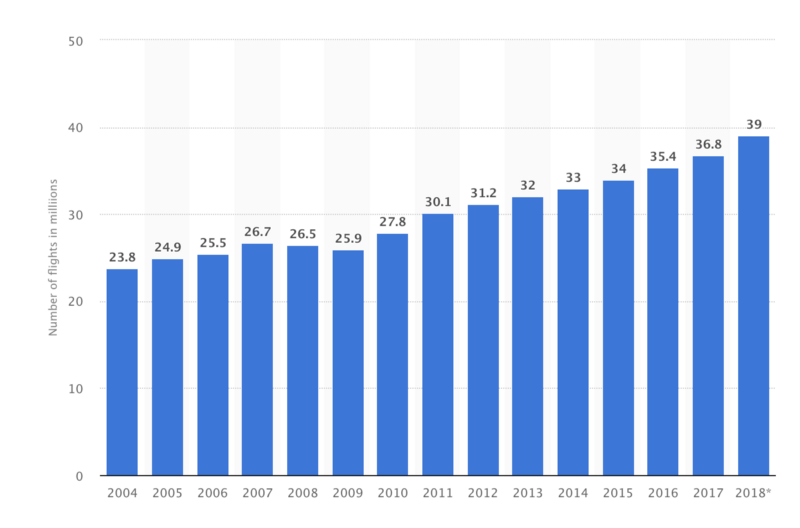
De acordo com a Organização da Aviação Civil Internacional (ICAO), um recorde de 4,1 bilhões de passageiros foram transportados pelo setor de aviação em 2017. Além disso, o número de voos no mundo subiu para 37 milhões em 2017.
São muitos passageiros, e muitos voos ocupando o espaço aéreo diariamente no mundo inteiro. Como existem centenas de milhares desses voos, é provável que existam rotas diferentes que tenham mais de uma parada entre um lugar e outro.
Cada voo tem sua própria origem e destino, bem como um preço padrão de assento de classe econômica associado a ele. Vamos deixar de lado as passagens sofisticadas da classe executiva, o espaço adicional para as pernas e tudo mais!
Nesse cenário, é muito confuso escolher qual voo seria o melhor se quiséssemos ir de um lugar para outro.
Vamos ver o número de opções de voos que o StudentUniverse (oferece descontos para estudantes 😜) me proporciona, partindo de Los Angeles a Nova Délhi.

Estão sendo oferecidos 119 voos no total. Em seguida, aparece um pop-up no site informando que há outros sites que podem estar oferecendo voos semelhantes com tarifas ainda mais baratas. 😩
Uma variedade de sites e incontáveis voos – e estamos falando apenas de uma origem e destino.
Como desenvolvedor, se eu quisesse resolver esse problema, criaria um sistema para atender com eficiência às seguintes consultas:
- Número total de destinos acessíveis (com um número máximo de paradas) a partir da minha localização atual, listando também esses destinos.
É preciso manter as opções em aberto quando se deseja viajar 😃. - É um fato conhecido (minha opinião 😉) que rotas com escalas tendem a ser mais baratas que voos diretos.
Assim, dada uma origem e um destino, podemos querer encontrar rotas com pelo menos 2 ou 3 paradas. - Mais importante: qual é a rota mais barata, dada uma origem e destino?
- E.... bem, vamos deixar isso pro final 🙈.
Como você pode imaginar, existiriam potencialmente milhares de voos como resultado das duas primeiras consultas. Certamente, porém, podemos reduzir isso fornecendo alguns outros critérios para diminuir o tamanho do resultado. Para o escopo deste artigo, vamos nos concentrar nesses tipos de consultas.
Modelando a rede aérea como um grafo
O título deste artigo deixa bem claro que os grafos estariam envolvidos em algum lugar, não é mesmo?
Modelar esse problema como um problema de travessia de grafo simplifica bastante, tornando-o muito mais fácil de ser tratado. Portanto, como primeira etapa, vamos definir nosso grafo.
Modelamos o tráfego aéreo como um grafo:
- direcionado
- possivelmente cíclico
- ponderado
- de floresta. G (V, E)
Direcionado porque cada voo terá uma origem e destino designados. Isso significa muita coisa.
Cíclico porque há grande possibilidade de encontrar vários voos que partam de um determinado local e terminem no mesmo local.
Ponderado porque cada voo tem um custo associado a ele – no caso, poderia ser o custo da passagem aérea da classe econômica citada no início deste artigo.
Por fim, é um grafo de floresta porque podemos ter múltiplos componentes conectados. Não é necessário que todas as cidades do mundo tenham algum tipo de rede aérea entre elas. Assim, o grafo pode ser desconectado e, portanto, uma floresta.
Os vértices, V, seriam os locais em todo o mundo onde há aeroportos em funcionamento.
As arestas, E (do inglês, edges), representariam todos os voos que constituem o tráfego aéreo. Uma aresta u --> v simplesmente significa que você tem um voo direcionado da localização/nó u até v .
Agora que temos uma ideia de como modelar a rede aérea em um grafo, vamos prosseguir e resolver a primeira consulta básica que um usuário pode ter.
Número total de destinos acessíveis
Quem não gosta de viajar?
Como alguém que gosta de explorar lugares diferentes, seria interessante saber quais destinos são acessíveis a partir de seu aeroporto local. Novamente, haveria critérios adicionais aqui para reduzir os resultados dessa consulta. Para fins didáticos, vamos apenas encontrar todos os locais acessíveis a partir de nosso aeroporto local.
Agora que temos um grafo bem definido, podemos aplicar algoritmos de travessia para o computar.
A partir de um determinado ponto, podemos usar a busca em largura (BFS, do inglês, Breadth-First Search) ou a busca em profundidade (DFS, do inglês, Depth-First Search) para examinar o grafo ou os locais acessíveis a partir da localização inicial que tenham um número máximo de paradas. Como este artigo trata exclusivamente do algoritmo de busca em largura, vamos ver como podemos usar o famoso BFS para realizar essa tarefa.
Vamos inicializar a fila do BFS com o local fornecido como o ponto de partida. Em seguida, executamos o primeiro percurso em largura e continuamos até que a fila esteja vazia ou até que o número máximo de paradas tenha se esgotado.
Observação: se você não estiver familiarizado com a busca em largura ou com a em profundidade, recomendo que leia este artigo (texto em inglês) antes de continuar.
Vamos dar uma olhada no código que inicializa a nossa estrutura de dados do grafo. Também precisamos analisar como o algoritmo do BFS acabaria nos fornecendo todos os destinos acessíveis a partir de uma determinada origem.
from collections import defaultdict
from pprint import pprint
class FlightNetwork:
def __init__(self):
self.neighbors = defaultdict(list)
self.cost = defaultdict(list)
def add_flight(self, source, destination, price):
self.neighbors[source].append(destination)
self.cost[source].append(price)
def show_flights(self):
print("Destinos:");pprint(dict(self.neighbors))
print("Custo:");pprint(dict(self.cost))
f = FlightNetwork()
f.add_flight('Los Angeles', 'New Delhi', 200)
f.add_flight('Los Angeles', 'Japan', 87)
f.add_flight('Germany', 'New Delhi', 125)
f.add_flight('Italy', 'Los Angeles', 150)
f.add_flight('New Delhi', 'France', 100)
f.add_flight('Los Angeles', 'France', 200)
f.add_flight('Italy', 'New Delhi', 300)
f.add_flight('France', 'Norway', 175)
f.add_flight('Ireland', 'Chicago', 100)
f.add_flight('Chicago', 'Italy', 135)
f.add_flight('Los Angeles', 'Ireland', 100)
f.add_flight('Ireland', 'New Delhi', 200)
f.show_flights()
Destinos:
{
'Chicago': ['Italy'],
'France': ['Norway'],
'Germany': ['New Delhi'],
'Ireland': ['Chicago', 'New Delhi'],
'Italy': ['Los Angeles', 'New Delhi'],
'Los Angeles': ['New Delhi', 'Japan', 'France', 'Ireland'],
'New Delhi': ['France']
}
Custo:
{
'Chicago': [135],
'France': [175],
'Germany': [125],
'Ireland': [100, 200],
'Italy': [150, 300],
'Los Angeles': [200, 87, 200, 100],
'New Delhi': [100]
}Agora que temos uma boa ideia de como o grafo deve ser inicializado, vamos dar uma olhada no código do algoritmo do BFS.
Executando o bfs na cidade de Los Angeles, o resultado seriam os seguintes destinos acessíveis:
{'Chicago', 'France', 'Ireland', 'Italy', 'Japan', 'New Delhi', 'Norway'}Isso foi simples, não?
Veremos como podemos limitar o BFS a um número máximo de paradas mais adiante neste artigo.
Se tivéssemos uma rede aérea enorme, que é o que teríamos em um cenário de produção, então não desejaríamos necessariamente saber todos os destinos possíveis de um determinado ponto de partida.
Esse é um caso de uso quando a rede aérea for muito pequena ou pertencer apenas a poucas regiões dos Estados Unidos.
Porém, para uma rede grande, um caso de uso mais realista seria encontrar todas as rotas de voo que possuem várias paradas. Vamos examinar esse problema mais a fundo e ver como podemos resolvê-lo.
Rotas com múltiplas paradas
É um fato bastante conhecido que, normalmente, para uma determinada origem e destino, uma viagem com múltiplas paradas é mais barata que um voo direto, sem escalas.
Muitas vezes, preferimos o voo direto para evitar as escalas, em especial porque os voos com várias paradas tendem a tomar muito tempo – o que não temos.
No entanto, se você não tiver nenhum compromisso urgente e quiser economizar algum dinheiro (e se sentir confortável com o voo que tem escalas – opção oferecida por diversas companhias aéreas) poderá, na verdade, se beneficiar muito ao fazer essa escolha.
Você pode passar por alguns dos lugares mais bonitos do mundo com seus modernos aeroportos. Isso já pode ser motivação o suficiente.
Em termos do modelo de grafo sobre o qual estávamos falando, dada uma origem e um destino, precisamos criar rotas com 2 ou mais paradas para uma origem e destino fornecidos.
Para um usuário final, pode ser que a resposta abaixo não seja a melhor:
[A, C, D, B], 2 paradas, $X
[A, E, D, C, F, W, G, T, B], 8 paradas, $M
[A, R, E, G, B], 3 paradas, $K
[A, Z, X, C, V, B, N, S, D, F, G, H, B, 11 paradas, $PEu sei. Ninguém em sã consciência escolheria um voo com 11 paradas, mas o que estou tentando dizer é que um usuário final espera simetria. Ou seja, ele desejaria ver primeiro todos os voos com 2 paradas, depois todos os voos com 3 e assim por diante até um máximo de, digamos, 5 paradas.
Porém, todas as rotas de voo com o mesmo número de paradas entre elas devem ser exibidas juntas. Esse é um requisito necessário.
Então, vamos ver como podemos resolver isso. Dado um grafo de redes aéreas, um ponto de partida S (do inglês, source) e um destino D, precisamos realizar um percurso em nível e guardar as rotas de voo de S --> D com pelo menos 2 e no máximo 5 paradas entre elas. Isso quer dizer que precisamos realizar um percurso em nível até uma profundidade de 7 partindo do nó inicial S.
Aqui está o código para resolver esse problema:
{'A': ['C', 'B', 'F'],
'B': ['D'],
'C': ['B', 'M', 'E', 'F'],
'D': ['C', 'E', 'F'],
'E': ['F'],
'M': ['F']}
Custo:
{'A': [10, 20, 14],
'B': [20],
'C': [120, 200, 145, 50],
'D': [75, 45, 60],
'E': [60],
'M': [45]}
parent = f.level_order_traversal('A', 'F', (2,5))
for r in range(2, 6):
print("\nOs voos com {} paradas no meio são os seguintes:".format(r))
routes = f.get_route(('F', r), 'A', parent)
for r in routes:
print(r)
Os voos com 2 paradas no meio são os seguintes:
A-->C-->M-->F
A-->C-->E-->F
A-->B-->D-->F
Os voos com 3 paradas no meio são os seguintes:
A-->C-->B-->D-->F
A-->B-->D-->C-->F
A-->B-->D-->E-->F
Os voos com 4 paradas no meio são os seguintes:
A-->C-->B-->D-->C-->F
A-->C-->B-->D-->E-->F
A-->B-->D-->C-->E-->F
A-->B-->D-->C-->M-->F
A-->C-->B-->D-->E-->F
A-->B-->D-->C-->E-->F
Os voos com 5 paradas no meio são os seguintes:
A-->C-->B-->D-->C-->M-->F
A-->C-->B-->D-->C-->E-->F
A-->B-->D-->C-->B-->D-->FEssa pode não ser a melhor maneira de resolver esse problema quando ele for muito grande – uma grande restrição de memória aconteceria por conta dos nós presentes na fila no momento.
Como cada nó, ou localização, pode ter milhares de voos para diferentes destinos do mundo, a fila poderia se tornar enorme se fôssemos armazenar dados reais de voos dessa maneira. Esse exemplo é apenas para demonstrar um dos casos de uso do algoritmo de busca em largura.
Por agora, vamos nos concentrar apenas no percurso e ver o que acontece na prática. O algoritmo de percurso é simples, porém, toda a complexidade espacial do percurso em nível se dá graças a elementos presentes na fila e de seu tamanho.
Existem muitas formas de se implementar esse algoritmo. Além disso, cada uma delas varia em termos de consumo máximo memória em determinado momento pelos elementos presentes na fila.
Queremos saber o consumo máximo de memória da fila em um dado momento durante o percurso em nível. Antes disso, vamos construir uma rede aérea aleatória com preços aleatórios.
from collections import defaultdict
import random
from pprint import pprint
def add_edge(s, d, adj_list):
adj_list[s].append(d)
nodes = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
adj_list = defaultdict(list)
for i, s in enumerate(nodes[:5]):
for i in range(10 - i):
while True:
d = (nodes[random.randint(0, 8)], "$"+str(random.randint(50, 500)))
if d[0] != s:
break
add_edge(s, d, adj_list)Agora a implementação do percurso em nível.
import sys
def level_order_naive(source, max_level):
queue = [(source, 0)]
max_memory = 0
levels = []
while queue:
max_memory = max(max_memory, sum(list(map(sys.getsizeof, queue))))
element, level = queue.pop(0)
levels.append((element, level))
if level == max_level:
continue
if element in adj_list:
for neighbor in adj_list[element]:
queue.append((neighbor[0], level + 1))
return max_memory, levels Essa, por sinal, é a implementação mais simples e direta do algoritmo de percurso em nível.
Junto a cada nó que adicionamos à fila, armazenamos também as informações de nível e uma tupla de (nó, nível) dentro da fila. Assim, toda a vez que removermos um elemento da fila, teremos as informações do nível em que estava.
As informações de nível, para nosso caso de uso, são o número de paradas desde a origem até esse local específico em nossa rota de voo.
A questão é que podemos fazer otimizações, já que consumo de memória no programa precisa ser levado em consideração. Aqui está uma abordagem um pouco melhorada de como se fazer o percurso em nível.
def level_order_NULL(source, max_level):
queue = [source, None]
max_memory = 0
level = 0
levels = []
while queue:
max_memory = max(max_memory, sum(list(map(sys.getsizeof, queue))))
element = queue.pop(0)
if element:
levels.append((element, level))
if level == max_level:
continue
if not element:
level += 1
queue.append(None)
continue
if element in adj_list:
for neighbor in adj_list[element]:
queue.append(neighbor[0])
return max_memory, levels A ideia aqui é que não vamos armazenar nenhuma informação extra aos nós que estão sendo adicionados na fila. Usamos um objeto None para marcar o fim do nível. Não sabemos o tamanho de nenhum nível de antemão a não ser o do primeiro nível, que tem apenas o nosso nó source.
Assim, iniciamos a fila com [source, None] e continuamos a remover elementos. Toda vez que encontramos um elemento None, saberemos que o nível terminou e que o seguinte começou. Adicionamos outro None para marcar o final desse novo nível.
Considere o simples grafo abaixo. Vamos ver rapidamente como isso funcionaria na prática.
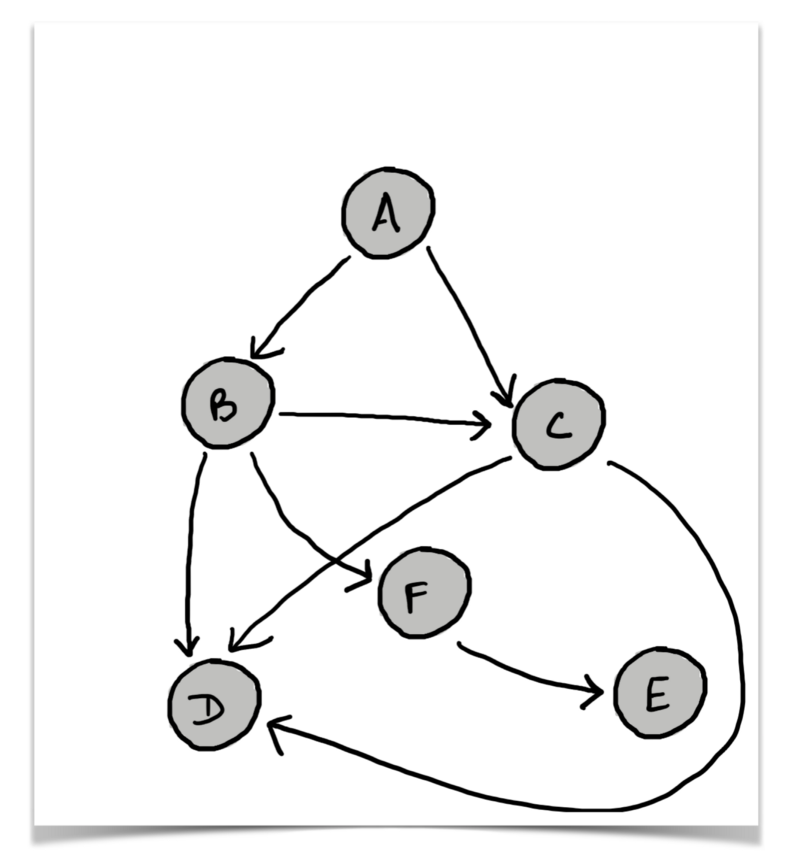
**************************************************** LEVEL 0 begins
level = 0, queue = [A, None]
level = 0, pop, A, push, B, C, queue = [None, B, C]
pop None ******************************************* LEVEL 1 begins
push None
level = 1, queue = [B, C, None]level = 1, pop, B, push, C, D, F, queue = [C, None, C, D, F]
level = 1, pop, C, push, D, D (lol!), queue = [None, C, D, F, D, D]
pop None ******************************************* LEVEL 2 begins
push None
level = 2, queue = [C, D, F, D, D, None] .... e assim por dianteEspero que a explicação tenha esclarecido o funcionamento do algoritmo. Esse certamente é um método interessante de se fazer o percurso em nível, monitorar níveis e não se preocupar muito com o uso de memória. Sem dúvida, reduz o volume de memória usado pelo código.
Porém, não fique muito entusiasmado pensando que isso foi uma melhoria significativa.
Quero dizer, é significativa, mas você deveria estar se fazendo duas perguntas:
- De que tamanho foi essa melhoria?
- Podemos melhorar ainda mais?
Vou responder as duas e começarei pela segunda. A resposta é Sim!
Podemos fazer uma melhoria aqui ao eliminar completamente a necessidade do None dentro da fila. A motivação para essa abordagem vem da própria abordagem anterior.
Se você observar atentamente o algoritmo acima, perceberá que toda vez que retiramos um None, um nível é concluído e outro está pronto para ser processado. O importante é que exista um nível seguinte inteiro dentro da fila no momento em que ocorre a remoção do None. Podemos utilizar essa ideia de considerar o tamanho da fila na lógica do percurso.
Aqui está o pseudocódigo desse algoritmo otimizado:
queue = Queue()
queue.push(S)
level = 0
while queue is not empty {
size = queue.size()
// size representa o número de elementos no nível atual
for i in 1..size {
element = queue.pop()
// Processe o elemento aqui
// Realize uma série de operações queue.push() aqui
level += 1Aqui está o código dele.
def level_order_queue_size(source, max_level):
queue = [source]
max_memory = 0
levels = []
level = 0
while queue:
max_memory = max(max_memory, sum(list(map(sys.getsizeof, queue))))
size = len(queue)
for _ in range(size):
element = queue.pop(0)
levels.append((element, level))
if level == max_level:
continue
if element in adj_list:
for neighbor in adj_list[element]:
queue.append(neighbor[0])
level += 1
return max_memory, levels O pseudocódigo é autoexplicativo. Basicamente, eliminamos a necessidade de um elemento None por nível e, ao invés disso, usamos o tamanho da fila para mudar de nível. Isso também leva a uma melhoria em relação ao último método, mas em que proporção?
Dê uma olhada no Jupyter Notebook a seguir para ver a diferença de consumo de memória entre os três métodos.
from collections import defaultdict
import random
from pprint import pprint
def add_edge(s, d, adj_list):
adj_list[s].append(d)
nodes = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
adj_list = defaultdict(list)
for i, s in enumerate(nodes[:5]):
for i in range(10 - i):
while True:
d = (nodes[random.randint(0, 8)], "$"+str(random.randint(50, 500)))
if d[0] != s:
break
add_edge(s, d, adj_list)
adj_list['A']
[('G', '$418'), ('F', '$75'), ('H', '$141'), ('D', '$203'), ('D', '$101'), ('I', '$51'), ('G', '$187'), ('H', '$137'), ('F', '$425'), ('F', '$69')]
import sys
def level_order_naive(source, max_level):
queue = [(source, 0)]
max_memory = 0
levels = []
while queue:
max_memory = max(max_memory, sum(list(map(sys.getsizeof, queue))))
element, level = queue.pop(0)
levels.append((element, level))
if level == max_level:
continue
if element in adj_list:
for neighbor in adj_list[element]:
queue.append((neighbor[0], level + 1))
return max_memory, levels
max_memory, levels = level_order_naive('A', 5)
max_memory, levels[50:60],len(levels)
(20224, [('H', 3), ('I', 3), ('D', 3), ('B', 3), ('B', 3), ('A', 3), ('B', 3), ('F', 3), ('I', 3), ('G', 3)], 523)
def level_order_NULL(source, max_level):
queue = [source, None]
max_memory = 0
level = 0
levels = []
while queue:
max_memory = max(max_memory, sum(list(map(sys.getsizeof, queue))))
element = queue.pop(0)
if element:
levels.append((element, level))
if level == max_level:
continue
if not element:
level += 1
queue.append(None)
continue
if element in adj_list:
for neighbor in adj_list[element]:
queue.append(neighbor[0])
return max_memory, levels
max_memory, levels = level_order_NULL('A', 5)
max_memory, levels[50:60], len(levels)
(15816, [('H', 3), ('I', 3), ('D', 3), ('B', 3), ('B', 3), ('A', 3), ('B', 3), ('F', 3), ('I', 3), ('G', 3)], 523)
def level_order_queue_size(source, max_level):
queue = [source]
max_memory = 0
levels = []
level = 0
while queue:
max_memory = max(max_memory, sum(list(map(sys.getsizeof, queue))))
size = len(queue)
for _ in range(size):
element = queue.pop(0)
levels.append((element, level))
if level == max_level:
continue
if element in adj_list:
for neighbor in adj_list[element]:
queue.append(neighbor[0])
level += 1
return max_memory, levels
max_memory, levels = level_order_queue_size('A', 5)
max_memory, levels[50:60], len(levels)
(15800, [('H', 3), ('I', 3), ('D', 3), ('B', 3), ('B', 3), ('A', 3), ('B', 3), ('F', 3), ('I', 3), ('G', 3)], 523)
sys.getsizeof(('A', 4))
64
sys.getsizeof(None)
16- Monitoramos o tamanho máximo da fila a qualquer momento quando consideramos a soma dos tamanhos de cada elemento contido na fila.
- De acordo com a documentação do Python,
sys.getsizeofretorna o ponteiro do objeto, ou tamanho, da referência em bytes. Assim, economizamos praticamente 4.4Kb de espaço(20224 — 15800 bytes)quando alteramos o algoritmo original do percurso em nível para usarNone. Esta é apenas a economia de memória desse exemplo aleatório que usamos, e descemos apenas até o 5° nível do percurso. - O último método economiza apenas 16 bytes em relação ao método com
None. Isso acontece porque apenas eliminamos os 4 objetosNoneque estavam sendo usados para marcar os 4 níveis (com exceção do primeiro) que foram processados. Cada ponteiro (ponteiro para um objeto) tem um tamanho de 4 bytes no Python rodando em um ambiente de 32 bits.
Agora que temos todas essas rotas interessantes de múltiplos caminhos, partindo de nossa origem a nosso destino, e algoritmos de percurso em nível altamente eficientes para resolver esse problema, podemos analisar um problema mais lucrativo para resolver usando nosso BFS.
Qual é a rota de voo mais barata, partindo da minha origem até um determinado destino? Eis ai algo capaz de despertar o interesse de todos imediatamente. Quero dizer, quem não quer economizar dinheiro?
Caminho mínimo de uma determinada origem a um destino
Não há muita descrição a ser dada para o enunciado do problema. Precisamos apenas encontrar o caminho mínimo e deixar o usuário final satisfeito.
Algoritmicamente, dado um grafo direcionado ponderado, precisamos encontrar o caminho mínimo da origem ao destino. O mais curto ou o mais barato seriam a mesma coisa do ponto de vista do algoritmo.
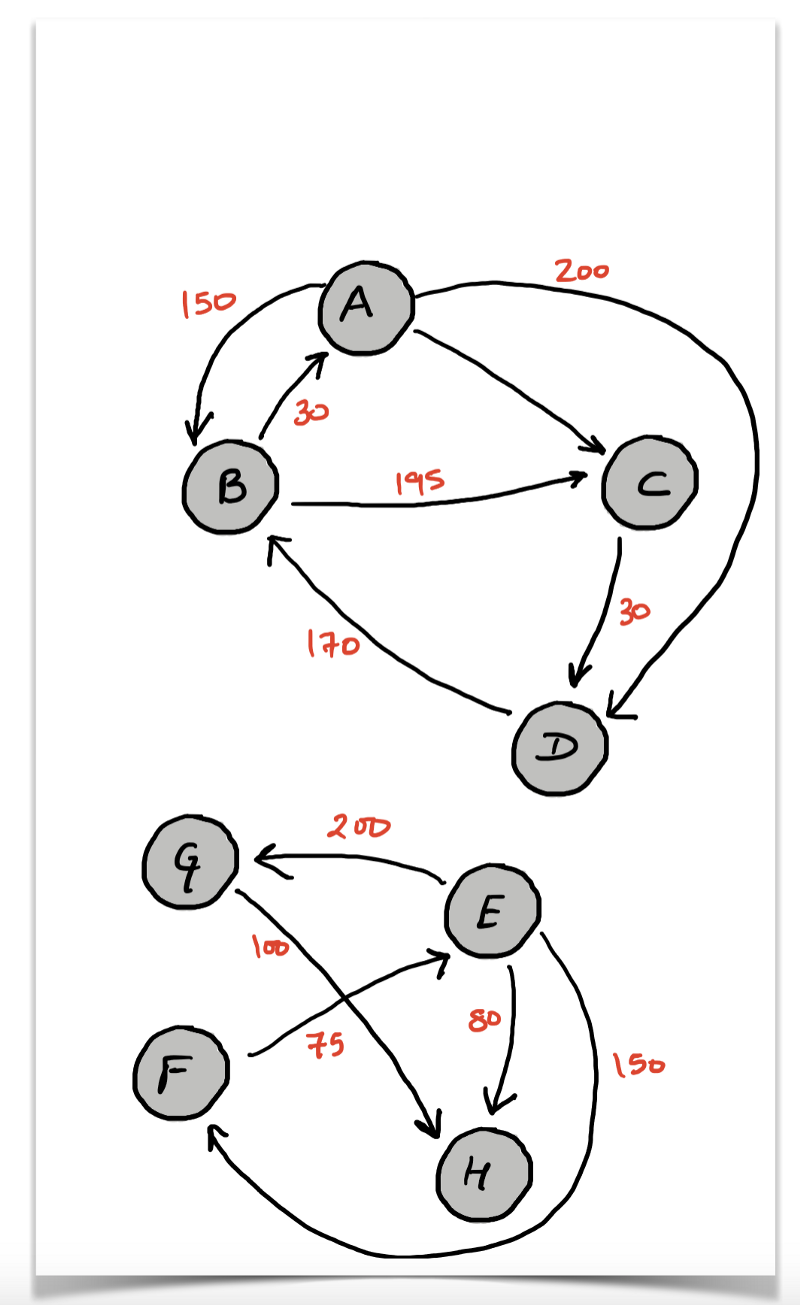
Não vamos descrever uma possível solução BFS para esse problema porque por ela o problema é intratável. Vejamos o grafo abaixo para entender por que esse é o caso.
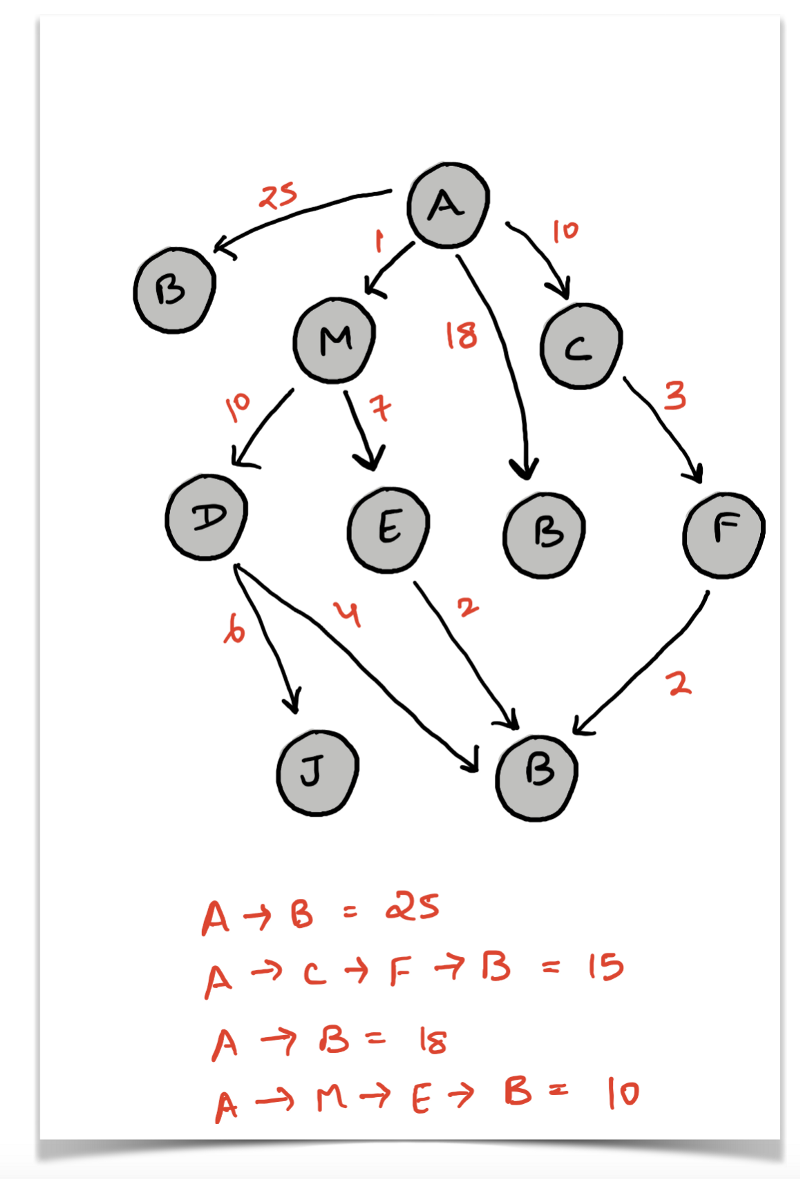
Dizemos que o BFS é o algoritmo a ser usado se quisermos encontrar o caminho mínimo em um grafo não direcionado e não ponderado (texto em inglês). O princípio do BFS é que, na primeira vez que um nó é descoberto durante o percurso, a distância entre ele e o ponto de partida se torna o caminho mínimo.
O mesmo não pode ser dito de um grafo ponderado. Considere o grafo acima. Se, por exemplo, tivéssemos que encontrar o caminho mínimo do nó A ao B numa versão não direcionada desse grafo, então o caminho mínimo seria a aresta que liga A a B. Assim, o caminho mínimo teria tamanho 1 e o BFS funcionaria com precisão.
Entretanto, estamos lidando com um grafo ponderado. Logo, a primeira descoberta de um nó durante o percurso não garante o caminho mínimo para esse nó. Por exemplo, no diagrama acima, o nó B seria descoberto logo no início porque é vizinho de A e o custo associado a esse caminho (uma aresta, nesse caso) seria 25 . Porém, esse não é o caminho mínimo. O caminho mínimo é A --> M --> E --> B , que tem tamanho 10.
A busca em largura não tem como saber se a descoberta de um nó em particular vai nos fornecer o caminho mínimo para esse nó. Portanto, a única maneira possível de o BFS (ou DFS) encontrar o caminho mínimo em um grafo ponderado é varrendo o grafo inteiro e ir registrando a distância mínima da origem até o vértice destino.
Essa solução não é viável para uma rede enorme como a nossa rede aérea, que provavelmente teria milhares de nós.
Não entraremos em detalhes sobre como podemos lidar com isso. Está fora do escopo deste artigo.
O que você faria se eu dissesse que o BFS é o algoritmo certo para encontrar o caminho mínimo em um grafo ponderado sob uma pequena condição?
Caminhos mínimos com restrições
Como o grafo que teríamos para a rede aérea é enorme, sabemos que explorá-lo completamente não é uma possibilidade plausível.
Considere o problema dos caminhos mínimos a partir da perspectiva de um cliente. Quando ele quer reservar um voo, estas são as opções que ele idealmente considera:
- O voo não deve ser muito longo
- Deve caber no orçamento (muito importante)
- Pode ter algumas paradas, mas não mais do que
K, ondeKpode variar dependendo do cliente. - Por fim, temos as preferências pessoais que envolvem coisas como acesso a lounges, qualidade da comida, locais de escala e espaço médio para as pernas.
O ponto principal a ser considerado aqui é o terceiro: pode ter algumas paradas, mas não mais do que K, onde K pode variar dependendo do cliente.
O cliente quer a rota de voo mais barata, mas também não quer, digamos, 20 paradas entre seu ponto de partida e seu destino. O cliente pode concordar com um máximo de 3 paradas ou, em casos extremos, talvez até 4, mas não mais do que isso.
Gostaríamos de ter um programa que descobrisse a rota de voo mais barata com no máximo K paradas para uma determinada origem e destino.
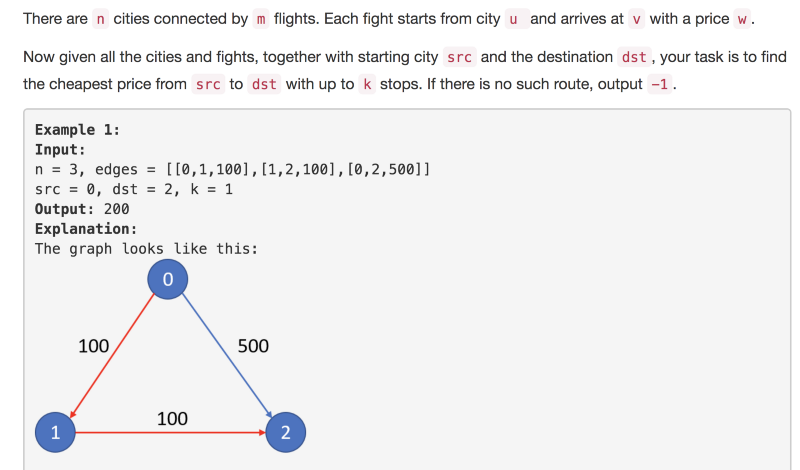
Essa questão do LeetCode foi a principal motivação para que eu escrevesse este artigo. Recomendo fortemente que você analise a questão ao menos uma vez e não confie somente no print que está acima.
"Por que o BFS funcionaria aqui?", alguém poderia perguntar. "Esse também é um grafo ponderado e o motivo pelo qual o BFS não funciona nele. Assim como discutimos na seção anterior, o conceito deveria ser o mesmo." NÃO!
O número de níveis alcançados pela busca é limitado pelo valor de K em questão, descrição fornecida no início da seção. Portanto, essencialmente, estaríamos buscando o caminho mínimo, mas não precisaríamos varrer o grafo inteiro. Vamos apenas até o nível K.
Em um cenário real, o valor de K seria menor que 5 para qualquer passageiro mentalmente são 😝.
Vamos analisar o pseudocódigo do algoritmo:
def bfs(source, destination, K):
min_cost = dictionary representing min cost under K stops for each node reachable from source.
set min_cost of source to be 0
Q = queue()
Q.push(source)
stops = 0
while Q is not empty {
size = Q.size
for i in range 1..size {
element = Q.pop()
if element == destination then continue
for neighbor in adjacency list of element {
if stops == K and neighbor != destination then continue
if min_cost of neighbor improves, update and add back to the queue.
}
}
stops ++
}Novamente, trata-se de um percurso em nível, e a abordagem usada aqui é a que faz uso do tamanho da fila em todos os níveis. Vamos dar uma olhada em uma versão comentada do código para resolver esse problema.
from collections import defaultdict
class Solution:
def findCheapestPrice(self, n, flights, src, dst, K):
"""
:type n: int
:type flights: List[List[int]]
:type src: int
:type dst: int
:type K: int
:rtype: int
"""
# Construa a estrutura de lista de adjacência para ser usada na travessia de ordem de nível.
adj_list = defaultdict(list)
for s, d, cost in flights:
adj_list[s].append((d, cost))
# Inicie um dicionário com os valores de custo mínimo como +inf e 0 para o nó de origem.
min_cost = {k: float("inf") for k in range(n)}
min_cost[src] = 0
queue = [src]
stops = 0
# Execute o while enquanto a fila não estiver vazia, ou seja, enquanto não tivermos examinado todos os nós possíveis de acordo com as restrições.
while queue:
size = len(queue)
for _ in range(size):
element = queue.pop(0)
# Quando um elemento é removido da fila, seu custo atual será o custo mínimo até o momento, da origem até aquele elemento.
cost = min_cost[element]
# Não é necessário processar os filhos do nó de destino.
if element == dst:
continue
# Se esse nó tiver vizinhos
if element in adj_list:
for neighbor, direct_flight_cost in adj_list[element]:
# Não é necessário atualizar o custo mínimo se já esgotamos nossas K paradas.
if stops == K and neighbor != dst:
continue
# Se o comprimento do caminho mínimo atual para `neighbor` puder melhorar, melhore e faça a nova fila
if direct_flight_cost + cost < min_cost[neighbor]:
min_cost[neighbor] = direct_flight_cost + cost
queue.append(neighbor)
# Incremente o nível
stops += 1
return -1 if min_cost[dst] == float("inf") else min_cost[dst]Essencialmente, mantemos o controle da distância mínima de cada nó em relação a uma determinada origem. A distância mínima para a origem seria 0 e +inf para todos os outros inicialmente.
Sempre que encontrarmos um nó, checamos se o comprimento mínimo do caminho em questão pode ser melhorado ou não. Se puder ser melhorado, isso significa que encontramos um caminho alternativo da origem até esse vértice que tem um custo menor - uma rota de voo mais barata até esse vértice. Colocamos esse vértice na fila novamente para que os locais e nós acessíveis a partir desse vértice também sejam atualizados (podendo ou não ser).
O ponto chave é esse:
# Não é necessário atualizar o custo mínimo se já esgotamos nossas K paradas.
if stops == K and neighbor != dst: continueAssim, retiramos o nó A representado por element no código e neighbor pode tanto ser um destino como outro nó qualquer. Se já tivermos esgotado nossas K paradas com o element sendo a K-ésima parada, então não devemos processar e atualizar (possivelmente) a distância mínima para o neighbor. Isso violaria nossa condição de K paradas nesse caso.
Como podem ver, resolvi esse problema originalmente usando programação dinâmica e levou cerca de 165ms para executar no site LeetCode. Executei usando BFS e foi megarrápido, levando apenas 45ms para executar. Essa foi motivação o suficiente para escrever este artigo para vocês.
Espero que tenham aproveitado este artigo sobre a busca em largura e algumas de suas aplicações. O foco principal foi mostrar sua aplicação ao problema do caminho mínimo em um grafo ponderado sob algumas condições😃.