All around us data is transferred faster than ever. Sensitive data is also part of our everyday life. To protect that data, we use encryption. When we encrypt data, it changes in some way that renders it useless to the possible viewer, but that can be changed back to its original state when it arrives safely to the meant receiver. These transformations rely heavily on math, and particularly on a field of math called number theory. This text takes us through the basics of cryptography both from a mathematical perspective and as a programming matter.
Ciphers Yesterday and Today
For as long as writing has existed, the concept of encryption has lived and developed alongside the plain text writing. The idea of rendering text seemingly incomprehensible for purposes of guarding a secret has been central especially in military use and politics. The word cipher originates from the medieval times, from words such as the latin cifra and Arabic صفر (sifr), which means “zero”. There are numerous theories on why zero would have been used to describe encryption, including that the concept of zero was not part of the roman number system and seen as a mystery among numbers. One of the oldest and most widely known ciphers used in military context is Caesars cipher, also known as Caesars shift.
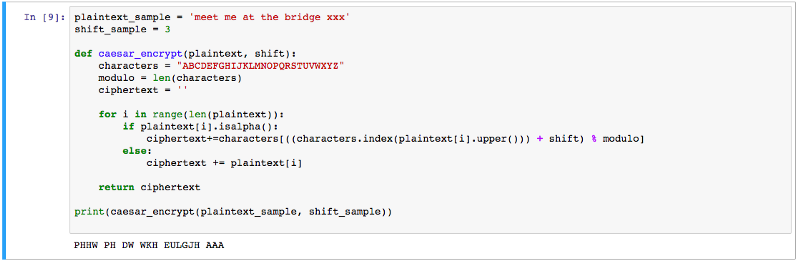
Caesars shift takes one key, which is used to shift each character in the plaintext. This single key is the weakness of the cipher: once the correct shift is figured out, the whole message is revealed. Mathematically, this type of cipher can be written as a problem in modular arithmetic, which works with values wrapped up in a specific range. We’ll discuss this in more depth later.

The way we can solve the plaintext from the encrypted text is by finding the key. In the case of a Caesars cipher of value 3, finding out the key (3) lets us decrypt the whole text in one chunk. The key specifies the output of the encryption algorithm.
Factors and Primes
Perhaps surprisingly, one of the foundational concepts that lays the ground for encryption is that of divisibility. To define what it means, let’s lay down some rules. Firstly, if we have a and b that are integers and a is not 0, a divides b if there is such an integer k that satisfies the following statement.
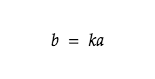
In case we find an integer which is larger than 1 and that does not have other positive factors than 1 and itself, we call it a prime. Integers larger than one which are not primes are known as composite numbers, due to their composed nature. For example, 4 is larger than 1 and it has a factor 2. Hence, it is a composite. On the other hand, 3 is an integer larger than one, but it does not have any other positive factors than 1 and itself. It is a prime. Other small primes are 2, 5, 7, 11 and 13.
According to the fundamental theorem of arithmetic, every integer larger than 1 can be written as an unique product of primes. This is good news for cryptographers, since they love working with primes. Why would that be? Well, one of the most straightforward reasons is that prime factorisation of large numbers takes up a lot of time. Many well known encryption systems such as RSA is fully based on this fact. The principal it works on is that there exists a public key (a product of two large primes) which is used to encrypt the message, and a secret key (containing those primes) which is used to decrypt the message. These primes are usually around 300 digits long.
A Matter of Congruence
Modularity is one of the foundational pillars of cryptography. Let’s approach this concept first from a perspective of division. What happens if we have 5 small candies and three students? Each student gets a candy, and 2 remain. This can be described as the following.

Can you find the other amounts of candies which leave 2 as a remainder when divided to the 3 students? The next amount would be 8, since each student would get two candies and again 2 would be left over. This can be described using congruence. 8 and 5 are congruent is modulo 3, meaning that they leave the same remainder when divided by 3.
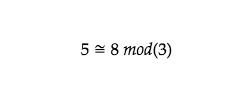
In the example of Caesars shift, we use an alphabet that consists of 26 letters. We only work with those 26 values. After ‘Z’, we go back to ‘A’. This is modularity in practice. ‘A’ will always be at position 1 in our 26-letter list, so any count of position we get, if we divide it by 26 and the remainder is 1, we know to use ‘A’. This wraps up our numbers into a finite field, in which the largest value is 26. In practice, if my secret message would be ‘ABC’, I would first convert this to the numbers 123. After that, I would apply the shift. In case the key would be 3, the shift would produce 456. After this, I would point the numbers back to their letter representations, which are in the class of modulo 26. The encrypted message becomes ‘DEF’.

You can think of this like a clock. When the arrow has gone around the clock, it ends up where it started. In modular arithmetics, the last integer is followed by the first. Another way to understand this is that the world of a specific modulo, only that amount of values exist. For example in modulo 2, only 2 values exist. In our alphabet, 26 values exist, and so on.
Types of Ciphers
What kind of keys a cipher uses can be used to categorise the cipher into asymmetric and symmetric keys. They differ in the question of which key is used for encryption and decryption. Symmetric ciphers are encrypted and decrypted using the same key (such as Caesars Cipher). Asymmetric key ciphers are decrypted with a different key than they are created with, such as the RSA encryption system which we briefly discussed earlier. This results in a longer time for creating the encryption, but the result is also much more secure.
Another way to categorise ciphers is by their way of operating in streams or blocks. Stream ciphers are symmetric key ciphers that operate on continuous streams of symbols. For example the encryptions used in Bluetooth is a stream cipher. Needless to say, in the age of wireless communication with a need for encryption, stream ciphers have become a vital part of mobile technology.
A Look at Stream Ciphers
Remember that we discussed the concept of modular arithmetic earlier? In short, modular arithmetics are arithmetics in a finite field. Now, let’s take a look at another cipher that works with a finite field of values (also known as a Galois field). This cipher, however, does not always produce the same values given the same input, like shifting does. Its purpose is to produce a stream of keys used to encrypt another stream. Like a snake eating its own tail (a symbol often used for eternity), linear feedback shift registers work by feeding on their own output. They are constructed in a way that makes them endlessly cycle through a pattern of values while outputting that seemingly random pattern. The seed and all the outputted values are binary, meaning they get values 0 or 1. The way new values are created is by using a logical operator, usually exclusive or (XOR).
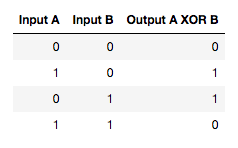
To describe this in a practical way, lets start looking at what we need to create a LFSR. We need a seed, which is a list of ones and zeros. The seed will be what we start shifting. In addition to our seed (or shift register) we have a collection of taps. The taps tell us which parts of the register we use when feeding back into it. Say that we have a seed 001 and two taps, 1 and 3. This means that when we start shifting, the new value will be a combination of the first and third numbers of the seed, 0 and 1. We use an operation called exclusive or to combine the two. 0 xor 1 gives 1. Since we are working with binary values, the feedback from our taps can be expressed as a polynomial in modulo 2.
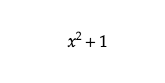
So, if our shift register is 001 and we get a new value, 1, we insert it in the beginning and drop the last number out. Our new shift register state is now 100. We continue this shifting until we notice that our shift register has returned to it’s initial state, 001. Depending on the seed and taps we select, we can get loops of different lengths. A loop is called maximal length if it passes through all possible different combinations before reaching its original state. Since we’re using the binary system, the maximal length of a loop will be 2^n-1. The loop can also end up leaving its original state and getting stuck in a shorter loop within, never returning to its original state. Finding the seeds and taps that lead to a maximal-length cycle is essential. Some of the criterions for finding these taps is that the number of taps must be even and that the taps are setwise co-primes, meaning that they have no common divisor except 1.
Wait, that doesn’t seem so random! Wouldn’t a cycle like that be pretty easy to crack? The thing about shift registers is that they get pretty long, pretty quickly. Say we choose a seed of 20 bits and a tap of two values, 2 and 19. The length of the loop produced is 1 048 575, meaning we would get quite a large amount of seemingly random binary values.
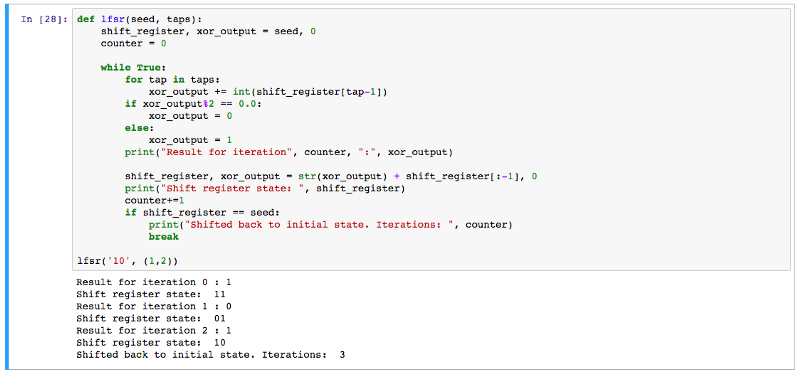
The flavour of LFSR we have briefly gone through is called Fibonacci LFSR. There are also other variations, in which the way the register is shifted differs. They all work to produce a pseudorandom stream of bits used to encrypt streams. The range of applications for this type of encryption ranges from bluetooth to GSM (cellphone communication) standards.
In Conclusion
As a programmer, learning about the concept of modular arithmetics and division opens new ways in thinking about everyday coding problems. However, in security-critical projects using ready-made systems and standards for encryption is always recommended, since specialists in the field of cryptography probably find a safer and more effective solution than an enthusiastic hobbyist.
Sources:
Algebraic Structures in Cryptography by V. Niemi

