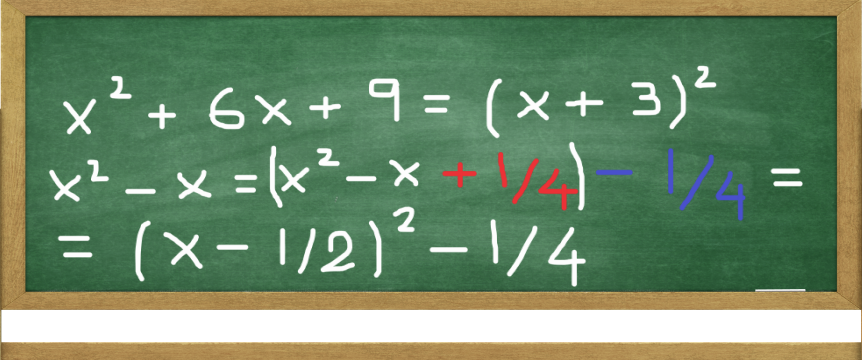Consider the following quadratic equation: x2 = 9. If asked to solve it, we would naturally take the square root of 9 and end up with 3 and -3. But what if simple square root methods won't do? What if the equation includes x raised to the first power and cannot be easily factored?
Fortunately, there is a method for completing the square. As as result, a quadratic equation can be solved by taking the square root. Let's explore this step by step together.
Say we are given the following equation:
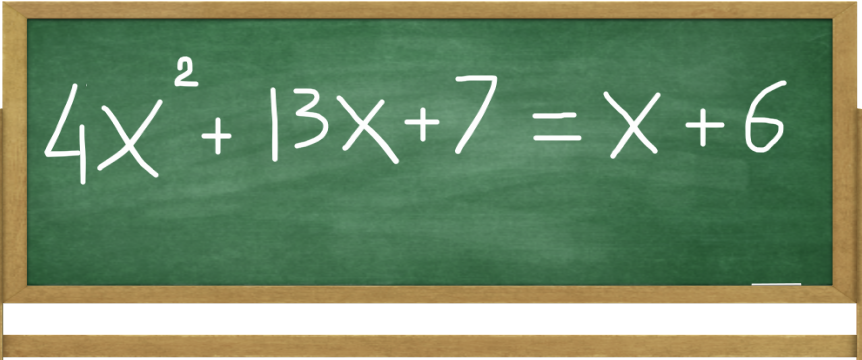
EXAMPLE 1: Completing the square
STEP 1: Separate The Variable Terms From The Constant Term
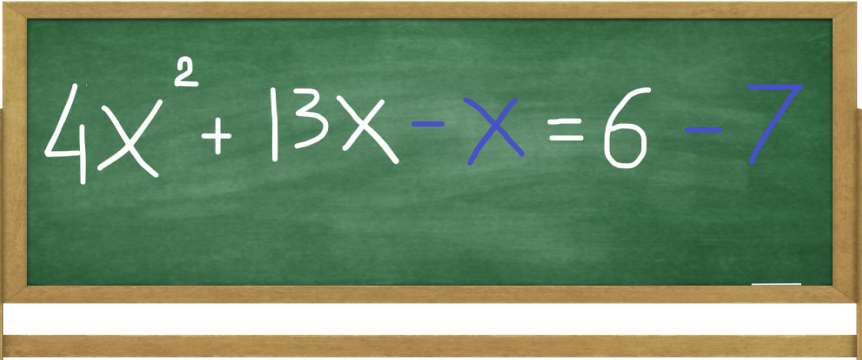
Let's simplify our equation. First, separate the terms that include variables from the constant terms. Next, subtract x from 13x (result is 12x) and subtract 7 from 6 (result is -1).
STEP 2: Make Sure The Coefficient Of X Squared Is Equal To 1
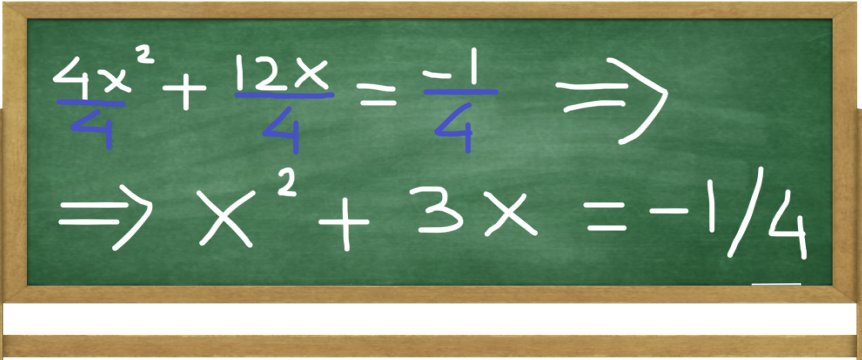
The method of completing the square works a lot easier when the coefficient of x2 equals 1. The coefficient in our case equals 4. Dividing 4 into each member results in x2 + 3x = - 1/4.
STEP 3: Complete The Square
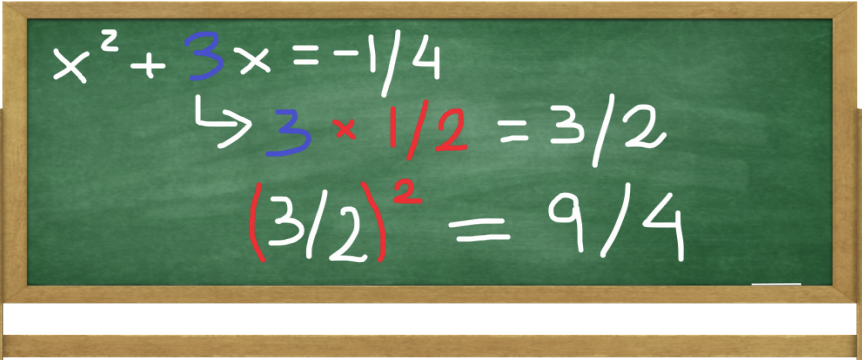
First we need to find the constant term of our complete square. The coefficient of x, which equals 3 is divided by 2 and squared, giving us 9/4.
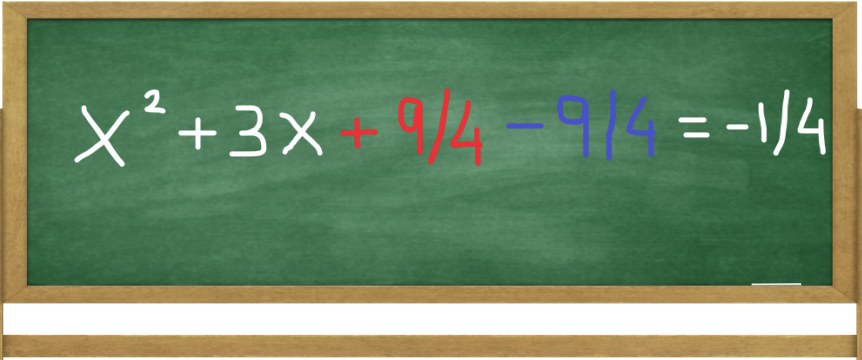
Then we add and subtract 9/4 as shown above. Doing so does not affect our equation (9/4 - 9/4 = 0), but gives us an expression for the complete square x2 + 3x + 9/4.
STEP 4: Factor The Expression X squared + 3X + 9/4
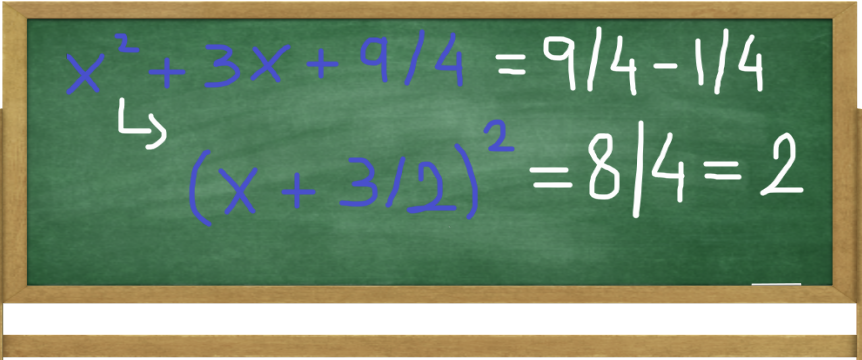
Let's now remember a more general (x + a)2 = x2 + 2ax + a2 and use it in the current example. Substituting our numbers gives us: x2 + 3x + 9/4 = x2 + 2*(3/2)*x + (3/2)2 = (x + 3/2)2.
STEP 5: Take The Square Root
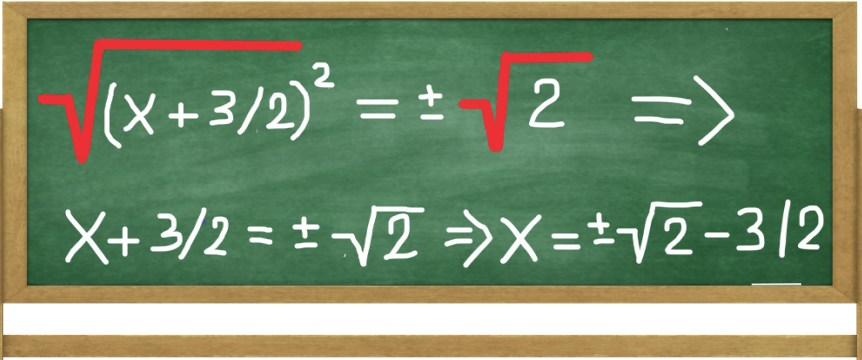
Finally, taking the square root from both sides gives us √(x + 3/2)2 = ±√2. Or simply x + 3/2 = ±√2. We conclude this by solving for x: X1= √2 - 3/2 and X2 = - √2 - 3/2.
EXAMPLE 2: Let's Solve One More
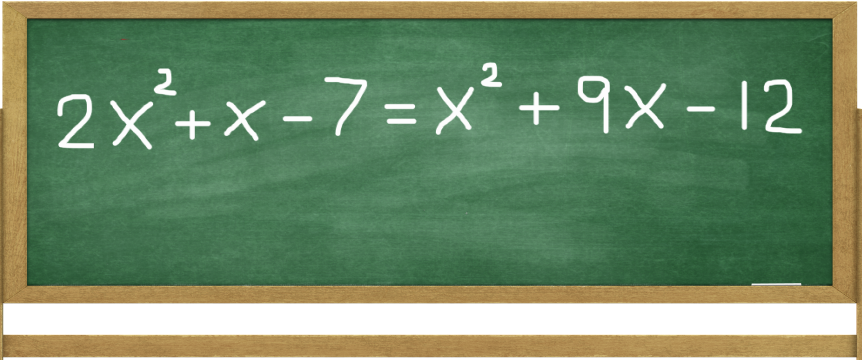
STEP 1: Separate The Variable Terms From The Constant Term
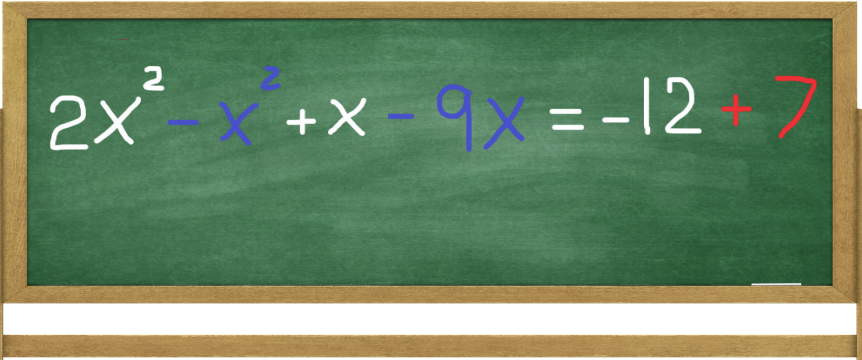
Simplify by separating the terms with variables from constant terms. Then perform subtraction and addition on both sides of the equation.
STEP 2: Make Sure The Coefficient Of x squared Is Equal To 1
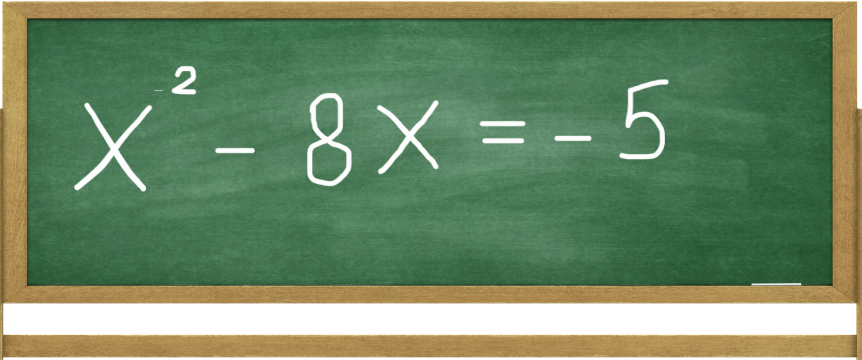
Here, the coefficient of X2 already equals 1, so no further action needed.
STEP 3: Complete The Square
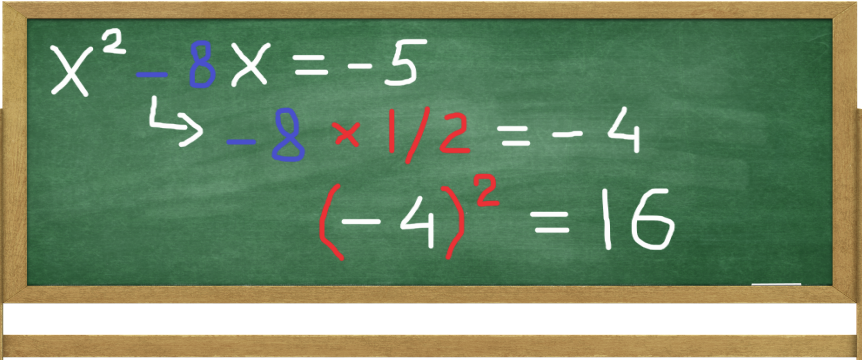
As in previous example, we find the constant term of our complete square. The coefficient of x, which equals -8 is divided by 2 and squared, giving us 16.
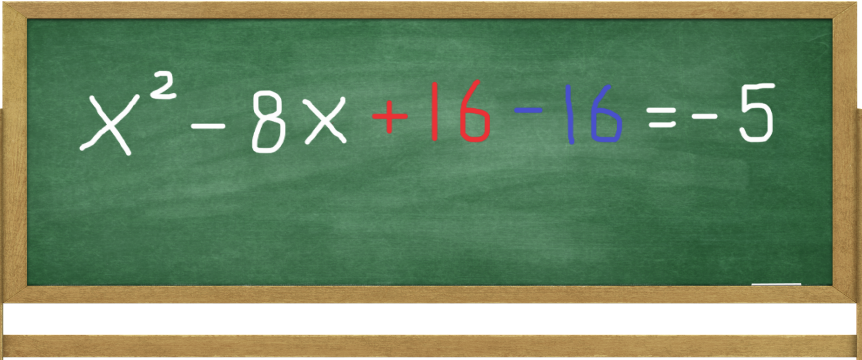
We add and subtract 16 and can see that x2 - 8x + 16 gives us a complete square.
STEP 4: Factor The Expression X squared - 8X + 16
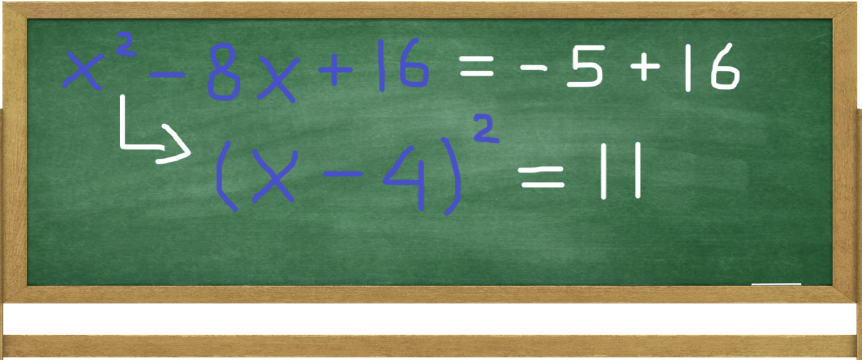
Since the constant term -8 is with the minus sign, we use this general form: (x - a)2 = x2 - 2ax + a2. Using our numbers gives us: x2 - 8x + 16 = x2 - 2*(4)*x + (4)2 = (x - 4)2.
STEP 5: Take The Square Root
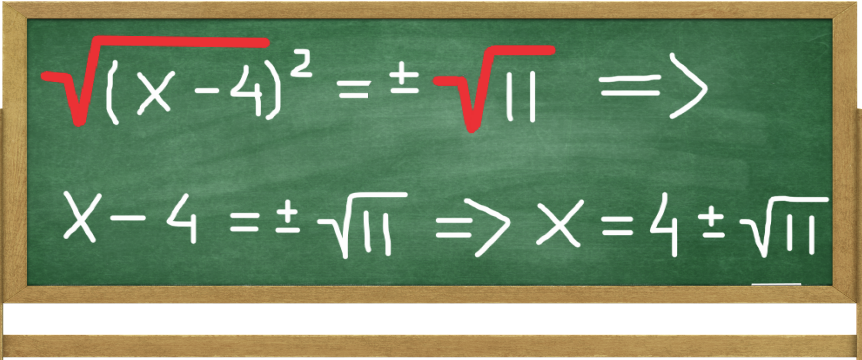
Finally, taking the square root from both sides gives us √(x - 4)2 = ±√11. Or simply x - 4 = ±√11. We conclude this by solving for x: X1 = 4 + √11 and X2 = 4 - √11
And there you have it!