by Pavel Zaytsev
How to write composable functions and correct programs
An overview with monads and Kleisli arrows

A few words on the traditions ?
If you have not written about monads are you even a programmer?
It is a well-known fact that any respectable programmer who blogs about tech must at least once in their life write a tutorial on monads. Most of the times it starts from functors and builds all the way up. The difficult comparisons are drawn here and there with the short snippets of code sprinkled around to demonstrate a couple of applications — all seem completely orthogonal, of course.
The problem is that there is a gigantic conceptual gap between “What is a monad?” and “How is a monad used in programming?”
The main reason for this gap is that people don’t usually think of their programs in such a way that they would need a monad in the first place. If you come from the imperative background — and most of us do — even when you finally go functional, it usually takes a while to see the entire picture and understand the correct way of doing things. We often preach referential transparency and purity. We often have a general idea of what these things mean separately, but it takes some time to piece them together in one coherent concept.
This article is not about monads but instead about writing composable functions and correct programs. The monads appear as the by-product of this goal. The following discussion also, hopefully, will facilitate bridging the aforementioned conceptual gap.
It’s all about that composition ?
In programming, the interesting and important problems are usually too complex too to deal with as a whole. Programmers break them up into smaller comprehensible pieces that they solve one-by-one and then bring the solutions to these subproblems into a clear picture. There are many ways of doing it, but there can be clearly defined two schools of thought — declarative and imperative approaches.
The imperative approach views a program as a sequence of computations in time, and the unit of a program is a statement. A statement does something. For example, it can print output to a console, assign a value to a variable, or compute a result.
The declarative approach is global. It cares only about the initial and final state of the system, and a unit of a program is an expression. The expression always evaluates to a value. In general, it’s harder to reason about a statement rather than about an expression because a statement is far too broad and unbounded, while an expression always deterministically evaluates to the same value for all the programs it can potentially appear in.
If you are a functional programmer and you follow a declarative paradigm, you see a program as a composition of functions, and functions are just the expressions. You can think of a composition as just a fusion of two or more functions into one.
If you have a function f that takes an argument of type A and it returns a result of type B and another function g that takes an argument of type B, and it returns a result of type C, you can compose them by passing a result of f to g. What you get is a new function that accepts an argument of type A and produces the result of type C. Do a couple of these, and you get a working program. This is similar to deductive reasoning, which is just a composition of logical steps, that follow from premises to the conclusions.
The problem is that in real programming it’s not so simple, and many functions do not evaluate to the same value all the time even if their arguments do. These functions do network calls, they read from files and databases, they write to them, they process a lot of different data, they print to a console, etc. Functions become context-dependent, and the more context-dependent they are, the more difficult it is to compose them. So if you have to deal with functions where each one of them introduces some of this complexity here and there, you better find a way to compose them.
The ever-lasting problem ?
As I have already mentioned, writing useful code entails dealing with the chaos of the outside world — a problem of handling effects and state. By effect, I mean an effect on the outside world, like writing to a database or printing to a console. Even a simple beaten-to-death HelloWorld program produces an effect.
Many situations are traditionally solved by abandoning the purity of functions, including but not limited to:
- computations that access/modify a state outside of the context of a program.
- computations that may fail or never terminate
- computations whose result might be only known sometime in the future, aka asynchronous computations
- console input and output
As you can imagine, the functions that behave like this are not so easy to compose. Let’s say a function, given some username in the form of an input string, reads from a file, finds the given user, and then passes their last name to the next function for later processing. How do you represent a function like that? String => String? But that would not be entirely correct, as you do get a string and you do return one, but you also do something else in between and it depends on the context — a file system and a file.
In functional programming, we usually encode this information in the function’s return type. We place the result of a computation in a box, so to speak, and our function turns from A =>; B to A => Box[B].
Whatever happens inside this box is implementation-specific. But the definition of a function now describes what it does and allows to handle the function's behavior and compose it, much better.
Let’s look at the situations above and try to come up with a box for every one of them.
Box all the things ?
Disclaimer: In this article, I will be using Scala to express my ideas, as it’s arguably one of the mainstream functional programming languages out there. But the same concepts can be easily translated into any functional programming language with a strong static type system and type constructors (like Haskell and OCaml).
A function that reads but does not modify the external state can be thought of as a function that also accepts this external state as an argument and, given some input parameter, produces a result. An example is reading from a database or config file.
We also supply a run function to materialize a reader and compute a result. The classic use case would be to:
- provide a configuration file
- stack the readers to set up an application
- execute the
runfunction in the end on the instance of the config file.
In the OOP world, a similar approach goes by Dependency Injection.
Functions that carry along the state of a computation accept two arguments — a regular one, that participates in the actual computation, and the state that will be propagated all the way through the composition.
We supply a run function that yields the result which a current writer holds. A typical use case of Writer is to propagate messages and errors during the program execution, and extracts the log alongside the final result. Another use case would be to record the sequences of steps in a multi-threaded environment. Since the result of a computation is tied to a particular log, the messages don’t get intertwined.
A function that never terminates (for example a long running process) is lifted to a bottom type of Nothing. If you expect that your computation might either return a value or run forever, you can model it as a disjoint union of a result type and Nothing. An example would be a stream consumer that processes data indefinitely until some event makes it yield.
A function that might fail can be modeled as a partial function — the one that’s not defined for some values. So we do just that — for some cases return nothing and, for others, an actual value. If you want the information regarding the failure and to interop with Java APIs that throw exceptions, you can carry the information of an error with you in the disjoint union.
Asynchronous computations do not execute on the current call-stack or a main flow of the program. They can be modeled as a function that accepts a handler, or callback. When this handler eventually is called — for example by some other thread or a web server — the result is produced.
ExecutionContext manages the details of the asynchronous execution. On JVM it is a thread-pool, but it does not have to be threads that deal with asynchrony. Function run takes it implicitly because callbacks need to be called asynchronously. Every function that calls run needs to have an implicit ExecutionContext in its signature as well. ExecutionContext also makes recursive asynchronous calls stack-safe because you introduce an asynchronous boundary every time you call a function. As I mentioned earlier, asynchronous computations do not execute on the same call-stack. Pretty neat.
Console input can be modeled as a two-phase process. In the first phase we describe the computation and a result that a console input might produce. In the second phase, we run or interpret this computation. The data type that holds the outcome of this computation is called IO. So our function takes a singleton and produces the result inside of an IO.
Notice, since I mentioned that we describe the computation first, we pass call-by-name parameters =>; A. They execute only when we need them to.
Console output can be modeled through IO as well, with our run function producing a singleton type of Unit.
So, now what ? ?
We, of course, implemented all the boxes with a type parameter to account for variability in types. We transform, or map, from some stuff to other stuff by supplying a function. A mapping between a category of some things to a category of other things is called a functor.
Functors are cool because they allow us to transform stuff inside, while preserving the structure of the original category, without messing things up. When using a functor, following the functor laws proves that things work as expected. It will get clear later in the article why these laws in particular.
Let’s define a map method that does transformation for each of the derived data types:
Notice that here we have defined a function pure that permits us to lift a pure computation into an asynchronous value.
Cool, now we can map things inside of the boxes. The problem is — it’s not useful because, although we can sequence computations within a functor, we can’t compose functor-producing functions:
F1: A -> Functor[B] ==> F2: A -> Functor[B] ==> F3: A -> Functor[B]Each of F1, F2, and F3 may do something completely different. We need to account for that, we need to compose them. Fortunately, there is an excellent way of doing this.
Oh no, it’s that guy again! ?
Ok, I need to write a function that composes the functions for each of the functors in A => Functor[B]. The mathematical definition of composition is:
If A =>; B and B => C then A => CSo in our case:
If A => Functor[B] and B => Functor[C] then A => Functor[C]Let’s start with a reader. Again, just follow the types:
We defined composition as andThen . We also defined pure , which lifts a value into a functor.
Composition in any category follows two simple laws.
- It is associative:
2. There exists such a function, called identity, that, when composed with any function from left or right, produces that function again:
You can take a pen and a piece of paper and try to draw these two laws. Substituting entities with circles and connections between them as arrows, you can visually prove to yourself that this is the case. Remember functor laws earlier? It’s the same thing. These laws establish the composability in every category.
As programmers, we mostly deal with a category of sets — objects are sets or types, and arrows are functions. Not all mathematical structures need to have an identity, but category certainly does.
Identity, for example, can be used to show whether two objects, “sets,” are isomorphic, or equal. It can also provide guarantees in certain instances as we will see later in the article.

A functor that participates in A => Functor[B] and follows these composition laws, and hence composes for all the objects in the same category is not a burrito. It’s a monad.
Accordingly, the functions that we try to compose are actually A => Monad[B] . A wrapper around them, a category that is naturally associated with a Monad[B], is called a Kleisli category. A => Monad[B] or Kleisli arrows is just a way to compose these sort of functions, nothing more.
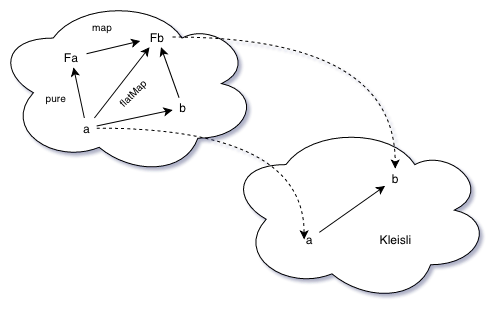
Compose all the things! ?
We replace Java-like andThen with an arrow >==> . This is called a fish operator because it looks like a fish ?. We also define a function flatMap that, given a Monad[A] and A => Monad[B], produces A => Monad[B]. This will make implementing arrows easier:
Monoids
For a writer to be a monad, a second type should be composable too, and it’s composable only if it’s a monoid. Something is a monoid only if it can be associatively combined and has an empty element, which is an identity element.
For example, integers that sum up are a monoid with an identity element of 0. Strings that concat are a monoid with identity element of an empty string. Sets that union are a monoid with an identity element of an empty set. Sets that intersect form a semigroup and not a monoid. Intersecting a non-empty set with an empty one produces an empty set. You see why identity is useful?
Every other monad is easy to implement:
We will go into detail why IO looks like this and have a discussion about Free probably in another article.
When to use which? ?
Kleisli and Monad are two sides of the same coin. Many functional languages support them natively, but for Scala, at least in the current version 2.12.8, you can get them from the libraries like Cats and Scalaz. They have type classes for Kleisli and Monad: Kleisli[F[_], A, B] and Monad[A] respectively.
Monads are better at expressing the sequencing of the computations that happen within some context. In Scala, we do this contextual sequencing usually by utilizing for comprehensions.
Fun fact: If you compose Kleisli arrows for IO monad, you will get a description of your computer program. Your computer program is essentially one gigantic Kleisli arrow, with some input and output of Unit that acts as a description, and a runtime environment that executes this program works as an interpreter.
So every program, by default, has an IO context. If you have a function that produces an error, it creates a context of Option or Either. So every subsequent function should have a signature of A => Option[A] or A => Either[A, B]. Within an IO program it’s A => IO[Option[A]] and A => IO[Either[A, B]]. You decide when to collapse this context or nest it even further. Monad transformers can help with the sequencing of the nested contexts, but that is material for another article.
Asynchronous computations are only sequenced with the help of monads because monads explicitly solve the problems of synchronization and ordering in time. If you use Future combinators, for example, it is within a monadic context.
Kleisli is better when the arrow combinator is more suitable. For example, we can have a bunch of effectful or impure functions, and we can fuse them without wrapping the result into IO. You can also create a bunch of individual programs and combine them into one Kleisli in the end and run if you want, of course.
Reader[A] is better expressed with Kleisli than with monadic compositions because we can easily compose small local Kleisli arrows into a Kleisli arrow that represents our program’s global configuration. The large Kleisli arrow depends on some environment, let’s say a configuration file for production and development. Then we can run this at the very end, and configure the entire app.
This approach mimics the concept of dependency injection. Here we demonstrate KleisliIO, an effectful Kleisli from ZIO that performs a reader functionality to configure the application (error type omitted to save some space):
End ?
Whew, that was a blast. I hope you enjoyed this article and now understand what’s going a little bit better :).
Here are some useful links to learn more about Kleisli and composition: