Artigo original: https://www.freecodecamp.org/news/eulers-method-explained-with-examples/
O método de Euler é um procedimento numérico de primeira ordem para resolver equações diferenciais ordinárias (EDO ou, em inglês, ODE – ordinary differential equations) com um valor inicial fornecido.
O problema do valor inicial geral
Metodologia
O método de Euler usa a fórmula simples,
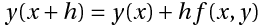
para construir a tangente no ponto x e obter o valor de y(x+h), cuja inclinação é
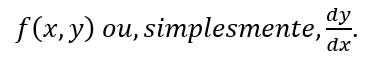
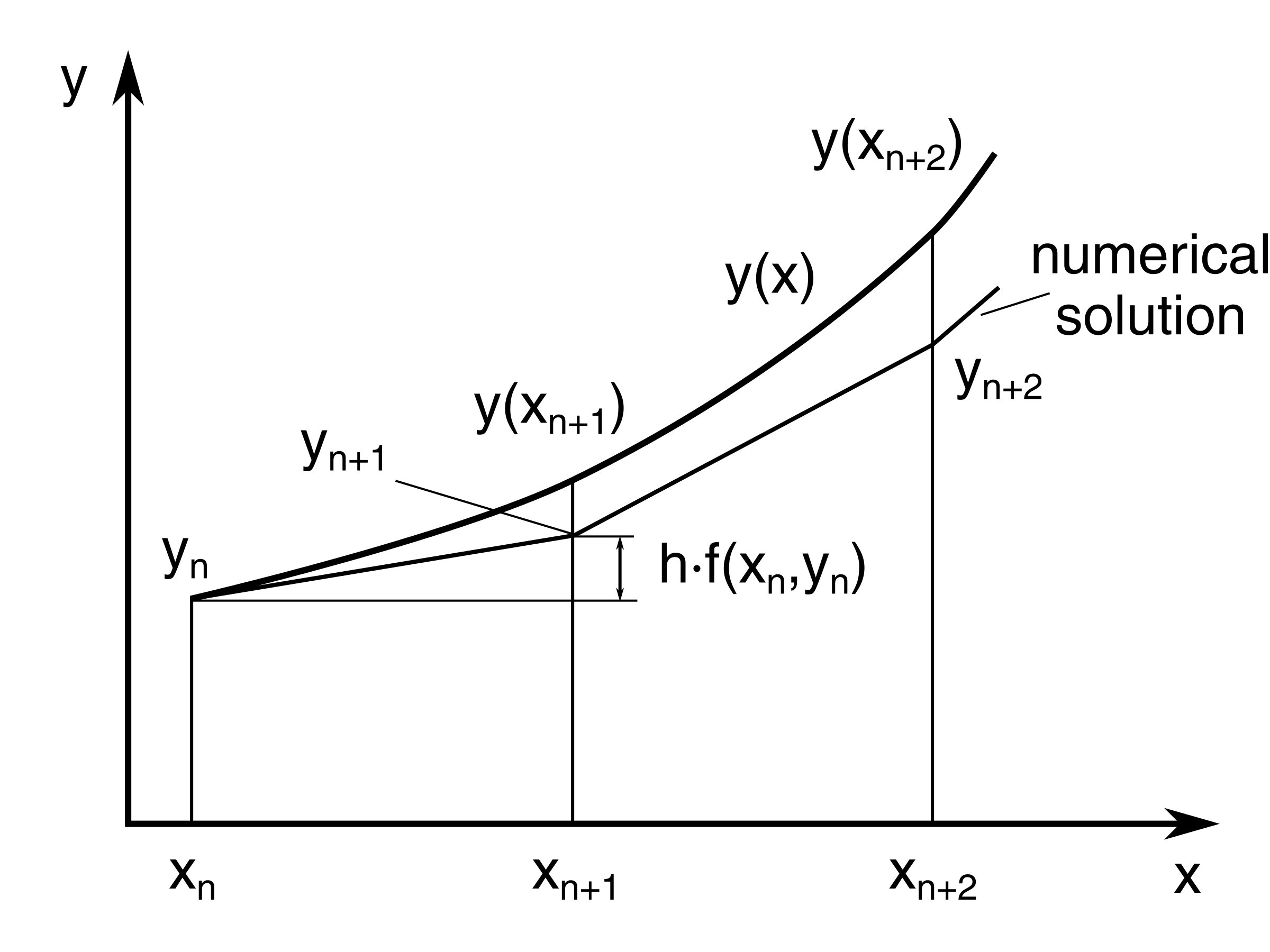
No método de Euler, você pode aproximar a curva da solução pela tangente em cada intervalo (ou seja, por uma sequência de segmentos de linha curtos), em passos de h.
Em geral, se você usar um tamanho de passo menor, a precisão da aproximação aumenta.
Fórmula geral
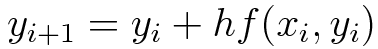

onde:
- y1+1 é o próximo valor de solução estimado;
- y1 é o valor atual;
- h é o intervalo entre os passos;
- f(x1, y1) é o valor da derivada no ponto atual (x1, y1).
Valor da função em qualquer ponto b, dado por y(b)
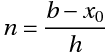
onde:
- n = número de passos
- h = largura do intervalo (tamanho de cada passo)
Pseudocódigo
- defina f(x, y)
- insira x0, y0
- insira h, n
- para j de 0 a (n-1), faça
- yj+1 = yj + hf(xj, yj)
- xj+1 = xj + h
- imprima xj + 1 e yj + 1
5. fim
Exemplo
Encontre y(1), dado que
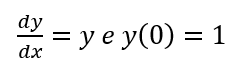
Resolvendo analiticamente, a solução é y = ex e y(1)= 2.71828. (Observação: essa solução analítica é apenas para comparar a precisão.)
Usando o método de Euler, considerando que h = 0.2, 0.1, 0.01, você pode ver os resultados no diagrama abaixo.
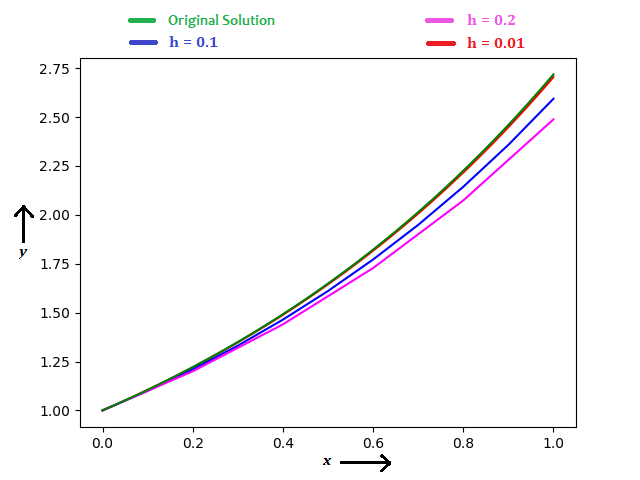
Quando h = 0.2, y(1) = 2.48832 (erro = 8.46 %)
Quando h = 0.1, y(1) = 2.59374 (erro = 4.58 %)
Quando h = 0.01, y(1) = 2.70481 (erro = 0.50 %)
Como é possível observar, a precisão aumenta quando os passos são menores.

