by Nick Gard
I am a front-end engineer and mathematician. I rely on my mathematical training daily in writing code. It’s not statistics or calculus that I use but, rather, my thorough understanding of Boolean logic. Often I have turned a complex combination of ampersands, pipes, exclamation marks, and equals signs into something simpler and much more readable. I’d like to share this knowledge, so I wrote this article. It’s long but I hope it is as beneficial to you as it has been to me. Enjoy!
Truthy & Falsy values in JavaScript
Before studying logical expressions, let’s understand what’s “truthy” in JavaScript. Since JavaScript is loosely typed, it coerces values into booleans in logical expressions. if statements, &&, ||, and ternary conditions all coerce values into booleans. Note that this doesn’t mean that they always return a boolean from the operation.
There are only six falsy values in JavaScript — false, null, undefined, NaN, 0, and "" — and everything else is truthy. This means that [] and {} are both truthy, which tend to trip people up.
The logical operators
In formal logic, only a few operators exist: negation, conjunction, disjunction, implication, and bicondition. Each of these has a JavaScript equivalent: !, &&, ||, if (/* condition */) { /* then consequence */}, and ===, respectively. These operators create all other logical statements.
Truth Tables
First, let’s look at the truth tables for each of our basic operators. A truth table tells us what the truthiness of an expression is based on the truthiness of its parts. Truth tables are important. If two expressions generate the same truth table, then those expressions are equivalent and can replace one another.
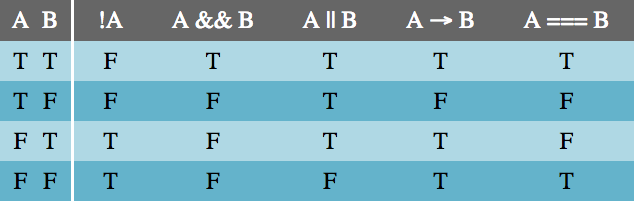
The Negation table is very straightforward. Negation is the only unary logical operator, acting only on a single input. This means that !A || B is not the same as !(A || B). Parentheses act like the grouping notation you’d find in mathematics.
For instance, the first row in the Negation truth table (below) should be read like this: “if statement A is True, then the expression !A is False.”
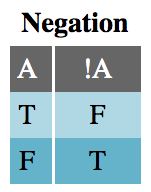
Negating a simple statement is not difficult. The negation of “it is raining” is “it is not raining,” and the negation of JavaScript’s primitive true is, of course, false. However, negating complex statements or expressions is not so simple. What is the negation of “it is always raining” or isFoo && isBar?
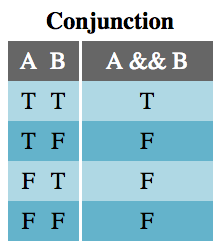
The Conjunction table shows that the expression A && B is true only if both A and B are true. This should be very familiar from writing JavaScript.
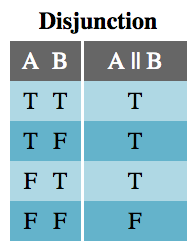
The Disjunction table should also be very familiar. A disjunction (logical OR statement) is true if either or both of A and B are true.
The Implication table is not as familiar. Since A implies B, A being true implies B is true. However, B can be true for reasons other than A, which is why the last two lines of the table are true. The only time implication is false is when A is true and B is false because then A doesn’t imply B.
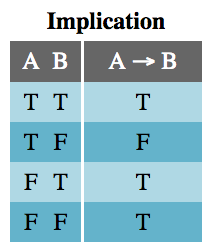
While if statements are used for implications in JavaScript, not all ifstatements work this way. Usually, we use if as a flow control, not as a truthiness check where the consequence also matters in the check. Here is the archetypical implication if statement:
function implication(A, B) { if (A) { return B; } else { /* if A is false, the implication is true */ return true; }}Don’t worry that this is somewhat awkward. There are easier ways to code implications. Because of this awkwardness, though, I will continue to use →as the symbol for implications throughout this article.
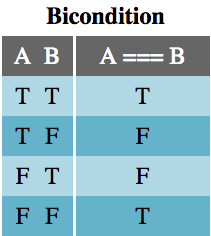
The Bicondition operator, sometimes called if-and-only-if (IFF), evaluates to true only if the two operands, A and B, share the same truthiness value. Because of how JavaScript handles comparisons, the use of === for logical purposes should only be used on operands cast to booleans. That is, instead of A === B, we should use !!A === !!B.
Caveats
There are two big caveats to treating JavaScript code like propositional logic: short circuiting and order of operations.
Short circuiting is something that JavaScript engines do to save time. Something that will not change the output of the whole expression is not evaluated. The function doSomething() in the following examples is never called because, no matter what it returned, the outcome of the logical expression wouldn’t change:
// doSomething() is never calledfalse && doSomething();true || doSomething();Recall that conjunctions (&&) are true only if both statements are true, and disjunctions (||) are false only if both statements are false. In each of these cases, after reading the first value, no more calculations need to be done to evaluate the logical outcome of the expressions.
Because of this feature, JavaScript sometimes breaks logical commutativity. Logically A && B is equivalent to B && A, but you would break your program if you commuted window && window.mightNotExist into window.mightNotExist && window. That’s not to say that the truthiness of a commuted expression is any different, just that JavaScript may throw an error trying to parse it.
The order of operations in JavaScript caught me by surprise because I was not taught that formal logic had an order of operations, other than by grouping and left-to-right. It turns out that many programming languages consider &&to have a higher precedence than ||. This means that && is grouped (not evaluated) first, left-to-right, and then || is grouped left-to-right. This means that A || B && C is not evaluated the same way as (A || B) && C, but rather as A || (B && C).
true || false && false; // evaluates to true(true || false) && false; // evaluates to falseFortunately, grouping, (), holds the topmost precedence in JavaScript. We can avoid surprises and ambiguity by manually associating the statements we want evaluated together into discrete expressions. This is why many code linters prohibit having both && and || within the same group.
Calculating compound truth tables
Now that the truthiness of simple statements is known, the truthiness of more complex expressions can be calculated.
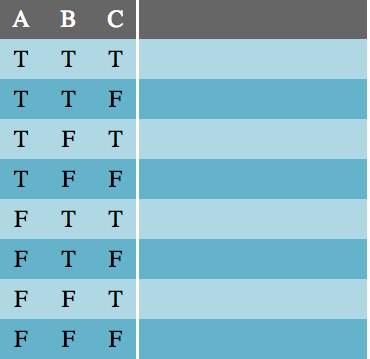
To begin, count the number of variables in the expression and write a truth table that has 2ⁿ rows.
Next, create a column for each of the variables and fill them with every possible combination of true/false values. I recommend filling the first half of the first column with T and the second half with F, then quartering the next column and so on until it looks like this:
Then write the expression down and solve it in layers, from the innermost groups outward for each combination of truth values:
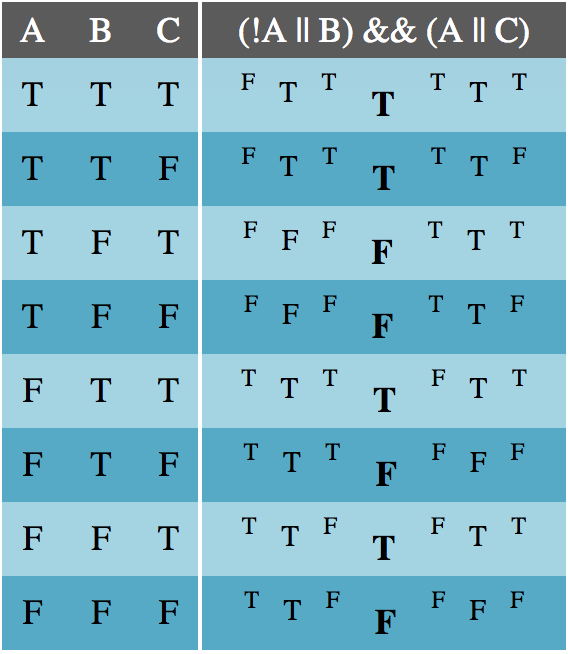
As stated above, expressions which produce the same truth table can be substituted for each other.
Rules of replacements
Now I’ll cover several examples of rules of replacements that I often use. No truth tables are included below, but you can construct them yourself to prove that these rules are correct.
Double negation
Logically, A and !!A are equivalent. You can always remove a double negation or add a double negation to an expression without changing its truthiness. Adding a double-negation comes in handy when you want to negate part of a complex expression. The one caveat here is that in JavaScript !! also acts to coerce a value into a boolean, which may be an unwanted side-effect.
A === !!ACommutation
Any disjunction (||), conjunction (&&), or bicondition (===) can swap the order of its parts. The following pairs are logically equivalent, but may change the program’s computation because of short-circuiting.
(A || B) === (B || A)(A && B) === (B && A)(A === B) === (B === A)
Association
Disjunctions and conjunctions are binary operations, meaning they only operate on two inputs. While they can be coded in longer chains — A || B || C || D — they are implicitly associated from left to right — ((A || B) || C) || D. The rule of association states that the order in which these groupings occur make no difference to the logical outcome.
((A || B) || C) === (A || (B || C))((A && B) && C) === (A && (B && C))
Distribution
Association does not work across both conjunctions and disjunctions. That is, (A && (B || C)) !== ((A && B) || C). In order to disassociate B and C in the previous example, you must distribute the conjunction — (A && B) || (A && C). This process also works in reverse. If you find a compound expression with a repeated disjunction or conjunction, you can un-distribute it, akin to factoring out a common factor in an algebraic expression.
(A && (B || C)) === ((A && B) || (A && C))(A || (B && C)) === ((A || B) && (A || C))
Another common occurrence of distribution is double-distribution (similar to FOIL in algebra):
1. ((A || B) && (C || D)) === ((A || B) && C) || ((A || B) && D)
2. ((A || B) && C) || ((A || B) && D) ===((A && C) || B && C)) || ((A && D) || (B && D))
(A || B) && (C || D) === (A && C) || (B && C) || (A && D) || (B && D)(A && B) ||(C && D) === (A || C) && (B || C) && (A || D) && (B || D)
Material Implication
Implication expressions (A → B) typically get translated into code as if (A) { B } but that is not very useful if a compound expression has several implications in it. You would end up with nested if statements — a code smell. Instead, I often use the material implication rule of replacement, which says that A → B means either A is false or B is true.
(A → B) === (!A || B)Tautology & Contradiction
Sometimes during the course of manipulating compound logical expressions, you’ll end up with a simple conjunction or disjunction that only involves one variable and its negation or a boolean literal. In those cases, the expression is either always true (a tautology) or always false (a contradiction) and can be replaced with the boolean literal in code.
(A || !A) === true(A || true) === true(A && !A) === false(A && false) === false
Related to these equivalencies are the disjunction and conjunction with the other boolean literal. These can be simplified to just the truthiness of the variable.
(A || false) === A(A && true) === A
Transposition
When manipulating an implication (A → B), a common mistake people make is to assume that negating the first part, A, implies the second part, B, is also negated — !A → !B. This is called the converse of the implication and it is not necessarily true. That is, having the original implication does not tell us if the converse is true because A is not a necessary condition of B. (If the converse is also true — for independent reasons — then A and B are biconditional.)
What we can know from the original implication, though, is that the contrapositive is true. Since B is a necessary condition for A (recall from the truth table for implication that if B is true, A must also be true), we can claim that !B → !A.
(A → B) === (!B → !A)Material Equivalence
The name biconditional comes from the fact that it represents two conditional (implication) statements: A === B means that A → B and B → A. The truth values of A and B are locked into each other. This gives us the first material equivalence rule:
(A === B) === ((A → B) && (B → A))Using material implication, double-distribution, contradiction, and commutation, we can manipulate this new expression into something easier to code:
1. ((A → B) && (B → A)) === ((!A || B) && (!B || A))
2. ((!A || B) && (!B || A)) === ((!A && !B) || (B && !B)) || ((!A && A) || (B && A))
3. ((!A && !B) || (B && !B)) || ((!A && A) || (B && A)) === ((!A && !B) || (B && A))
4. ((!A && !B) || (B && A)) === ((A && B) || (!A && !B))
(A === B) === ((A && B) || (!A && !B))Exportation
Nested if statements, especially if there are no else parts, are a code smell. A simple nested if statement can be reduced into a single statement where the conditional is a conjunction of the two previous conditions:
if (A) { if (B) { C }}// is equivalent toif (A && B) { C}(A → (B → C)) === ((A && B) → C)DeMorgan’s Laws
DeMorgan’s Laws are essential to working with logical statements. They tell how to distribute a negation across a conjunction or disjunction. Consider the expression !(A || B). DeMorgan’s Laws say that when negating a disjunction or conjunction, negate each statement and change the && to ||or vice versa. Thus !(A || B) is the same as !A && !B. Similarly, !(A && B)is equivalent to !A || !B.
!(A || B) === !A && !B!(A && B) === !A || !B
Ternary (If-Then-Else)
Ternary statements (A ? B : C) occur regularly in programming, but they’re not quite implications. The translation from a ternary to formal logic is actually a conjunction of two implications, A → B and !A → C, which we can write as: (!A || B) && (A || C), using material implication.
(A ? B : C) === (!A || B) && (A || C)XOR (Exclusive Or)
Exclusive Or, often abbreviated xor, means, “one or the other, but not both.” This differs from the normal or operator only in that both values cannot be true. This is often what we mean when we use “or” in plain English. JavaScript doesn’t have a native xor operator, so how would we represent this?
1. “A or B, but not both A and B”
2. (A || B) && !(A && B) direct translation
3. (A || B) && (!A || !B) DeMorgan’s Laws
4. (!A || !B) && (A || B) commutativity
5. A ? !B : B if-then-else definition
A ? !B : B is exclusive or (xor) in JavaScriptAlternatively,
1. “A or B, but not both A and B”
2. (A || B) && !(A && B) direct translation
3. (A || B) && (!A || !B) DeMorgan’s Laws
4. (A && !A) || (A && !B) || (B && !A) || (B && !B) double-distribution
5. (A && !B) || (B && !A) contradiction replacement
6. A === !B or A !== B material equivalence
A === !BorA !== Bis xor in JavaScript
Set Logic
So far we have been looking at statements about expressions involving two (or a few) values, but now we will turn our attention to sets of values. Much like how logical operators in compound expressions preserve truthiness in predictable ways, predicate functions on sets preserve truthiness in predictable ways.
A predicate function is a function whose input is a value from a set and whose output is a boolean. For the following code examples, I will use an array of numbers for a set and two predicate functions:isOdd = n => n % 2 !== 0; and isEven = n => n % 2 === 0;.
Universal Statements
A universal statement is one that applies to all elements in a set, meaning its predicate function returns true for every element. If the predicate returns false for any one (or more) element, then the universal statement is false. Array.prototype.every takes a predicate function and returns true only if every element of the array returns true for the predicate. It also terminates early (with false) if the predicate returns false, not running the predicate over any more elements of the array, so in practice avoid side-effects in predicates.
As an example, consider the array [2, 4, 6, 8], and the universal statement, “every element of the array is even.” Using isEven and JavaScript’s built-in universal function, we can run [2, 4, 6, 8].every(isEven) and find that this is true.
Array.prototype.every is JavaScript’s Universal StatementExistential Statements
An existential statement makes a specific claim about a set: at least one element in the set returns true for the predicate function. If the predicate returns false for every element in the set, then the existential statement is false.
JavaScript also supplies a built-in existential statement: Array.prototype.some. Similar to every, some will return early (with true) if an element satisfies its predicate. As an example, [1, 3, 5].some(isOdd) will only run one iteration of the predicate isOdd (consuming 1 and returning true) and return true. [1, 3, 5].some(isEven) will return false.
Array.prototype.some is JavaScript’s Existential StatementUniversal Implication
Once you have checked a universal statement against a set, say nums.every(isOdd), it is tempting to think that you can grab an element from the set that satisfies the predicate. However, there is one catch: in Boolean logic, a true universal statement does not imply that the set is non-empty. Universal statements about empty sets are always true, so if you wish to grab an element from a set satisfying some condition, use an existential check instead. To prove this, run [].every(() => false). It will be true.
Universal statements about empty sets are always true.
Negating Universal and Existential Statements
Negating these statements can be surprising. The negation of a universal statement, say nums.every(isOdd), is not nums.every(isEven), but rather nums.some(isEven). This is an existential statement with the predicate negated. Similarly, the negation of an existential statement is a universal statement with the predicate negated.
!arr.every(el => fn(el)) === arr.some(el => !fn(el))!arr.some(el => fn(el)) === arr.every(el => !fn(el))
Set Intersections
Two sets can only be related to each other in a few ways, with regards to their elements. These relationships are easily diagrammed with Venn Diagrams, and can (mostly) be determined in code using combinations of universal and existential statements.
Two sets can each share some but not all of their elements, like a typical conjoined Venn Diagram:

A.some(el => B.includes(el)) && A.some(el => !B.includes(el)) && B.some(el => !A.includes(el)) describes a conjoined pair of setsOne set can contain all of the other set’s elements, but have elements not shared by the second set. This is a subset relationship, denoted as Subset ⊆ Superset.

B.every(el => A.includes(el)) describes the subset relationship B ⊆ AThe two sets can share no elements. These are disjoint sets.

A.every(el => !B.includes(el)) describes a disjoint pair of setsLastly, the two sets can share every element. That is, they are subsets of each other. These sets are equal. In formal logic, we would write A ⊆ B && B ⊆ A ⟷ A === B, but in JavaScript, there are some complications with this. In JavaScript, an Array is an ordered set and may contain duplicate values, so we cannot assume that the bidirectional subset code B.every(el => A.includes(el)) && A.every(el => B.includes(el)) implies the arrays A and B are equal. If A and B are Sets (meaning they were created with new Set()), then their values are unique and we can do the bidirectional subset check to see if A === B.
(A === B) === (Array.from(A).every(el => Array.from(B).includes(el)) && Array.from(B).every(el => Array.from(A).includes(el)), giventhatAand Bare constructedusing newSet()
Translating Logic to English
This section is probably the most useful in the article. Here, now that you know the logical operators, their truth tables, and rules of replacement, you can learn how to translate an English phrase into code and simplify it. In learning this translation skill, you will also be able to read code better, storing complex logic in simple phrases in your mind.
Below is a table of logical code (left) and their English equivalents (right) that was heavily borrowed from the excellent book, Essentials of Logic.

Below, I will go through some real-world examples from my own work where I interpret from English to code, and vice-versa, and simplify code with the rules of replacement.
Example 1
Recently, to satisfy the EU’s GDPR requirements, I had to create a modal that showed my company’s cookie policy and allowed the user to set their preferences. To make this as unobtrusive as possible, we had the following requirements (in order of precedence):
- If the user wasn’t in the EU, never show the GDPR preferences modal.
- 2. If the app programmatically needs to show the modal (if a user action requires more permission than currently allowed), show the modal.
- If the user is allowed to have the less-obtrusive GDPR banner, do not show the modal.
- If the user has not already set their preferences (ironically saved in a cookie), show the modal.
I started off with a series of if statements modeled directly after these requirements:
const isGdprPreferencesModalOpen = ({ shouldModalBeOpen, hasCookie, hasGdprBanner, needsPermissions}) => { if (!needsPermissions) { return false; } if (shouldModalBeOpen) { return true; } if (hasGdprBanner) { return false; } if (!hasCookie) { return true; } return false;}To be clear, the above code works, but returning boolean literals is a code smell. So I went through the following steps:
/* change to a single return, if-else-if structure */let result;if (!needsPermissions) { result = false;} else if (shouldBeOpen) { result = true;} else if (hasBanner) { result = false;} else if (!hasCookie) { result = true} else { result = false;}return result;/* use the definition of ternary to convert to a single return */return !needsPermissions ? false : (shouldBeOpen ? true : (hasBanner ? false : (!hasCookie ? true : false)))/* convert from ternaries to conjunctions of disjunctions */return (!!needsPermissions || false) && (!needsPermissions || ((!shouldBeOpen || true) && (shouldBeOpen || ((!hasBanner || false) && (hasBanner || !hasCookie))))/* simplify double-negations and conjunctions/disjunctions with boolean literals */return needsPermissions && (!needsPermissions || ((!shouldBeOpen || true) && (shouldBeOpen || (!hasBanner && (hasBanner || !hasCookie))))/* DeMorgan's Laws */return needsPermissions && (!needsPermissions || ((!shouldBeOpen || true) && (shouldBeOpen || ((!hasBanner && hasBanner) || (hasBanner && !hasCookie))))/* eliminate tautologies and contradictions, simplify */return needsPermissions && (!needsPermissions || (shouldBeOpen || (hasBanner && !hasCookie)))/* DeMorgan's Laws */return (needsPermissions && !needsPermissions) || (needsPermissions && (shouldBeOpen || (hasBanner && !hasCookie)))/* eliminate contradiction, simplify */return needsPermissions && (shouldBeOpen || (hasBanner && !hasCookie))I ended up with something that I think is more elegant and still readable:
const isGdprPreferencesModalOpen = ({ needsPermissions, shouldBeOpen, hasBanner, hasCookie,}) => ( needsPermissions && (shouldBeOpen || (!hasBanner && !hasCookie)));Example 2
I found the following code (written by a coworker) while updating a component. Again, I felt the urge to eliminate the boolean literal returns, so I refactored it.
const isButtonDisabled = (isRequestInFlight, state) => { if (isRequestInFlight) { return true; } if (enabledStates.includes(state)) { return false; } return true;};Sometimes I do the following steps in my head or on scratch paper, but most often, I write each next step in the code and then delete the previous step.
// convert to if-else-if structurelet result;if (isRequestInFlight) { result = true;} else if (enabledStates.includes(state)) { result = false;} else { result = true;}return result;// convert to ternaryreturn isRequestInFlight ? true : enabledStates.includes(state) ? false : true;/* convert from ternary to conjunction of disjunctions */return (!isRequestInFlight || true) && (isRequestInFlight || ((!enabledStates.includes(state) || false) && (enabledStates.includes(state) || true))/* remove tautologies and contradictions, simplify */return isRequestInFlight || !enabledStates.includes(state)Then I end up with:
const isButtonDisabled = (isRequestInFlight, state) => ( isRequestInFlight || !enabledStates.includes(state));In this example, I didn’t start with English phrases and I never bothered to interpret the code to English while doing the manipulations, but now, at the end, I can easily translate this: “the button is disabled if either the request is in flight or the state is not in the set of enabled states.” That makes sense. If you ever translate your work back to English and it doesn’t make sense, re-check your work. This happens to me often.
Example 3
While writing an A/B testing framework for my company, we had two master lists of Enabled and Disabled experiments and we wanted to check that every experiment (each a separate file in a folder) was recorded in one or the other list but not both. This means the enabled and disabled sets are disjointed and the set of all experiments is a subset of the conjunction of the two sets of experiments. The reason the set of all experiments must be a subset of the combination of the two lists is that there should not be a single experiment that exists outside the two lists.
const isDisjoint = !enabled.some(el => disabled.includes(el)) && !disabled.some(el => enabled.includes(el));const isSubset = allExperiments.every( el => enabled.concat(disabled).includes(el));assert(isDisjoint && isSubset);Conclusion
Hopefully this has all been helpful. Not only are the skills of translating between English and code useful, but having the terminology to discuss different relationships (like conjunctions and implications) and the tools to evaluate them (truth tables) is handy.
