By Michael Olorunnisola
So who wants to work at Google, Facebook, or maybe LinkedIn? Beyond their grueling interview process, one thing all these companies have in common is their heavy reliance on the graph data structure.
After learning a bit about graphs, you’ll understand why. By the end of this post, you’ll feel more comfortable jumping into Cracking the Coding Interview — or a similar interview prep book — and knocking out some network traversal algorithms practice problems.
How Graphs Work
Graphs are a powerful and versatile data structure that easily allow you to represent real life relationships between different types of data (nodes). There are two main parts of a graph:
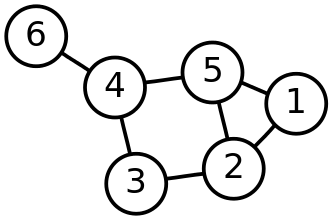
- The vertices (nodes) where the data is stored i.e. the numbers in the image on the left
- The edges (connections) which connect the nodes i.e. the lines between the numbers in the image
Graphs can be undirected or directed. Using the graph above as an example — and treating the edges as every day relationships — here’s the difference:
Undirected graph: If 6 was a friend of 4, 4 would likewise be a friend of 6. The relationship exists in both directions.
Directed graph: if 6 had a crush on 4, that doesn’t necessarily mean 4 has to have a crush on 6. Love’s tough ?. The relationships are based on the direction of the edges. It can _b_e a one way relationship or a two-way relationship, but it must be explicitly stated.
Here are some common operations you can perform on graphs:
Additions
addNode: adds vertices to your graphaddEdge: creates edges between two given vertices in your graph
Removals
removeNode: removes vertices from your graphremoveEdge: removes edges between two given vertices in your graph
Search
contains: checks if your graph contains a given valuehasEdge: checks if a connection exists between two given nodes in your graph
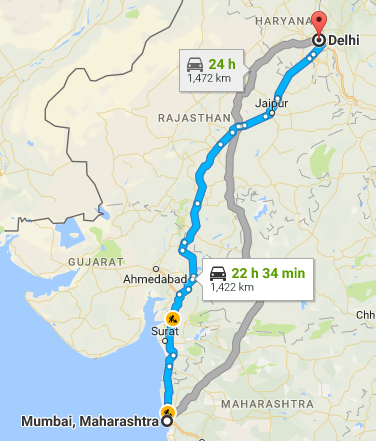
In addition to this, graphs can be weighted or unweighted. All this means is that there is some value or cost associated with the edges between the vertices. The best example of this would be google maps.
As you can see, there are two suggested routes between Mumbai and Delhi. But how would a Google graph algorithm know that one in blue is the best option? Simple. You give the different routes (edges) weights equivalent to their distances. Knowing that, the algorithm can deduce that one path is 50km shorter than the other, and probably faster.
Of course, there are other factors given weight like delays and speed limits. But the concept remains the same. Weighted graphs allow you to choose the quickest path, or the path of least resistance (see Dijkstra’s Algorithm).
As you can see from these examples, graphs can show almost any type of relationship with just data and edges. This is why graphs have become so widely used by companies like LinkedIn, Google, and Facebook. Just read this post by Facebook about why they made the transition back in 2007 from relational databases to graph databases.
Now that you have a basic understanding of what graphs are, let’s explore some examples.
Example Use Cases:
- Representing a social network
- Representing maps
- Killing interview questions
The last one there is up to you. If you’re getting ready for a coding interview, I’ve included some helpful additional resources at the end of this post.
In the mean time, let’s take a stab at social networks.
Building a social network using graphs
Since Facebook kind of has a monopoly on this whole social network thing, how about we create a private social network for developers? DevBook! Of course, we could keep things simple and just create a Facebook group instead… But being grade A developers who love a good challenge, let’s take a prideful moment to throw “KISS” out the window.
First you create the storage for your graph. You realize there are probably multiple ways you can represent a graph data structure, but for now you decide upon a list that will store each unique developer as a key and all their connections as their associated values. Upon running a quick Google search, you realize that you’re making an adjacency list.
You prefer following a functional pattern, so you decide to go the route below:
let MakeGraph = () => { // Function that will create our graphs let graph = {}; return graph;}
let devBook = MakeGraph(); // Our graph representing our site
Now that you have the graph representation, you need to create a way to add developers to the graph when they sign up, and to store any future connections they might have.
You decide to make the users keys on the object, and use an object with an edges property to keep a list of their connections.
let MakeGraph = () => { let graph = {};
graph.addVertex = (node) => { // add members as vertices here // store their connections as properties on an edges object graph[node] = {edges:{}}; }
return graph;}
let devBook = MakeGraph();
devBook.addVertex('James Gosling');devBook.addVertex('Guido Rossum');devBook.addVertex('Linus Torvalds');devBook.addVertex('Michael Olorunnisola');
// Your graph will now look like this:
{ addVertex: [Function], 'James Gosling': { edges: {} }, 'Guido Rossum': { edges: {} }, 'Linus Torvalds': { edges: {} }, 'Michael Olorunnisola': { edges: {} } }
Note that in practice, you would want to store records with unique user id’s instead of names that couldn’t be overwritten by other users with the same name, but I’ve used the names of famous programmers (plus myself) for flavor.
Now you can build a contains method to check whether a user has already been stored on your graph, and prevent the overwriting of any of the relationships that are created as the site grows.
let MakeGraph = () => { let graph = {};
graph.contains = (node)=> { // you can check whether a user exists return !!graph[node]; }
graph.addVertex = (node) => { if(!graph.contains(node)){ // call contains to prevent overwrite graph[node] = {edges:{}}; } }
return graph;}
Great! Now that you have a good set of unique users, you want to let them connect with each other by creating friendships with each other (edges). These edges won’t be directed, as you realize friendships don’t really work that way.
let MakeGraph = () => { let graph = {};
graph.contains = (node)=> { return !!graph[node]; }
graph.addVertex = (node) => { if(!graph.contains(node)){ graph[node] = {edges:{}}; } }
graph.addEdge = (startNode, endNode) => { // Only if both nodes exist // Add each node to the others edge list
if(graph.contains(startNode) && graph.contains(endNode)){ graph[startNode].edges[endNode] = true; graph[endNode].edges[startNode] = true; } }
return graph;}
let devBook = MakeGraph(); // Our graph representing our site
devBook.addVertex('James Gosling');devBook.addVertex('Guido Rossum');devBook.addVertex('Linus Torvalds');devBook.addVertex('Michael Olorunnisola');
// We'll add the edges here!
devBook.addEdge('James Gosling', 'Guido Rossum');devBook.addEdge('Linus Torvalds', 'Michael Olorunnisola');
// Now our devBook will look like this:
{ contains: [Function], addVertex: [Function], addEdge: [Function], 'James Gosling': { edges: { 'Guido Rossum': true } }, 'Guido Rossum': { edges: { 'James Gosling': true } }, 'Linus Torvalds': { edges: { 'Michael Olorunnisola': true } }, 'Michael Olorunnisola': { edges: { 'Linus Torvalds': true } } }
This is absolutely fantastic, but at some point Linus reaches out to you and says, “I have no idea who the Michael guy is. I assumed he was Michael Tiemann, but I finally bothered trying to read his last name.”
Right now you don’t have a way to remove a relationship, so you hop right into the code to whip together a removeEdge method to allow Linus to keep his friends list accurate.
let MakeGraph = () => { let graph = {};
graph.contains = (node)=> { return !!graph[node]; }
graph.addVertex = (node) => { if(!graph.contains(node)){ graph[node] = {edges:{}}; } }
graph.addEdge = (startNode, endNode) => { if(graph.contains(startNode) && graph.contains(endNode)){ graph[startNode].edges[endNode] = true; graph[endNode].edges[startNode] = true; } } graph.removeEdge = (startNode, endNode) => { if(graph.contains(startNode) && graph.contains(endNode)){ delete graph[startNode].edges[endNode] delete graph[endNode].edges[startNode] } }
return graph;}
devBook.removeEdge('Linus Torvalds', 'Michael Olorunnisola');
// Relationship removed!
{ contains: [Function], addVertex: [Function], addEdge: [Function], removeEdge: [Function], 'James Gosling': { edges: { 'Guido Rossum': true } }, 'Guido Rossum': { edges: { 'James Gosling': true } }, 'Linus Torvalds': { edges: {} }, 'Michael Olorunnisola': { edges: {} } }
Great! Unfortunately Linus says that he just wanted to try the site out, but that he’s way to0 hermitic to be on a site like this. He really wants to delete his account, but is currently unable to because you haven’t added a node removal method yet.
let MakeGraph = () => { let graph = {};
graph.contains = (node)=> { return !!graph[node]; }
graph.addVertex = (node) => { if(!graph.contains(node)){ graph[node] = {edges:{}}; } }
graph.removeVertex = (node) => { if(graph.contains(node)) { // We need to remove any existing edges the node has for(let connectedNode in graph[node].edges) { graph.removeEdge(node, connectedNode); } delete graph[node]; }
}
graph.addEdge = (startNode, endNode) => { if(graph.contains(startNode) && graph.contains(endNode)){ graph[startNode].edges[endNode] = true; graph[endNode].edges[startNode] = true; } } graph.removeEdge = (startNode, endNode) => { if(graph.contains(startNode) && graph.contains(endNode)){ delete graph[startNode].edges[endNode] delete graph[endNode].edges[startNode] } }
return graph;}
// Now we can remove users!
devBook.removeVertex('Linus Torvalds');
Great job! Although you lost a potentially valuable user, you’ve been able to implement a basic graph system to keep track of all of your users and their friendships.
If you notice, we didn’t implement the hasEdge method, but I think you have enough information to give it a shot! Feel free to include your implementation in the comments below ?.
A time complexity analysis on the graph methods as an adjacency list
Here’s our code again:
let MakeGraph = () => { let graph = {};
graph.contains = (node)=> { return !!graph[node]; }
graph.addVertex = (node) => { if(!graph.contains(node)){ graph[node] = {edges:{}}; } }
graph.removeVertex = (node) => { if(graph.contains(node)) { for(let connectedNode in graph[node].edges) { graph.removeEdge(node, connectedNode); } delete graph[node]; } }
graph.addEdge = (startNode, endNode) => { if(graph.contains(startNode) && graph.contains(endNode)){ graph[startNode].edges[endNode] = true; graph[endNode].edges[startNode] = true; } } graph.removeEdge = (startNode, endNode) => { if(graph.contains(startNode) && graph.contains(endNode)){ delete graph[startNode].edges[endNode] delete graph[endNode].edges[startNode] } }
return graph;}
addNode is O(1): You’re just creating a property on an object so it’s constant time
addEdge is O(1): Since you’re using an object to represent your graph, it’s a constant time operation since your nodes and edges are represented as properties.
removeNode is O(n): If a node has edges, you’re going to have to iterate over all it’s existing edges to remove it’s existence as an edge on it’s connected nodes.
removeEdge is O(1): Since your nodes are properties on your graph, you can access them in constant time and just delete the edges which are also accessible in constant time.
contains is O(1): As a property on your graph, it’s a constant time lookup for a node.
hasEdge is O(1): Both nodes would be properties on your graph, so it would be a constant time lookup.
Time for a quick recap
Graphs:
- are just a combination of vertices and edges representing data and relationships
- have
addNode,addEdge,removeNode, andremoveEdgemethods to manage their contents - have a
containsand ahasEdgemethod to help you track the state of their state
Further Reading
To say that there is a lot more to the graph data structure would be a huge understatement.
You could have represented the edges as an array instead of objects, or the entire graph as a 2-d array (adjacency matrix). You could have even represented the graph solely by their edges in an array (edge list).
As with anything in programming, there are trade-offs associated with each representation and it’s definitely worthwhile learning what they are.
Graphs are by far my favorite data structure and also one of the most versatile, but that’s just my humble opinion. (Those of you who love trees really are just graph lovers in disguise ?).
Maybe I can sway you to love them as much as I do, so here are a few additional resources for you to read up on them:
- This Wikipedia Article does a great job not only covering the different representation of a graph, but also introducing you to some of the algorithms often associated with graphs.
- For those of you who are using Python here’s a graph implementation from the Python team!
- TutorialsPoint does a really good job of diving into how to implement two of the algorithms: Depth First Search and Breadth First Search. You might be confronted with these graph algorithms in interviews.
- Keith Woods does a great job of walking through how to implement a recommendation engine with a graph data structure here. Definitely worth a read, as it implements a lot of the concepts we didn’t get to here.
- For those of you who are familiar with relational databases like MySQL — there’s a Graph database Neo4j, which I absolutely love, that not only uses SQL-like syntax, but has an awesome graphical user interface.