By Ben Weber
The recent tax reform bill passed in the US has raised a lot of questions about wealth distribution in the country. While there’s been a lot of focus on how the tax plan will impact income, there’s been less attention focused on how this plan impacts the assets of wealthy households.
The goal of this post is to show how the R programming language can be used to data mine publicly available sources to better understand the net worth of affluent households in the US. Using data from the 2016 Federal Reserve Survey of Consumer Finances, we investigate the following questions:
- How rich are the top 1% and top 0.1% of households?
- Are there different types of millionaires in the US?
- How do asset allocations differ across different net worth segments?
To answer these questions, we present descriptive statistics of this survey data and perform cluster analysis on affluent households, which we identify as households with a net worth of more than $1,000,000 USD.
Based on the survey data, our analysis shows that the net worth of the top 1% of households in the US is $10.4M and the net worth of the top 0.1% of households is $43.2M. This post presents an analysis of the different asset compositions of millionaires, and shows how asset allocations differ between the top 10%, 1%, and 0.1% of households in the US. The R source code used to produce all results and figures presented in this post is available as a Jupyter Notebook.
Setting Up the Environment
To perform cluster analysis on the affluent households in the US, we use several packages available from the CRAN library for R. For exploratory data analysis, we like to use the R kernel for the Jupyter notebook, since it enables data scientists to easily store notebooks on GitHub and share findings with other teams.
Setting up this environment is outside the scope of this post, but I’ve previously detailed our motivation for this setup in this post, and additional details for setting up Jupyter with R support are available here.
We’re now ready to start digging into the survey data to better understand the assets of affluent households in the US. To begin, we’ll load several libraries that will help us analyze the survey data and perform clustering.
The code block below shows the libraries that need to be loaded for executing this notebook. The readxl library is needed to read the source data and convert it into a data frame, the reldist and ENmisc libraries are used for computing distributions with weighted data sets, and the remaining libraries are used for cluster analysis.
library(readxl) # for reading xlsx files library(reldist) # for computing weighted statisticslibrary(ENmisc) # for weighted box plotslibrary(plotly) # for interactive plotslibrary(factoextra) # for factor mapslibrary(FactoMineR) # Principal Component Analysis (PCA)library(cluster) # Clustering algorithms (CLARA)library(class) # for KNN
Getting the Data
The next step is to download the data from the Federal Reserve website. The survey data is available as a zipped xlsx file. To download the data and load it into R as a data frame for analysis, we use the code block below. Since this is a large file, we make sure that we do not download it multiple times. The resulting file that we unzip is about 40MB and takes some time to load into a data frame.
if (!file.exists("SCFP2016.xlsx")) { download.file( "https://www.federalreserve.gov/econres/files/scfp2016excel.zip", "SCFP2016.zip") unzip("scfp2016.zip")}
df <- read_excel("SCFP2016.xlsx")
Summary Statistics
Now that we have the survey data loaded into R, we can start to analyze the asset allocation of the richest households in the US. We’ll start with some summary stats: how many survey participants and how many households are represented by this survey? Counting the number of rows in the data frame answers the first questions (31.2k), and adding up the weights of all of the survey respondents answers the second question (126M).
# How many survey participants?nrow(df)
# How many households does the survey represent?floor(sum(df$WGT)))
# What is the weighted mean of household net worth?floor(sum(df$NETWORTH*df$WGT)/sum(df$WGT)))
# what is the median NW in US? reldist::wtd.quantile(df$NETWORTH, q=0.5, weight = df$WGT)
# who is the 1%? reldist::wtd.quantile(df$NETWORTH, q=0.99, weight = df$WGT)
# top 0.1% Ultra-high net worth households reldist::wtd.quantile(df$NETWORTH, q=0.999, weight = df$WGT)
To answer questions about averages, such as what is the mean household net worth, we need to use weighted statistics (since the weight of one survey respondent can be much larger than others). To compute the mean net worth, we can use built-in R functions, which returns a value of $690k. However, since net worth is much closer to a log normal than normal distribution, we should use other approaches.
To compute the median value with weighted responses, we use the reldist library, which assigns more support to respondents with larger weights and less support to respondents with lower weights. When using this approach to compute the weighted median, we find that the 50th percentile for household net worth in the US is $97k.
The net worth of the top 1% is $10.4M and the net worth of the top 0.1% is $43.2M. We use the wtd.quantile function to compute these descriptive statistics, and the code sample above uses the fully quantified function names, due to collisions with the ENmisc package.
Demographic Data
The survey data provides a number of different demographic variables that can be used to analyze net worth by different factors. These variables include race, marital status, education level, employment status, and others. The goal of this post is to show how asset allocation varies by net worth segment, and analysis of how these demographic factors impact net worth is left as an exercise for the reader.
# filter on ages 30 - 84, and group into 5-year bucketsdata <- df[df$AGE >= 30 & df$AGE < 85, ]ages <- floor(data$AGE/5.0)*5
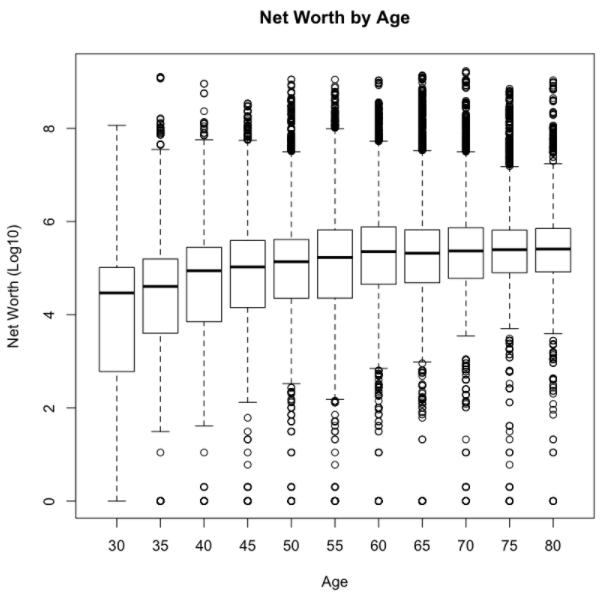
# plot the weighted box plotwtd.boxplot(log10(1 + data$NETWORTH) ~ ages, data = data, weights = data$WGT, main = 'Net Worth by Age', xlab="Age", ylab="Net Worth (Log10)")
One demographic variable that we did explore is the impact of age on household net worth. As expected, the median net worth does increase as the head of household becomes older, with net worth plateauing around 60 years old.
The code above shows how to display a box plot of the survey data by age, using the ENmisc package to compute weighted distributions. The results of this plot show that the median net worth of households in the US are $114k at 40, $163k at 50, and $243k at 60.
Asset Allocation
The next step in the notebook is to evaluate the asset allocation of different net worth segments. For this analysis, we define a segment based on the log10 value of the household net worth. That means all 5-figure households get grouped together, all 6-figure households get grouped together, as so on.
# normalize assets by total financial and non-financial amountshouseholds <- data.frame( LIQ = df$LIQ/assets, ... BUS = df$BUS/assets, OTHNFIN = df$OTHNFIN/assets
# split into net worth segments, and compute mean distributions nw <- floor(log10(households$netWorth))segment <- ifelse(nw == 4, " $10k", ifelse(nw == 5, " $100K", ifelse(nw == 6, " $1M", ifelse(nw == 7, " $10M", ifelse(nw == 8, " $100M", "$1B+")))))
results <- as.data.frame((aggregate(households,list(segment),mean)))
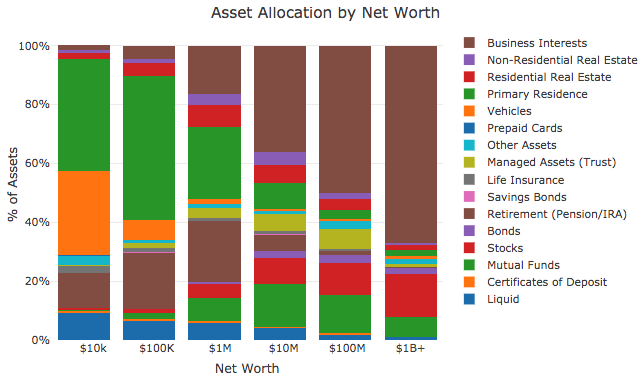
# plot the resultsplot <- plot_ly(results, x = ~Group.1, y = ~100*LIQ, type = 'bar', name = 'Liquid') %>% add_trace(y = ~100*CDS, name = 'Certificates of Deposit') %>% add_trace(y = ~100*NMMF, name = 'Mutual Funds') %>% ... add_trace(y = ~100*BUS, name = 'Business Interests') %>% layout(yaxis = list(title = '% of Assets', ticksuffix = "%"), xaxis = list(title = "Net Worth"), title = "Asset Allocation by Net Worth", barmode = 'stack')
The code above computes the asset allocation by household, by dividing the amount of assets for a household, such as business equity (BUS) over the total number of financial and non-financial assets, excluding debt. The “…” pattern is used to indicate that multiple rows have been excluded from the code snippet that are listed in the full notebook. The second code block groups the households into different net worth segments, and the third block plots the results as shown below.
The results show that the wealthy, ultra wealthy, and billionaires have large amounts of assets in business equity (stock and options). The wealthy have only a small percentage of assets in retirement funds, and instead have assets in stock, mutual funds, and residential and commercial real estate.
Clustering Millionaires
So far, we’ve looked at aggregate statistics of wealthy households, but that doesn’t tell us about the different types of affluent households. To understand how assets vary across affluent homes, we can use cluster analysis. One of the most useful ways to visualize the difference between instances in a sample population is to use factor maps to visualize the variance in the population.
# filter on affluent households, and print the total numberaffluent <- households[households$netWorth >= 1000000, ]cat(paste("Affluent Households: ", floor(sum(affluent$weight))))
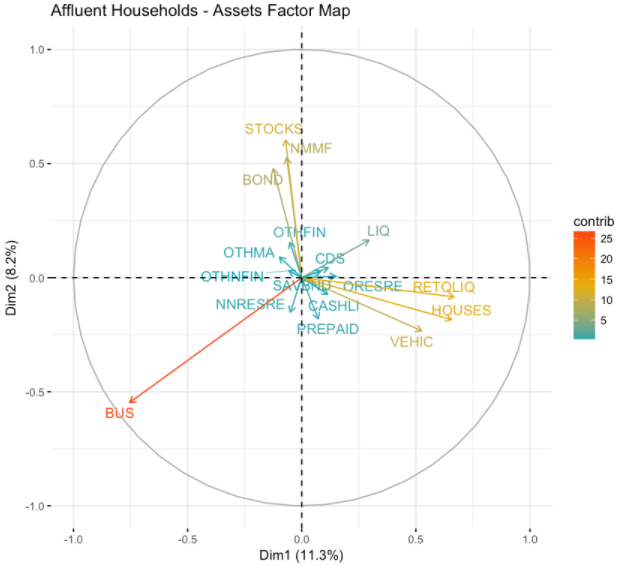
# plot a Factor Map of assets fviz_pca_var(PCA(affluent, graph = FALSE), col.var="contrib", gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), repel = TRUE)+ labs(title ="Affluent Households - Assets Factor Map")
The code above first filters survey respondents to affluent households, with a net worth of more than $1M USD, and then plots a factor map using principal component analysis (PCA). The figure below shows how the different assets impact the trajectory of plotting a household across the two principal components discovered via PCA.
The results plotted below show that there are a few different assets groups that vary across affluent net worth. The most significant factor is business equity. Some other groupings of factors include investment assets (STOCKS, BONDS) and real estate assets/retirement funds.
How many clusters to use?
We’ve now shown signs that there are different types of millionaires, and that assets vary based on net worth segments. To understand how asset allocation differs by net worth segment, we can use cluster analysis. We first identify clusters in the affluent survey respondents, and then apply these labels to the overall population of survey respondents.
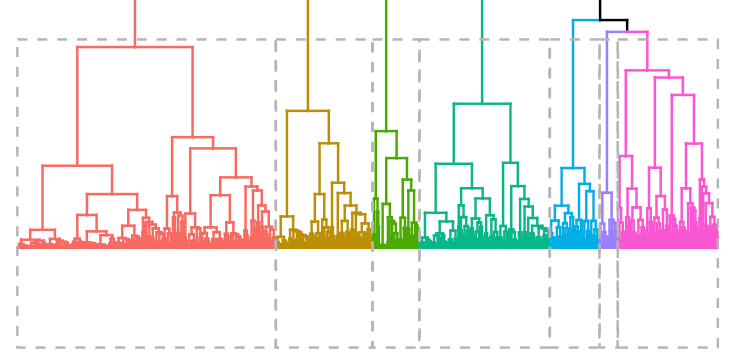
k <- 7res.hc <- eclust(households[sample(nrow(households), 1000), ], "hclust", k = k, graph = FALSE) fviz_dend(res.hc, rect = TRUE, show_labels = FALSE)
To determine how many clusters to use, we created a cluster dendrogram using the code snippet above, shown as the header image of this post. We also varied the number of clusters, k, until we had the largest number of distinctly identifiable clusters.
If you’d prefer to take a quantitative approach, you can use the _fviznbclust function, which computes the optimal number of clusters using a silhouette metric. For our analysis, we decided to use 7 clusters.
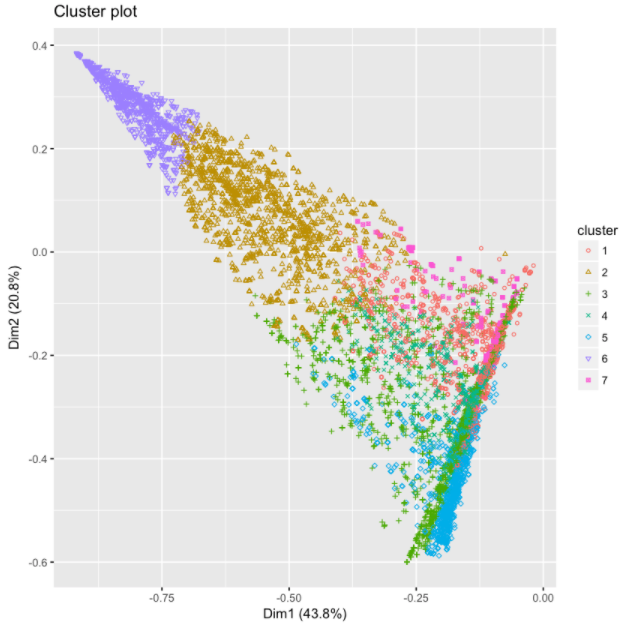
clarax <- clara(affluent, k)fviz_cluster(clarax, stand = FALSE, geom = "point", ellipse = F)
To cluster the affluent households into unique groupings, we used the CLARA algorithm. A visualization of the different clusters is shown below. The results are similar to PCA and the factor map approach discussed above.
Cluster Descriptions
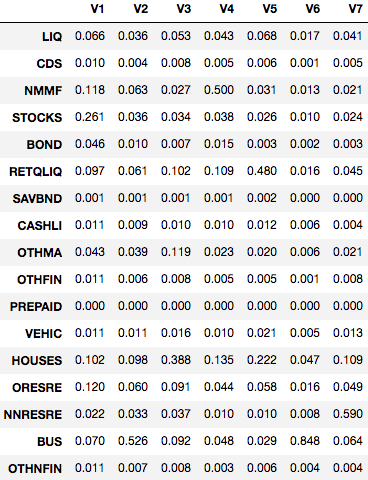
Now that we’ve determined how many clusters to use, it’s useful to inspect the clusters and assign qualitative labels based on the feature sets. The code snippet below shows how to compute the average feature values for the 7 different clusters.
groups <- clarax$clusteringresults <- as.data.frame(t(aggregate(affluent,list(groups),mean))) results[2:18,]
The results of this code block are shown below. Based on these results, we came up with the following cluster descriptions:
- V1: Stocks/Bonds — 31% of assets, followed by home and mutual funds
- V2: Diversified — 53% busequity, 10% home and 9% in other real estate
- V3: Residential Real Estate — 48% of assets
- V4: Mutual Funds — 50% of assets
- V5: Retirement — 48% of assets
- V6: Business Equity — 85% of assets
- V7: Commercial Real Estate — 59% of assets
With the exception of cluster V7, containing only 3% of the population, most of the clusters are relatively even in size. The second smallest cluster represents 12% of the population while the largest cluster represents 20%. You can use table(groups) to show the unweighted cluster population sizes.
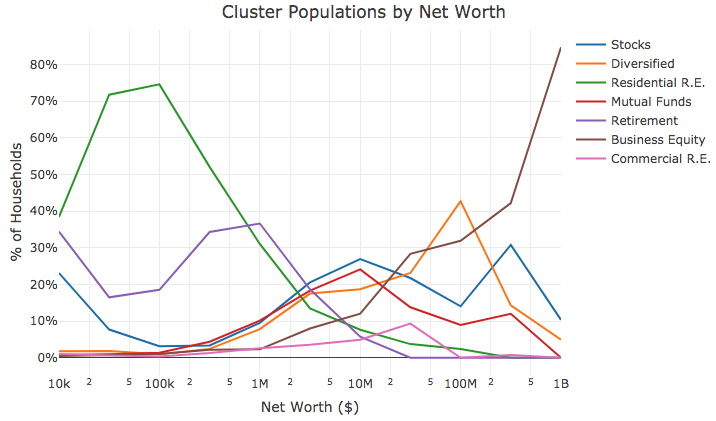
Cluster Populations by Net Worth Segments
The last step in this analysis is to apply the different cluster assignments to the overall population, and to group the populations by net worth segments. Since we trained the clusters on only affluent households, we need to use a classification algorithm to label the non-affluent households in the population. The code snippet below uses knn to accomplish this task.
The remaining code blocks compute the number of households that are classified as each cluster, for each of the net worth segments.
# assign all of the households to a cluster groups <- knn(train = affluent, test = households, cl = clarax$clustering, k = k, prob = T, use.all = T)
# figure out how many households are in each cluster clusters <- data.frame( c1 = ifelse(groups == 1, weights, 0), ... c7 = ifelse(groups == 7, weights, 0) )
# assign each household to a net worth cluster nw <- floor(2*log10(nwHouseholds))/2results <- as.data.frame(t(aggregate(clusters,list(nw),sum)))
# compute the number of households that belong to each segmentresults$V1 <- results$V1/sum(ifelse(nw == 4, weights, 0))...results$V11 <- results$V11/sum(ifelse(nw == 9, weights, 0))
# plot the results plot <- plot_ly(results, x = ~10^Group.1, y = ~100*c1, type = 'scatter', mode = 'lines', name = "Stocks") %>% add_trace(y = ~100*c2, name = "Diversified") %>% ... add_trace(y = ~100*c7, name = "Commercial R.E.") %>% layout(yaxis = list(title = '% of Households', ticksuffix = "%"), xaxis = list(title = "Net Worth ($)", type = "log"), title = "Cluster Populations by Net Worth")
The results of this process are shown in the figure below. The chart shows some obvious and some novel results: home ownership and retirement funds make up the majority of assets for non-affluent households, there is a relatively even mix of clusters around $2M (excluding commercial real estate and business equity), and business equity dominates net worth for the ultra-wealthy households, followed by other investment assets.
Summary
In this post we used R to download and analyze data from the 2016 Federal Reserve survey of consumer finances to understand how wealthy the top households are in the US, and to cluster affluent households by asset allocation. We identified 7 distinct groups of millionaires, and showed how the distribution of clusters varies based on net worth segment. Please keep in mind that the results presented are from weighted survey data, and may not be representative of the overall US population.
Ben Weber is a principal data scientist at Zynga. We are hiring!