Hi everyone! In this article we're going to take a look at a key topic when it comes to computer science and software development: data structures.
It's definitely a must know topic for anyone working in the software development world, but it can be hard to understand and even a bit intimidating when you're starting out.
In this article I'll try to give a simple explanation of data structures, what they are, when are they useful, and how we can implement them using JavaScript.
Let's go!
Table of contents
What is a data structure?
In computer science, a data structure is a format to organize, manage and store data in a way that allows efficient access and modification.
More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to that data.
These definitions might sound a bit abstract at first, but think about it. If you've been coding for a little while, you must have used data structures before.
Have you used arrays and objects? Those are all data structures. All of them are a collection of values that relate to each other, and can be operated on by you.😉
// A collection of the values 1, 2 and 3
const arr = [1, 2, 3]
// Each value is related to one another, in the sense that each is indexed in a position of the array
const indexOfTwo = arr.indexOf(2)
console.log(arr[indexOfTwo-1]) // 1
console.log(arr[indexOfTwo+1]) // 3
// We can perform many operations on the array, like pushing new values into it
arr.push(4)
console.log(arr) // [1,2,3,4]
JavaScript has primitive (built in) and non-primitive (not built in) data structures.
Primitive data structures come by default with the programming language and you can implement them out of the box (like arrays and objects). Non-primitive data structures don't come by default and you have to code them up if you want to use them.
Different data structures exist because some of them are better suited for certain kind of operations. You will probably be able to tackle most programming tasks with built-in data structures, but for some very specific tasks a non-primitive data structure may come in handy.
Now let's go through the most popular data structures out there, and see how each of them works, in what occasions they're useful, and how we can code them up in JavaScript.
Arrays
An array is a collection of items stored at contiguous memory locations.
Each item can be accessed through its index (position) number. Arrays always start at index 0, so in an array of 4 elements we could access the 3rd element using the index number 2.
const arr = ['a', 'b', 'c', 'd']
console.log(arr[2]) // c
The length property of an array is defined as the number of elements it contains. If the array contains 4 elements, we can say the array has a length of 4.
const arr = ['a', 'b', 'c', 'd']
console.log(arr.length) // 4
In some programming languages, the user can only store values of the same type in one array and the length of the array has to be defined at the moment of its creation and can't be modified afterwards.
In JavaScript that's not the case, as we can store values of any type in the same array and the length of it can be dynamic (it can grow or shrink as much as necessary).
const arr = ['store', 1, 'whatever', 2, 'you want', 3]
Any data type can be stored in an array, and that includes arrays too. An array that has other arrays within itself is called a multidimensional array.
const arr = [
[1,2,3],
[4,5,6],
[7,8,9],
]
In JavaScript, arrays come with many built-in properties and methods we can use with different purposes, such as adding or deleting items from the array, sorting it, filtering its values, know its, length and so on. You can find a full list of array methods here. 😉
As I mentioned, in arrays, each element has an index defined by its position in the array. When we add a new item at the end of the array, it just takes the index number that follows the previous last item in the array.
But when we add/delete a new item at the beginning or the middle of the array, the indexes of all the elements that come after the element added/deleted have to be changed. This of course has a computational cost, and is one of the weaknesses of this data structure.
Arrays are useful when we have to store individual values and add/delete values from the end of the data structure. But when we need to add/delete from any part of it, there are other data structures that perform more efficiently (we'll talk about them later on).
Objects (hash tables)
In JavaScript, an object is a collection of key-value pairs. This data structure is also called map, dictionary or hash-table in other programming languages.
A typical JS object looks like this:
const obj = {
prop1: "I'm",
prop2: "an",
prop3: "object"
}
We use curly braces to declare the object. Then declare each key followed by a colon, and the corresponding value.
An important thing to mention is that each key has to be unique within the object. You can't have two keys with the same name.
Objects can store both values and functions. When talking about objects, values are called properties, and functions are called methods.
const obj = {
prop1: "Hello!",
prop3: function() {console.log("I'm a property dude!")
}}
To access properties you can use two different syntaxes, either object.property or object["property"]. To access methods we call object.method().
console.log(obj.prop1) // "Hello!"
console.log(obj["prop1"]) // "Hello!"
obj.prop3() // "I'm a property dude!"
The syntax to assign new values is quite similar:
obj.prop4 = 125
obj["prop5"] = "The new prop on the block"
obj.prop6 = () => console.log("yet another example")
console.log(obj.prop4) // 125
console.log(obj["prop5"]) // "The new prop on the block"
obj.prop6() // "yet another example"
Like arrays, in JavaScript objects come with many built-in methods that allow us to perform different operations and get information from a given object. A full list can be found here.
Objects are a good way to group together data that have something in common or are somehow related. Also, thanks to the fact that property names are unique, objects come in handy when we have to separate data based on a unique condition.
An example could be counting how many people like different foods:
const obj = {
pizzaLovers: 1000,
pastaLovers: 750,
argentinianAsadoLovers: 12312312312313123
}
Stacks
Stacks are a data structure that store information in the form of a list. They allow only adding and removing elements under a LIFO pattern (last in, first out). In stacks, elements can't be added or removed out of order, they always have to follow the LIFO pattern.
To understand how this works, imagine a stack of papers on top of your desk. You can only add more papers to the stack by placing them on top of all the others. And you can remove a paper from the stack only by taking the one that is on top of all the others. Last in, first out. LIFO. 😉

A stack of papers
Stacks are useful when we need to make sure elements follow the LIFO pattern. Some examples of stack usage are:
JavaScript's call stack.
Managing function invocations in various programming languages.
The undo/redo functionality many programs offer.
There's more than one way to implement a stack, but probably the simplest is using an array with its push and pop methods. If we only use pop and push for adding and deleting elements, we'll always follow the LIFO pattern and so operate over it like a stack.
Another way is to implement it like a list, which may look like this:
// We create a class for each node within the stack
class Node {
// Each node has two properties, its value and a pointer that indicates the node that follows
constructor(value){
this.value = value
this.next = null
}
}
// We create a class for the stack
class Stack {
// The stack has three properties, the first node, the last node and the stack size
constructor(){
this.first = null
this.last = null
this.size = 0
}
// The push method receives a value and adds it to the "top" of the stack
push(val){
var newNode = new Node(val)
if(!this.first){
this.first = newNode
this.last = newNode
} else {
var temp = this.first
this.first = newNode
this.first.next = temp
}
return ++this.size
}
// The pop method eliminates the element at the "top" of the stack and returns its value
pop(){
if(!this.first) return null
var temp = this.first
if(this.first === this.last){
this.last = null
}
this.first = this.first.next
this.size--
return temp.value
}
}
const stck = new Stack
stck.push("value1")
stck.push("value2")
stck.push("value3")
console.log(stck.first) /*
Node {
value: 'value3',
next: Node { value: 'value2', next: Node { value: 'value1', next: null } }
}
*/
console.log(stck.last) // Node { value: 'value1', next: null }
console.log(stck.size) // 3
stck.push("value4")
console.log(stck.pop()) // value4
The big O of stack methods is the following:
Insertion - O(1)
Removal - O(1)
Searching - O(n)
Access - O(n)
Queues
Queues work in a very similar way to stacks, but elements follow a different pattern for add and removal. Queues allow only a FIFO pattern (first in, first out). In queues, elements can't be added or removed out of order, they always have to follow the FIFO pattern.
To understand this, picture people making a queue to buy food. The logic here is that if you get the the queue first, you'll be the first to be served. If you get there first, you'll be the first out. FIFO.😉

A queue of clients
Some examples of queue usage are:
Background tasks.
Printing/task processing.
Same as with stacks, there's more than one way to implement a queue. But probably the simplest is using an array with its push and shift methods.
If we only use push and shift for adding and deleting elements, we'll always follow the FIFO pattern and so operate over it like a queue.
Another way is to implement it like a list, which may look like this:
// We create a class for each node within the queue
class Node {
// Each node has two properties, its value and a pointer that indicates the node that follows
constructor(value){
this.value = value
this.next = null
}
}
// We create a class for the queue
class Queue {
// The queue has three properties, the first node, the last node and the queue size
constructor(){
this.first = null
this.last = null
this.size = 0
}
// The enqueue method receives a value and adds it to the "end" of the queue
enqueue(val){
var newNode = new Node(val)
if(!this.first){
this.first = newNode
this.last = newNode
} else {
this.last.next = newNode
this.last = newNode
}
return ++this.size
}
// The dequeue method eliminates the element at the "beginning" of the queue and returns its value
dequeue(){
if(!this.first) return null
var temp = this.first
if(this.first === this.last) {
this.last = null
}
this.first = this.first.next
this.size--
return temp.value
}
}
const quickQueue = new Queue
quickQueue.enqueue("value1")
quickQueue.enqueue("value2")
quickQueue.enqueue("value3")
console.log(quickQueue.first) /*
Node {
value: 'value1',
next: Node { value: 'value2', next: Node { value: 'value3', next: null } }
}
*/
console.log(quickQueue.last) // Node { value: 'value3, next: null }
console.log(quickQueue.size) // 3
quickQueue.enqueue("value4")
console.log(quickQueue.dequeue()) // value1
The big O of queue methods is the following:
Insertion - O(1)
Removal - O(1)
Searching - O(n)
Access - O(n)
Linked lists
Linked lists are a type of data structure that store values in the form of a list. Within the list, each value is considered a node, and each node is connected with the following value in the list (or null in case the element is the last in the list) through a pointer.
There are two kinds of linked lists, singly linked lists and doubly linked lists. Both work very similarly, but the difference is in singly linked lists each node has a single pointer that indicates the next node on the list. While in doubly linked lists, each node has two pointers, one pointing to the next node and another pointing to the previous node.
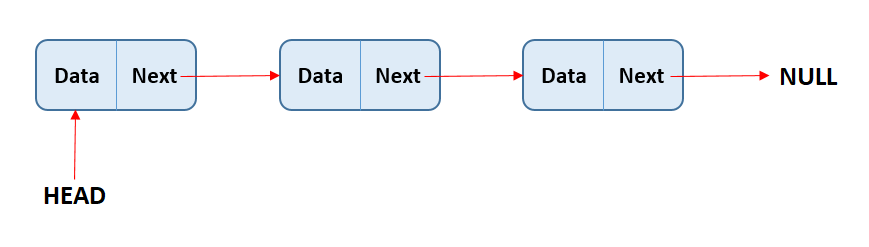
In singly linked list each node has a single pointer
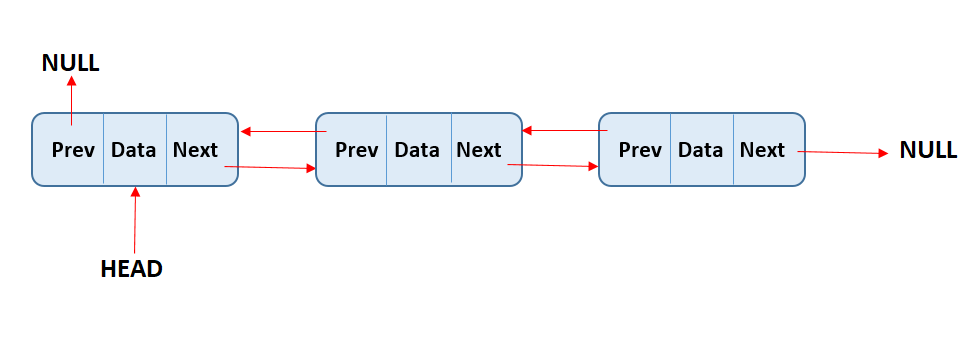
In doubly linked list each node has a two pointers
The first element of the list is considered the head, and the last element is considered the tail. Like with arrays, the length property is defined as the number of elements the list contains.
The main differences compared with arrays are the following:
Lists don't have indexes. Each value only "knows" the values to which it's connected through pointers.
Since lists don't have indexes, we can't access values randomly. When we want to access a value, we always have to look for it by iterating through the list starting from its head or tail.
The good thing of not having indexes, is that insertion/deletion in any part of the list is more efficient than with arrays. We just have to redirect the pointers of the "neighbor" values, while in arrays, values need to be re-indexed.
Like any data structure, different methods are implemented in order to operate over the data. The most common ones include: push, pop, unshift, shift, get, set, insert, remove, and reverse.
First let's see how to implement a singly linked list and then a doubly linked list.
Singly linked list
A full implementation of a singly linked list could look like this:
// We create a class for each node within the list
class Node{
// Each node has two properties, its value and a pointer that indicates the node that follows
constructor(val){
this.val = val
this.next = null
}
}
// We create a class for the list
class SinglyLinkedList{
// The list has three properties, the head, the tail and the list size
constructor(){
this.head = null
this.tail = null
this.length = 0
}
// The push method takes a value as parameter and assigns it as the tail of the list
push(val) {
const newNode = new Node(val)
if (!this.head){
this.head = newNode
this.tail = this.head
} else {
this.tail.next = newNode
this.tail = newNode
}
this.length++
return this
}
// The pop method removes the tail of the list
pop() {
if (!this.head) return undefined
const current = this.head
const newTail = current
while (current.next) {
newTail = current
current = current.next
}
this.tail = newTail
this.tail.next = null
this.length--
if (this.length === 0) {
this.head = null
this.tail = null
}
return current
}
// The shift method removes the head of the list
shift() {
if (!this.head) return undefined
var currentHead = this.head
this.head = currentHead.next
this.length--
if (this.length === 0) {
this.tail = null
}
return currentHead
}
// The unshift method takes a value as parameter and assigns it as the head of the list
unshift(val) {
const newNode = new Node(val)
if (!this.head) {
this.head = newNode
this.tail = this.head
}
newNode.next = this.head
this.head = newNode
this.length++
return this
}
// The get method takes an index number as parameter and returns the value of the node at that index
get(index) {
if(index < 0 || index >= this.length) return null
const counter = 0
const current = this.head
while(counter !== index) {
current = current.next
counter++
}
return current
}
// The set method takes an index number and a value as parameters, and modifies the node value at the given index in the list
set(index, val) {
const foundNode = this.get(index)
if (foundNode) {
foundNode.val = val
return true
}
return false
}
// The insert method takes an index number and a value as parameters, and inserts the value at the given index in the list
insert(index, val) {
if (index < 0 || index > this.length) return false
if (index === this.length) return !!this.push(val)
if (index === 0) return !!this.unshift(val)
const newNode = new Node(val)
const prev = this.get(index - 1)
const temp = prev.next
prev.next = newNode
newNode.next = temp
this.length++
return true
}
// The remove method takes an index number as parameter and removes the node at the given index in the list
remove(index) {
if(index < 0 || index >= this.length) return undefined
if(index === 0) return this.shift()
if(index === this.length - 1) return this.pop()
const previousNode = this.get(index - 1)
const removed = previousNode.next
previousNode.next = removed.next
this.length--
return removed
}
// The reverse method reverses the list and all pointers so that the head becomes the tail and the tail becomes the head
reverse(){
const node = this.head
this.head = this.tail
this.tail = node
let next
const prev = null
for(let i = 0; i < this.length; i++) {
next = node.next
node.next = prev
prev = node
node = next
}
return this
}
}
Singly linked lists methods have the following complexities:
Insertion - O(1)
Removal - O(n)
Search - O(n)
Access - O(n)
Doubly linked lists
As mentioned, the difference between doubly and singly linked lists is that doubly linked lists have their nodes connected through pointers with both the previous and the next value. On the other hand, singly linked lists only connect their nodes with the next value.
This double pointer approach allows doubly linked lists to perform better with certain methods compared to singly linked lists, but at a cost of consuming more memory (with doubly linked lists we need to store two pointers instead of one).
A full implementation of a doubly linked list might look a bit like this:
// We create a class for each node within the list
class Node{
// Each node has three properties, its value, a pointer that indicates the node that follows and a pointer that indicates the previous node
constructor(val){
this.val = val;
this.next = null;
this.prev = null;
}
}
// We create a class for the list
class DoublyLinkedList {
// The list has three properties, the head, the tail and the list size
constructor(){
this.head = null
this.tail = null
this.length = 0
}
// The push method takes a value as parameter and assigns it as the tail of the list
push(val){
const newNode = new Node(val)
if(this.length === 0){
this.head = newNode
this.tail = newNode
} else {
this.tail.next = newNode
newNode.prev = this.tail
this.tail = newNode
}
this.length++
return this
}
// The pop method removes the tail of the list
pop(){
if(!this.head) return undefined
const poppedNode = this.tail
if(this.length === 1){
this.head = null
this.tail = null
} else {
this.tail = poppedNode.prev
this.tail.next = null
poppedNode.prev = null
}
this.length--
return poppedNode
}
// The shift method removes the head of the list
shift(){
if(this.length === 0) return undefined
const oldHead = this.head
if(this.length === 1){
this.head = null
this.tail = null
} else{
this.head = oldHead.next
this.head.prev = null
oldHead.next = null
}
this.length--
return oldHead
}
// The unshift method takes a value as parameter and assigns it as the head of the list
unshift(val){
const newNode = new Node(val)
if(this.length === 0) {
this.head = newNode
this.tail = newNode
} else {
this.head.prev = newNode
newNode.next = this.head
this.head = newNode
}
this.length++
return this
}
// The get method takes an index number as parameter and returns the value of the node at that index
get(index){
if(index < 0 || index >= this.length) return null
let count, current
if(index <= this.length/2){
count = 0
current = this.head
while(count !== index){
current = current.next
count++
}
} else {
count = this.length - 1
current = this.tail
while(count !== index){
current = current.prev
count--
}
}
return current
}
// The set method takes an index number and a value as parameters, and modifies the node value at the given index in the list
set(index, val){
var foundNode = this.get(index)
if(foundNode != null){
foundNode.val = val
return true
}
return false
}
// The insert method takes an index number and a value as parameters, and inserts the value at the given index in the list
insert(index, val){
if(index < 0 || index > this.length) return false
if(index === 0) return !!this.unshift(val)
if(index === this.length) return !!this.push(val)
var newNode = new Node(val)
var beforeNode = this.get(index-1)
var afterNode = beforeNode.next
beforeNode.next = newNode, newNode.prev = beforeNode
newNode.next = afterNode, afterNode.prev = newNode
this.length++
return true
}
}
The big O of doubly linked lists methods is the following:
Insertion - O(1)
Removal - O(1)
Search - O(n)
Access - O(n)
Trees
Trees are a data structures that link nodes in a parent/child relationship, in the sense that there're nodes that depend on or come off other nodes.

A tree
Trees are formed by a root node (the first node on the tree), and all the nodes that come off that root are called children. The nodes at the bottom of the tree, which have no "descendants", are called leaf nodes. And the height of the tree is determined by the number of parent/child connections it has.
Unlike linked lists or arrays, trees are non linear, in the sense that when iterating the tree, the program flow can follow different directions within the data structure and hence arrive at different values.
While on linked lists or arrays, the program can only iterate the data structure from one extreme of it to the other, always following the same path.
An important requirement for tree formation is that the only valid connection between nodes is from parent to child . Connection between siblings or from child to parent are not allowed in trees (these types of connections form graphs, a different type of data structure). Another important requirement is that trees must have only one root.
Some examples of tree usage in programming are:
The DOM model.
Situation analysis in artificial intelligence.
File folders in operating systems.
There're many different types of trees. In each type of tree, values may be organized following different patterns that make this data structure more suitable to use when facing different kinds of problems. The most commonly used types of trees are binary trees and heaps.
Binary trees
Binary trees are a type of tree in which each node has a maximum of two children.
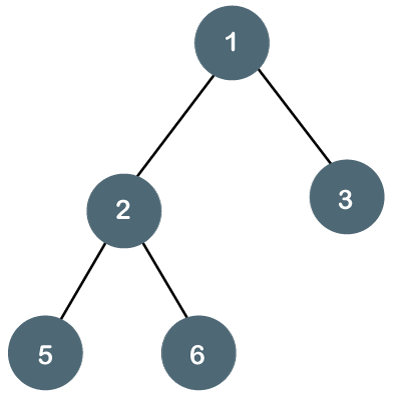
A binary tree
One key situation in which binary trees are really useful is in searching. And for searching, a certain type of binary tree is used, called binary search trees (BSTs).
BSTs are just like binary trees but information within them is ordered in a way that makes them a suitable data structure for searching.
In BST, values are ordered so that each node that descends to the left side of its parent must have a value less than its parent, and each node that descends to the right side of its parent must have a value bigger than its parent.

A binary search tree
This order in its values make this data structure great for searching, since on every level of the tree we can identify if the value being looked for is greater or less than the parent node, and from that comparison progressively discard roughly half of the data until we reach our value.
When inserting or deleting values, the algorithm will follow the following steps:
Check if there's a root node.
If there is, check if the value to add/delete is greater or smaller than the node.
If it is smaller, check if there is a node to the left and repeat the previous operation. If there's not, add/remove the node in that position.
If it is greater, check if there is a node to the right and repeat the previous operation. If there's not, add/remove the node in that position.
Searching in BSTs is very similar, only instead of adding/deleting values we check the nodes for equality with the value we're looking for.
The big O complexity of these operations is logarithmic (log(n)). But it's important to recognize that for this complexity to be achieved, the tree must have a balanced structure so that in each search step, approximately half of the data can be "discarded". If more values are stored to one side or another of three, the efficiency of the data structure is affected.
An implementation of a BST might look like this:
// We create a class for each node within the tree
class Node{
// Each node has three properties, its value, a pointer that indicates the node to its left and a pointer that indicates the node to its right
constructor(value){
this.value = value
this.left = null
this.right = null
}
}
// We create a class for the BST
class BinarySearchTree {
// The tree has only one property which is its root node
constructor(){
this.root = null
}
// The insert method takes a value as parameter and inserts the value in its corresponding place within the tree
insert(value){
const newNode = new Node(value)
if(this.root === null){
this.root = newNode
return this
}
let current = this.root
while(true){
if(value === current.value) return undefined
if(value < current.value){
if(current.left === null){
current.left = newNode
return this
}
current = current.left
} else {
if(current.right === null){
current.right = newNode
return this
}
current = current.right
}
}
}
// The find method takes a value as parameter and iterates through the tree looking for that value
// If the value is found, it returns the corresponding node and if it's not, it returns undefined
find(value){
if(this.root === null) return false
let current = this.root,
found = false
while(current && !found){
if(value < current.value){
current = current.left
} else if(value > current.value){
current = current.right
} else {
found = true
}
}
if(!found) return undefined
return current
}
// The contains method takes a value as parameter and returns true if the value is found within the tree
contains(value){
if(this.root === null) return false
let current = this.root,
found = false
while(current && !found){
if(value < current.value){
current = current.left
} else if(value > current.value){
current = current.right
} else {
return true
}
}
return false
}
}
Heaps
Heaps are another type of tree that have some particular rules. There are two main types of heaps, MaxHeaps and MinHeaps. In MaxHeaps, parent nodes are always greater than its children, and in MinHeaps, parent nodes are always smaller than its children.
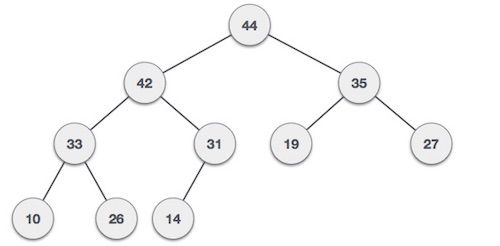
A max heap
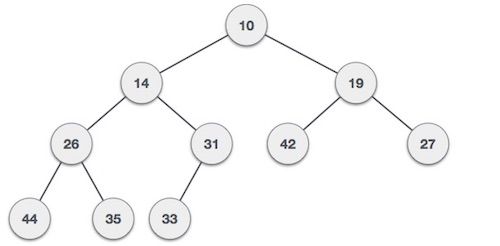
A min heap
In this data structure there're no guarantees between siblings, meaning that nodes at the same "level" don't follow any rule besides being higher/lower than their parent.
Also, heaps are as compact as possible, meaning each level contains all the nodes it can contain with no empty spaces, and new children are put into the left spaces of the tree first.
Heaps, and in particular binary heaps, are frequently used to implement priority queues, which at the same time are frequently used in well-known algorithms such as Dijkstra's path-finding algorithm.
Priority queues are a type of data structure in which each element has an associated priority and elements with a higher priority are presented first.
Graphs
Graphs are a data structure formed by a group of nodes and certain connections between those nodes. Unlike trees, graphs don't have root and leaf nodes, nor a "head" or a "tail". Different nodes are connected to each other and there's no implicit parent-child connection between them.
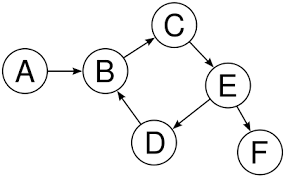
A graph
Graphs are data structures often useful for:
Social networks
Geolocalizaton
Recommendation systems
Graphs can be classified into different types according to the characteristics of the connections between nodes:
Undirected and directed graphs
We say a graph is undirected if there's no implicit direction in the connections between nodes.
If we take the following example image, you can see that there's no direction in the connection between node 2 and node 3. The connection goes both ways, meaning you can traverse the data structure from node 2 to node 3, and from node 3 to node 2. Undirected means the connections between nodes can be used both ways.

An undirected graph
And as you may have guessed, directed graphs are the exact opposite. Let's reuse the previous example image, and see that here there's an implicit direction in the connections between nodes.
In this particular graph, you could traverse from node A to node B, but you can't go from node B to A.

A directed graph
Weighted and unweighted graphs
We say a graph is weighted if the connections between nodes have an assigned weight. In this case, weight just means a value that is assigned to a specific connection. It's information about the connection itself, not about the nodes.
Following this example, we can see the connection between nodes 0 and 4, has a weight of 7. And the connection between nodes 3 and 1 has a weight of 4.

A weighted graph
To understand the use of weighted graphs, imagine if you wanted to represent a map with many different locations, and give the user information about how long it might take them to go from one place to another.
A weighted graph would be perfect for this, as you could use each node to save information about the location, the connections could represent the available roads between each place, and the weights would represent the physical distance from one place to another.
Weighted graphs are heavily used in geolocation systems
And as you may have guessed once again, unweighted graphs are the ones where connections between nodes have no assigned weights. So there's no particular information about the connections between nodes, only about the nodes themselves.
How to represent graphs
When coding graphs, there're two main methods we can use: an adjacency matrix and an adjacency list. Let's explain how both work and see their pros and cons.
An adjacency matrix is a two dimensional structure that represents the nodes in our graph and the connections between them.
If we use this example...
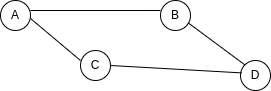
Our adjacency matrix would look like this:
| - | A | B | C | D |
| A | 0 | 1 | 1 | 0 |
| B | 1 | 0 | 0 | 1 |
| C | 1 | 0 | 0 | 1 |
| D | 0 | 1 | 1 | 0 |
You can see that the matrix is like table, where columns and rows represent the nodes in our graph, and the value of the cells represent the connections between nodes. If the cell is 1, there's a connection between the row and the column, and if it's 0, there's not.
The table could be easily replicated using a two dimensional array:
[
[0, 1, 1, 0]
[1, 0, 0, 1]
[1, 0, 0, 1]
[0, 1, 1, 0]
]
On the other hand, an adjacency list can be thought as a key-value pair structure where keys represent each node on our graph and the values are the connections that that particular node has.
Using the same example graph, our adjacency list could be represented with this object:
{
A: ["B", "C"],
B: ["A", "D"],
C: ["A", "D"],
D: ["B", "C"],
}
You can see that for each node we have a key, and we store all the node's connections within an array.
So what's the difference between adjacency matrices and lists? Well, lists tend to be more efficient when it comes to adding or removing nodes, while matrices are more efficient when querying for specific connections between nodes.
To see this, imagine we wanted to add a new node to our graph:
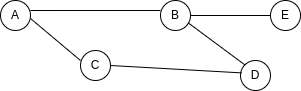
To represent this in a matrix, we would need to add a whole new column and a whole new row:
| - | A | B | C | D | E |
| A | 0 | 1 | 1 | 0 | 0 |
| B | 1 | 0 | 0 | 1 | 1 |
| C | 1 | 0 | 0 | 1 | 0 |
| D | 0 | 1 | 1 | 0 | 0 |
| E | 0 | 1 | 0 | 0 | 0 |
While to do the same in a list, adding a value to B connections and a key-value pair to represent E is enough:
{
A: ["B", "C"],
B: ["A", "D", "E"],
C: ["A", "D"],
D: ["B", "C"],
E: ["B"],
}
Now imagine we want to verify if there's an existing connection between node B and E. Checking that in a matrix is dead easy, as we know exactly the position in the matrix that represents that connection.
| - | A | B | C | D | E |
| A | 0 | 1 | 1 | 0 | 0 |
| B | 1 | 0 | 0 | 1 | 1 |
| C | 1 | 0 | 0 | 1 | 0 |
| D | 0 | 1 | 1 | 0 | 0 |
| E | 0 | 1 | 0 | 0 | 0 |
But in a list, we don't have that information we would need to iterate all over the array that represents B connections and see what's in there. So you can see there are pros and cons for each approach.
A full implementation of a graph using an adjacency list might look like this. To keep things simple, we'll represent an undirected unweighted graph.
// We create a class for the graph
class Graph{
// The graph has only one property which is the adjacency list
constructor() {
this.adjacencyList = {}
}
// The addNode method takes a node value as parameter and adds it as a key to the adjacencyList if it wasn't previously present
addNode(node) {
if (!this.adjacencyList[node]) this.adjacencyList[node] = []
}
// The addConnection takes two nodes as parameters, and it adds each node to the other's array of connections.
addConnection(node1,node2) {
this.adjacencyList[node1].push(node2)
this.adjacencyList[node2].push(node1)
}
// The removeConnection takes two nodes as parameters, and it removes each node from the other's array of connections.
removeConnection(node1,node2) {
this.adjacencyList[node1] = this.adjacencyList[node1].filter(v => v !== node2)
this.adjacencyList[node2] = this.adjacencyList[node2].filter(v => v !== node1)
}
// The removeNode method takes a node value as parameter. It removes all connections to that node present in the graph and then deletes the node key from the adj list.
removeNode(node){
while(this.adjacencyList[node].length) {
const adjacentNode = this.adjacencyList[node].pop()
this.removeConnection(node, adjacentNode)
}
delete this.adjacencyList[node]
}
}
const Argentina = new Graph()
Argentina.addNode("Buenos Aires")
Argentina.addNode("Santa fe")
Argentina.addNode("Córdoba")
Argentina.addNode("Mendoza")
Argentina.addConnection("Buenos Aires", "Córdoba")
Argentina.addConnection("Buenos Aires", "Mendoza")
Argentina.addConnection("Santa fe", "Córdoba")
console.log(Argentina)
// Graph {
// adjacencyList: {
// 'Buenos Aires': [ 'Córdoba', 'Mendoza' ],
// 'Santa fe': [ 'Córdoba' ],
// 'Córdoba': [ 'Buenos Aires', 'Santa fe' ],
// Mendoza: [ 'Buenos Aires' ]
// }
// }
Roundup
That's it, everyone. In this article we've introduced the main data structures used in computer science and software development. These structures are the base of most of the programs we use in every day life, so it's really good knowledge to have.
Even though this topic may feel a bit abstract and intimidating at first, I believe we can understand it better by just thinking data structures as ways in which we organize data to better achieve certain tasks.
As always, I hope you enjoyed the article and learned something new. If you want, you can also follow me on LinkedIn or Twitter.
See you later!


