A regression problem is a common type of supervised learning problem in Machine Learning. The end goal is to predict quantitative values – for example, continuous values such as the price of a car, the weight of a dog, and so on.
But to be sure that your model is doing well in its predictions, you need to evaluate the model.
There are some evaluation metrics that can help you determine whether the model’s predictions are accurate to a certain level of performance.
In this tutorial, you will learn the top evaluation metrics for regression problems, as well as when to use each of them. Without further ado let’s get started.
What are Residuals?
Before we get into the top evaluation metrics, you need to understand what "residual" means when you're evaluating a regression model.
It is not ideal or possible for a model to accurately predict the value of a continuous variable in a regression problem. A regression model can only predict values that are lower or higher than the actual value. As a result, the only way to determine the model’s accuracy is through residuals.
Residuals are the difference between the actual and predicted values. You can think of residuals as being a distance. So, the closer the residual is to zero, the better our model performs in making its predictions.
Here's the formula for calculating residuals:
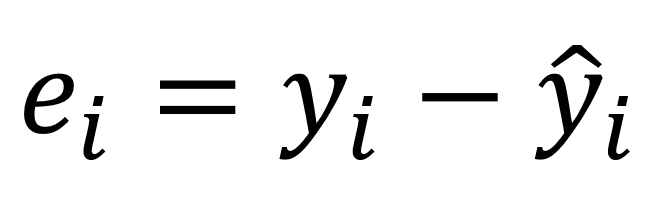
In the above formula:
ei -- stands for the residual value.
yi -- stands for the actual value.
y^i -- stands for the predicted value.
So say, for instance, that the actual value in the dataset is 5 and the predicted value is 8. The residual value will be -3.
Top Evaluation Metrics for Regression Problems
The top evaluation metrics you need to know for regression problems include:
R2 Score
The R2 score (pronounced R-Squared Score) is a statistical measure that tells us how well our model is making all its predictions on a scale of zero to one.
As mentioned above, it's not ideal for a model to predict the actual values in a regression problem (as opposed to a classification problem that has discrete levels of value).
But we can use the R2 score to determine the accuracy of our model in terms of distance or residual. You can calculate the R2 score using the formula below:

When to Use the R2 Score
You can use the R2 score to get the accuracy of your model on a percentage scale, that is 0–100, just like in a classification model.
Let’s go over how to implement the R2 score in Python. So we have a small dataset that contains the actual values and the predictions.

To implement the R2 score in Python we'll leverage the Scikit-Learn evaluation metrics library.
from sklearn.metrics import r2_score
score = r2_score(data["Actual Value"], data["Preds"])
print("The accuracy of our model is {}%".format(round(score, 2) *100))
The r2_score requires two parameters – the actual value and the predicted values in which we have passed to it above. The result from the metrics is this:

So we can say that our model predicted those values with 82% accuracy.
Mean Absolute Error (MAE)
The MAE is simply defined as the sum of all the distances/residual s(the difference between the actual and predicted value) divided by the total number of points in the dataset.
It is the absolute average distance of our model prediction.
You can calculate the MAE using the following formula:
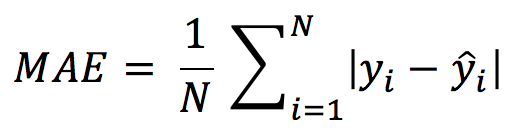
We can see that the above formula has two pipelines represented by the absolute symbol. The absolute symbol makes sure that the negative residual (which may be a result where the predicted value is greater than the actual value) is converted to positive so that it doesn’t cancel out other positive residuals.
When to Use MAE
If you want to know the model’s average absolute distance when making a prediction, you can use MAE. In other words, you want to know how close the predictions are to the actual model on average.
Just keep in mind that low MAE values indicate that the model is correctly predicting. Larger MAE values indicate that the model is poor at prediction.
Let’s now see how to implement MAE in Python. We will be working with the previous dataset we used to find the r2_score.

To implement the MAE in Python we'll leverage the Scikit-Learn evaluation metrics library.
from sklearn.metrics import mean_absolute_error
score = mean_absolute_error(data["Actual Value"], data["Preds"])
print("The Mean Absolute Error of our Model is {}".format(round(score, 2)))
MAE also requires two parameters, the actual value and the predicted value.

Root Mean Squared Error (RMSE)
Another commonly used metric is the root mean squared error, which is the square root of the average squared distance (difference between actual and predicted value).
RMSE is defined as the square root of all the squares of the distance divided by the total number of points.

RMSE functions similarly to MAE (that is, you use it to determine how close the prediction is to the actual value on average), but with a minor difference.
You use the RMSE to determine whether there are any large errors or distances that could be caused if the model overestimated the prediction (that is the model predicted values that were significantly higher than the actual value) or underestimated the predictions (that is, predicted values less than actual prediction).
When to Use RMSE
If you are concerned about large errors, RMSE is a good metric to use. If the model overestimated or underestimated some points in the prediction (because the residual will be square, resulting in a large error), you should use RMSE.
RMSE is a popular evaluation metric for regression problems because it not only calculates how close the prediction is to the actual value on average, but it also indicates the effect of large errors. Large errors will have an impact on the RMSE result.
Let’s take a look at how you can implement RMSE in Python.

The Scikit-learn evaluation metric library has no RMSE metric, but it does include the mean squared error method. The square root of the mean squared error is referred to as RMSE.
To get the RMSE, we can use the Numpy square root method to find the square root of mean squared error, and the result obtained is our RMSE.
from sklearn.metrics import mean_squared_error
import numpy as np
score = np.sqrt(mean_absolute_error(data["Actual Value"], data["Preds"]))
print("The Mean Absolute Error of our Model is {}".format(round(score, 2)))

We can see that the RMSE value is larger than the MAE. This is a result of some large errors in the dataset.
Conclusion and Learning More
In this tutorial you’ve learned some of the top evaluation metrics for regression problems that you will use on a daily basis.
Thank you for reading. Here are some helpful resources I also included below.
MAE and RMSE — Which Metric is Better? | by JJ | Human in a Machine World | Medium

