By Alaina Kafkes
How a linguistic breakthrough ended up in code
Regular expressions inspire fear in new and experienced programmers alike. When I first saw a regular expression — often abbreviated as “regex” — I remember feeling dizzy from looking at the litany of parentheses, asterisks, letters, and numbers. Regular expressions seemed nonsensical, impenetrable.
I expected regular expressions to crop up again in my upper-level computer science coursework — maybe by then I’d finally feel ready to tackle them — but I encountered them in an introductory class that I had put off until my senior year. The purpose of this course was to draw students who had never written a line of code into CS by introducing them to concepts like cryptography, human-computer interaction, machine learning — you know, only the latest and greatest of tech buzzwords.
I didn’t attend more than a handful of lectures, but one of the assignments stuck with me. I had to write an essay about a famous computer scientist or academic whose work impacted computer science. I chose Noam Chomsky.
Little did I know that learning about Chomsky would drag me down a rabbit hole back to regular expressions, and then magically cast regular expressions into something that fascinated me. What enchanted me about regular expressions was the homonymous linguistic concept that powered them.
I hope to spellbind you, too, with the linguistics behind regular expressions, a a backstory unknown to most programmers. Though I won’t teach you how to use regular expressions in any particular programming language, I hope that my linguistic introduction will inspire you to dive deeper into how regular expressions work in your programming language of choice.
To begin, let’s return to Chomsky: what does he have to do with regular expressions? Hell, what does he even have to do with computer science?
A Computer Scientist By Accident
Wikipedia christens Noam Chomsky as a linguist, philosopher, cognitive scientist, historian, social critic, and political activist, but not as a computer scientist. Because he is so highly regarded in all of these fields, his indirect contributions to the field of computer science often fall by the wayside.
The more I researched Chomsky’s academic work, the more accidental Chomsky’s foray into computing seemed. This affirmed my belief that all fields — even those that appear disparate from computer science — have something to offer to computing and the tech industry.
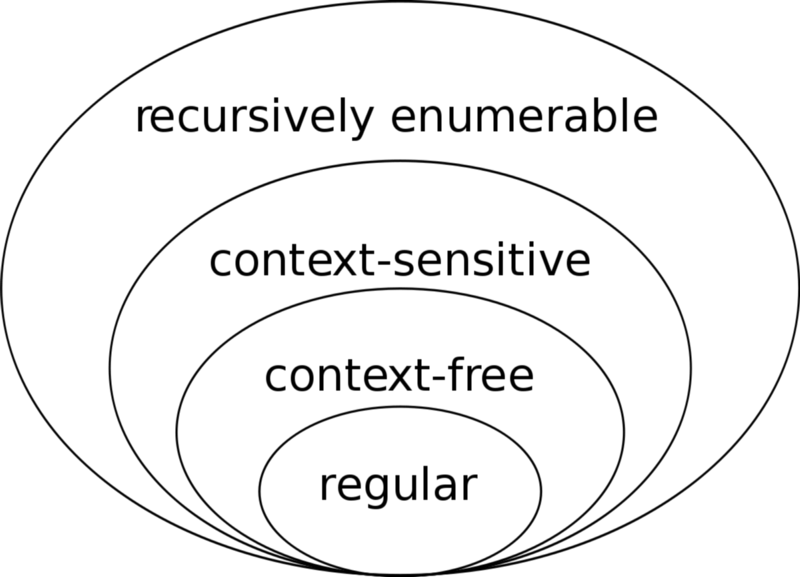
His contributions to the field of linguistics in particular exemplify the impact of interdisciplinary research on computer science. The Chomsky hierarchy transformed the code that computer scientists, software engineers, and hobbyists write today.
Yes, it was this hierarchy that brought regular expressions to computer science. But, before we can understand the jump from Chomsky to regular expressions, I’ll outline the Chomsky hierarchy.
Linguistic Law & Order
The Chomsky hierarchy is an ordering of formal grammars — think syntactic rules for formal languages — such that each grammar exists as a proper subset of the grammars above it in the hierarchy. Some formal languages have stricter grammars than others, so Chomsky sought to organize formal grammars into his eponymous hierarchy.
I briefly mentioned that formal grammars are syntactic rules: rules that give all possible valid phrases for a given formal language. Grammars provide the rules that build languages. In linguist-speak, a language’s formal grammar provides a framework with which nonterminals (input or intermediate string values) can be converted into terminals (output string values).
To elucidate this new vocabulary, I’ll walk through an example of converting a set of nonterminals into terminals using a made-up formal grammar. Let’s say that our pretend formal language, Parseltongue, has the following formal grammar:
- Terminals: {s, sh, ss}
- Nonterminals: {snake, I, am}
- Production rules: {I → sh, am → s, snake → ss}
Using the production rules, I can convert the input sentence “I am snake” into “sh s ss.” This conversion happens piece by piece: “I am snake” → “sh am snake” → “sh s snake” → “sh s ss.”
As my Parseltongue example illustrates, formal grammars parse strings of nonterminals into terminal-only strings — grammatically correct phrases. But formal grammars act not only as generators of a language, but also recognizers of whether a string fits the formal grammar. Whereas the example string “I am a snake” can be fully converted into terminals, the string “I am not a snake” cannot be written in Parseltongue because the nonterminal “not” cannot be translated into a Parseltongue terminal.
To re-emphasize something I stated earlier: formal grammars generate formal languages. That means that, by creating a hierarchy of formal grammars, Chomsky also categorized languages themselves.
With that sobering introduction, let’s look at the four formal grammars in Chomsky’s hierarchy. From most to least strict, they are:
- Regular grammars, which retain no past state knowledge from input string to output string
- Context-free grammars, which retain only recent state knowledge from input string to output string
- Context-sensitive grammars, which keep all past state knowledge from input string to output string
- Unrestricted (or recursively enumerable) grammars, which have all state knowledge and thus can create every output string imaginable from a given input string
What is this “state knowledge” that I speak of? Think of knowledge in terms of scope. Regular grammars, for example, have no knowledge of the string’s past states in their “scope” in the process of converting an input string into an output string. This suggests that once the grammar makes an individual conversion of nonterminal to terminal (plus a series of zero or more nonterminals), the grammar “forgets” the previous state of the string.
On the other hand, unrestricted grammars hold onto every possible state of the string-in-translation. Context-free and context-sensitive grammars fall somewhere in the middle.
If you’re looking for a more detailed explanation of the grammars in the Chomsky hierarchy, you’ll have to take a peek at automata theory. I’ll focus on the grammar that brings us back to regular expressions, fittingly called the regular grammar.
On the Regular Expressions
Regular expressions and regular grammars are equivalent. They communicate the same set of syntactic rules, albeit using different formalisms, and both produce the same regular languages.
In linguistics, a regular expression is recursively defined as follows:
- The empty set is a regular expression.
- The empty string is a regular expression.
- For any character x in the input alphabet, x is a regular expression that produces the regular language {x}.
- Alternation: If x and y are regular expressions, then x | y is a regular expression. For example, the regular expression
0|1produces the regular language{0,1}. - Concatenation: If x and y are regular expressions, then x • y is a regular expression. For example, the regular expression
0•1produces the regular language{01}. - Repetition (also known as Kleene star): If x and y are regular expressions, then x is a regular expression. For example, the regular language `0•1
produces the regular language{0, 01, 011, 0111, ...}`, ad infinitum.
A regular grammar is composed of rules like those of Parseltongue. Just as a regular grammar can be utilized to parse an input string into an output string, a regular expression converts strings quite similarly. You can see examples of this parsing for the alternation, concatenation, and repetition operations — or, to use my prior analogy, rules — that regular expressions adopt.
Let’s return to our friend Noam Chomsky for a moment. According to his hierarchy of grammars, regular grammars retain no information about intermediate steps in converting from an input string to an output string. What does this tell us about regular expressions?
The “forgetfulness” of regular grammars implies that translations in one part of the string do not impact how the other nonterminals in the string are translated in future steps. There is no coordination between different parts of the string in the creation of the output string.
Looking at the linguistics behind regular grammars gives us insight into why programmers first brought regular expressions into code. Although I’ve only discussed formal grammars as generators and recognizers of language, the fact that regular grammars convert input string to output string piece by piece makes them pattern-matchers. In programming, regular expressions use production rules to convert an input string — a pattern — into a regular language — a set of strings that match that pattern.
But I would have never written this blog post if programming language creators implemented regular expressions exactly as they are defined in the field of linguistics. Computational regular expressions are a far cry from their linguistic precursor, but the linguistic regular expressions that I covered provide a useful framework for understanding regular expressions in code.
Two Regular Expressions, Both Alike in Dignity
Hereafter, I will use the term regular expression to mean a linguistic regular expression and the term regex to signify a programmatic regular expression. In the wild, both linguistic and programmatic regular expressions are referred to as “regular expressions” even though they are quite different from one another — how confusing!
The difference between regular expressions and regexes stems from how they are used. Regular expressions — or regular grammars — are part of formal language theory, which exists to describe shared elements of natural languages — languages that evolved over time without human premeditation. Linguists use regular expressions for theoretical purposes, like the categorization of formal grammars in the Chomsky hierarchy. Regular expressions help linguists understand the languages that humans speak.
Regexes, on the other hand, are utilized by everyday programmers who want to search for strings that match a given pattern. While regular expressions are theoretical, regexes are pragmatic. Programming languages are formal languages: languages designed by people (here, programmers) for specific purposes. As you might imagine, programming language creators augmented the functionality of regexes in code. Let’s examine these enhancements.
Remember that regular expressions have three operations: alternation, concatenation, and repetition. I’m no regex expert — regexpert? — but all it takes is a peek at the regular expression Wikipedia page to notice that regexes implement more than just three operations.
For example, using POSIX regex syntax, the pattern .ork matches all four-character strings that end with the three characters “ork.” That period is more powerful than simple alternation, concatenation, and repetition, right?
Nope. Truth be told, even the fanciest of regex metacharacters — characters that invoke a regex operation — derive from regular expression operations. Assuming that the twenty-six lowercase letters of the alphabet are the only characters in the regular grammar, the regex pattern .ork could be written using only regular expression operations as [a|b|c|...|z]ork.
Though the sheer volume of metacharacters suggests that regex has a more powerful set of operations than regular expressions themselves, metacharacters are merely shortcuts for various permutations of the operations that define regular expressions. Regex metacharacters provide a programmer-friendly abstraction for common combinations of alternation, concatenation, and repetition.
So far, I’ve portrayed regexes as regular expressions with amazing shortcuts and clear-cut use cases. However, as you may recall from Chomsky’s hierarchy, regular grammars have the strictest rules and no scope. Luckily, regexes have a little more leeway than their linguistic precursor, thereby bestowing them with more practical power.
Breaking the Regular Grammar Rules
Recall that, according to the the Chomsky hierarchy, regular grammars retain no knowledge in converting an input string to an output string. Since regular expressions are equivalent to regular grammars, this means that regular expressions also have no memory of the intermediate states of a string as it changed from input to output. It also means that translating a nonterminal in one part of a regular expressions has no bearing on the translation of a nonterminal in another part of the expression.
For regexes, it’s a different story. Regexes violate this key regular grammar characteristic by supporting the ability to backreference. Backreferencing allows the programmer to parenthetically separate a subsection of a regular expression and refer to it using a metacharacter. To give an example, the pattern (la)\1 matches “lala” by employing the \1 metacharacter to repeat the search for “la.”
Because different parts of the string cannot influence one another in regular expressions, backreferencing gives regexes a lot more power than their predecessor. More importantly, backreferencing facilitates practical uses of regex such as searching for typos in which the same word was accidentally typed twice in a row. Pragmatism gives insight into why regular expressions were tweaked to create regexes in programming.
Another feature that increases the functionality of regex is the ability to alter the greediness of the matching. Different quantifiers — categories of regex patterns — can look similar but match drastically different parts of a string. A greedy quantifier () will attempt to match as much of the string as possible, whereas a reluctant quantifier (?) will try to match the minimum amount of characters in the string. Given the string “abcorgi,” the pattern `.corgiwould match the entire string but the pattern.?corgi` would only match “bcorgi.”
A possessive quantifier (+) also attempts to match as much of the string as possible, but, unlike the greedy quantifier, it will not backtrack to previous characters in the string in order to find the largest possible match. Given the string “abcorgi,” the patterns .*corgi and .+corgi would match the entire string. Though possessive and greedy qualifiers will often produce the same result, possessive qualifiers tend to be more efficient because they avoid backtracking.
Because quantifiers are metacharacters, they can technically be built from alternation, concatenation, and repetition: the three operations of regular expressions. However, quantifiers create a simple abstraction that allows programmers to quickly specify what type of match they would like.
Conclusion & Further Reading
What a journey we’ve undertaken! We learned about Chomsky and his eponymous hierarchy, then dove deeper into regular grammars. From regular grammars, we explored the linguistic definition of a regular expression. Finally, we used the differences between regular expressions and regexes to motivate how programmers use regex today.
Although I trace the history of regular expressions from Chomsky to modern programming languages, this blog post is not the end of the regex story. If you’d like to learn more about linguistic and computational regular expressions, I have some motivating questions for you.
- What is automata theory and how does it relate to the Chomsky hierarchy?
- How are regex implemented? What are the tradeoffs of various regex algorithms?
- When is it appropriate to use regexes instead of built-in string match and manipulation libraries?
I also have a list of resources that I used to study up on the linguistic and computational elements of regular expressions. Happy regex-ing!
- Regular-Expressions.info
- Wikipedia: Regular Expressions
- StackOverflow: Chomsky Hierarchy in plain English
- Introduction to Automata Theory, Languages, and Computation by Hopcroft et al.
- StackOverflow: Difference between regular expression and grammar in automata
- How to Think like a Computer Scientist: Formal and Natural Languages
- Oracle’s Java Tutorials: Quantifiers
- StackOverflow: Compare regex in programming languages with regular expression from automata/formal language
- Quora: How are regular expressions implemented?
Enjoy what you read? Spread the love by liking and sharing this piece. Have thoughts or questions? Reach out to me on Twitter or in the comments below. Thank you Miles Hinson for proofreading this piece!