By Alexander Arobelidze
At times, in everyday situations, we may face the task of having to figure the square root of a number. What if there is no calculator or a smartphone handy? Can we use an old fashioned paper and pencil to do it in a long division style?
Yes we can, and there are several different methods. Some are more complex than others. Some provide more accurate results.
The one I want to share with you is one of them. To make this article more reader friendly, each step comes with illustrations.
STEP 1: Separate The Digits Into Pairs

To begin, let's organize the workspace. We will divide the space into three parts. Then, let’s separate the number’s digits into pairs moving from right to left.
For example, the number 7,469.17 becomes 74 69. 17. Or in the case of a number with an odd amount of digits such as 19,036, we will start with 1 90 36.
In our case here, 2,025 becomes 20 25.
STEP 2: Find The Largest Integer
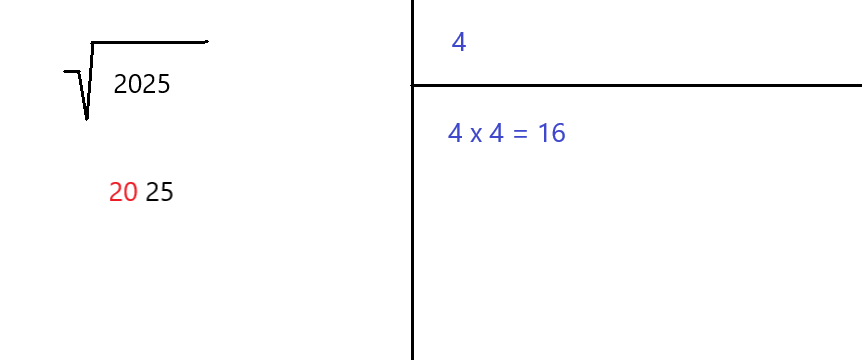
As the next step, we need to find the largest integer (i) whose square is less than or equal to the leftmost number.
In our current example the leftmost number is 20. Since 4² = 16 <= 20 and 5² = 25 > 20, the integer in question is 4. Let’s deposit 4 to the top-right corner and 4² = 16 to the bottom right one.
STEP 3: Now Subtract That Integer
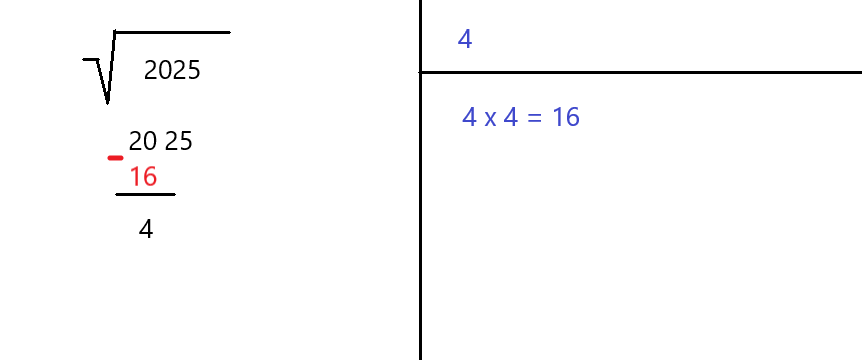
Now we need to subtract the square of that integer (which equals 16) from the leftmost number (which equals 20). The result equals 4 and we will write it as shown above.
STEP 4: Let's Move To The Next Pair
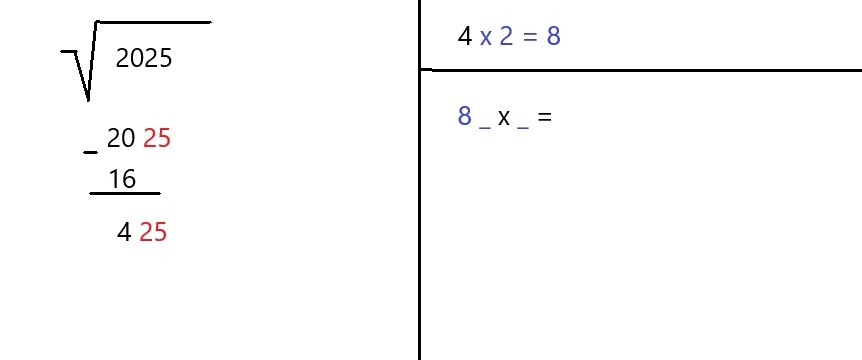
Next, let's move down the next pair in our number (which is 25). We write it next to the subtracted value already there (which is 4).
Now multiply the number in the top right corner (which is also 4) by 2. This results in 8 and we write it in the bottom right corner followed by x =
STEP 5: Find The Right Match
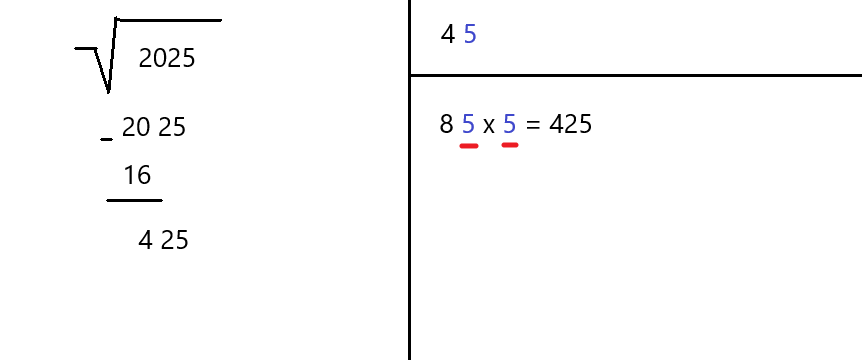
Time to fill in each blank space with the same integer (i). It must be the largest possible integer that allows the product to be less than or equal the number on the left.
For example, if we choose the number 6, the first number becomes 86 (8 and 6) and we must also multiply it by 6. The result 516 is greater than 425, so we go lower and try 5. The number 8 and the number 5 give us 85. 85 times 5 results in 425, which is exactly what we need.
Write 5 next to 4 in the top right corner. It is the second digit in the root.
STEP 6: Subtract Again

Subtract the product we calculated (which is 425) from the current number on the left (also 425). The result is zero, which means the task is complete.
Note: I chose a perfect square (2025 = 45 x 45) on purpose. This way I could show the rules for solving square root problems.
In reality, numbers consist of many digits, including the ones after the decimal point. In that case we repeat steps 4, 5 and 6 until we reach any accuracy we want.
The next example explains what I mean.
EXAMPLE: We dig deeper...
This time the number consists of an odd number of digits including the ones after the decimal point.

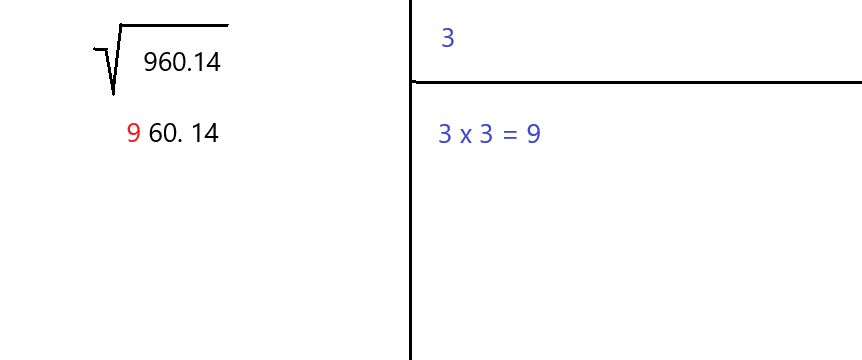

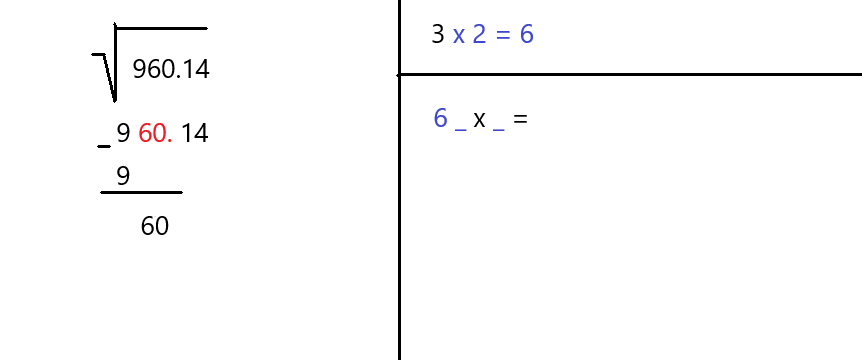
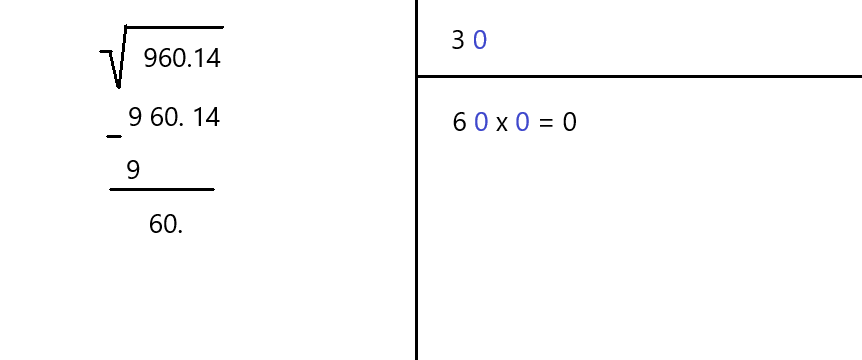
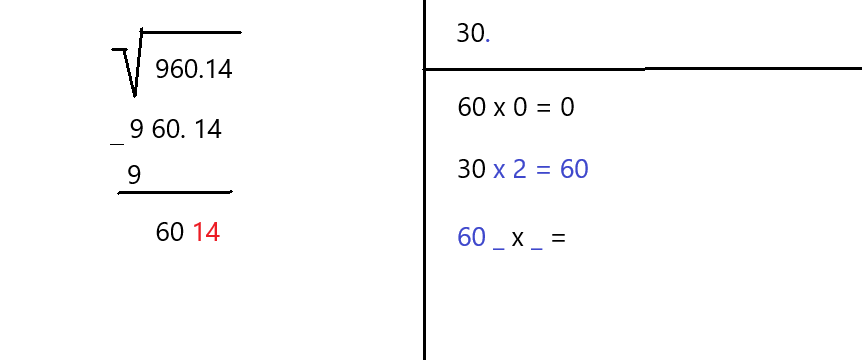
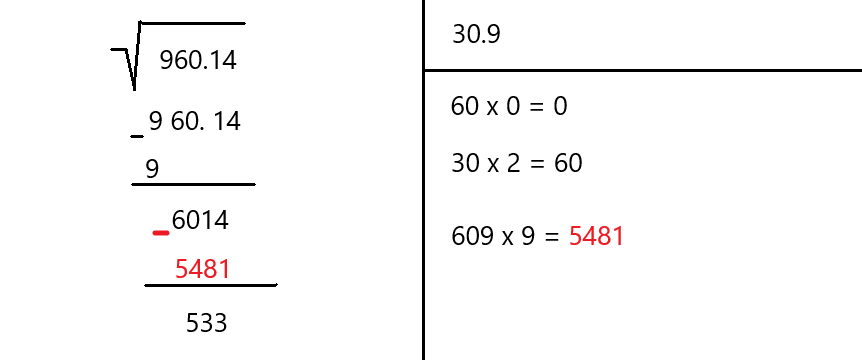
As we saw in this example, the process can repeat several times over to reach a desired level of accuracy.
