By Elena Nisioti
Artificial Intelligence (AI) is full of questions that cannot be answered and answers that cannot be assigned to the correct questions. In the past, it paid for its persistence to wrong practices with periods of stagnation, known as AI winters. The calendar of AI, however, has just reached spring, and the applications are flourishing.
Yet, there is a branch of AI that has long been neglected. The talk is about reinforcement learning, that has recently exhibited impressive results on games like AlphaGo and Atari. But let’s be honest: these were not reinforcement learning wins. What got deeper in these cases was the deep neural networks, and not our understanding of reinforcement learning, which maintains the depth it achieved decades ago.
Even worse is the case of reinforcement learning when applied to real life problems. If training a robot to balance on a rope sounds hard, try training a team of robots to win a football game, or a team of drones to monitor a moving target.
Before we lose the branch, or even worse the tree, we must sharpen our understanding of these applications. Game theory is the most common approach to studying teams of players that share a common goal. It can lend us tools to guide learning algorithms in these settings.
But let’s see why the common approach is not a common sense approach.
To kill an error is as good a service as, and sometimes even better than, the establishing of a new truth or fact. — Charles Darwin
First, let’s dirty our hands with some terminology and basics of these areas.
Game theory
Some useful terms
- Game: like games in popular understanding, it can be any setting where players take actions and its outcome will depend on them.
- Player: a strategic decision-maker within a game.
- Strategy: a complete plan of actions a player will take, given the set of circumstances that might arise within the game.
- Payoff: the gain a player receives from arriving at a particular outcome of a game.
- Equilibrium: the point in a game where both players have made their decisions and an outcome is reached.
- Nash equilibrium: an equilibrium in which no player can gain by changing their own strategy if the strategies of the other players remain unchanged.
- Dominant strategy: occurs when one strategy is better than another strategy for one player, no matter how that player’s opponents may play.
Prisoner’s dilemma
This is probably the most famous game in the literature. The figure below presents its payoff matrix. Now, a payoff matrix is worth a thousand words. It is sufficient, to an experienced eye, to provide all the information necessary to describe a game. But let’s be a bit less laconic.
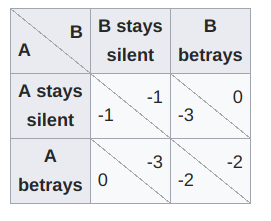
The police arrest two criminals, criminal A and criminal B. Although quite notorious, the criminals cannot be imprisoned for the crime under investigation due to lack of evidence. But they can be held for lesser charges.
The length of their imprisonment will depend on what they will say in the interrogation room, which gives rise to the game. Each criminal (player) is given the chance to either stay silent or snitch on the other criminal (player). The payoff matrix depicts how many years each player will be imprisoned depending on the outcome. For example, if player A stays silent and player B snitches on them, player A will serve 3 years (-3) and player B will serve none (0).
If you reviews the payoff matrix carefully, you will find out that the logical action of a player is to betray the other person or, in game-theoretic terms, betraying is the dominant strategy. This will lead to the Nash equilibrium of the game, where each player has a payoff of -2.
Does something feel odd? Yes, or at least it should. If both players somehow agreed to remain silent they would both get a higher reward of -1. Prisoner’s dilemma is an example of a game where rationality leads to a worse result than cooperation would.
Some historical remarks
Game theory originated in economics, but is today an interdisciplinary area of study. Its father, John von Neumann (you will notice that Johns have serious career prospects in this area), was the first to give a strict formulation to the common notion of a game. He restricted his studies to games of two players, as they were easier to analyze.
He then co-authored a book with Oskar Morgenstern, which laid the foundations for expected utility theory and shaped the course of game theory. Around that time, John Nash introduced the concept of Nash equilibria, which helps describe the outcome of a game.
Reinforcement learning
It did not take long to realize how vast the applications of game theory can be. From games to biology, philosophy and, wait for it, artificial intelligence. Game theory is nowadays closely related to settings where multiple players learn through reinforcement, an area called multi-agent reinforcement learning. Examples of applications in this case are teams of robots, where each player has to learn how to behave in favor of its team.
Some useful terms
- Agent: equivalent to a player.
- Reward: equivalent to a payoff.
- State: all the information necessary to describe the situation an agent is in.
- Action: equivalent of a move in a game.
- Policy: similar to a strategy, it defines the action an agent will make when in particular states
- Environment: everything the agent interacts with during learning.
Applications
Imagine the following scenario: a team of drones is unleashed into a forest in order to predict and locate fires early enough for the firefighters to respond. The drones are autonomous and must explore the forest, learn which conditions are likely to cause fire, and cooperate with each other, so that they cover wide areas of the forest using little battery and communication.
This application belongs to the area of environmental monitoring, where AI can lend its predictive skills to human intervention. In a technological world that is becoming increasingly complex and a physical world under threat, we can paraphrase Kipling’s quote to “Man could not be everywhere, and therefore he made drones.”
Decentralized architectures are another interesting application field. Technologies like the Internet of Things and Blockchain create immense networks. Information and processing is distributed in different physical entities, a trait that has been acknowledged to offer privacy, efficiency and democratization.
Regardless of whether you want to use sensors to minimize energy consumption in the households of a country, or replace the banking system, decentralized is the new sexy.
Making these networks smart, however, is challenging, as most of the AI algorithms we are proud of are data- and computation-hungry. Reinforcement learning algorithms can be employed for efficient data processing and rendering the network adaptive to changes in its environment. In this case, it is interesting, and to the benefit of overall efficiency, to study how the individual algorithms will cooperate.

Not just a game
Translating AI problems to simple games like the prisoner’s dilemma is tempting. This is a usual practice when testing new techniques, as it offers a computationally cheap and intuitive testbed. Nevertheless, it is important not to ignore the effect that the practical characteristics of the problem, such as noise, delays, and finite memory, have on the algorithm.
Perhaps the most misleading assumption in AI research is that of representing interaction with iterated static games. For example, an algorithm can apply the prisoner’s dilemma game every time it wants to make a decision, a formulation that assumes that the agent has not learned, or changed, along the way. But what about the effect learning will have on the behavior of the agent? Won’t interaction with others affect its strategy?
Research in this area has focused on evolution of cooperation and Robert Axelrod has studied optimal strategies that arise in the iterated version of prisoner’s dilemma. The tournaments that Axelrod organized revealed that strategies that adapt with time and interaction, even as simple as Tit-for-Tat may sound, are very effective.The AI community has recently investigated learning under the sequential prisoner’s dilemma, but research in this area is still in a premature state.
What differentiates multi-agent from single-agent learning is the increased complexity. Training one deep neural network is already enough of a pain, while adding new networks, as parts of the agents, makes the problem exponentially harder.
One less obvious, but more important concern, is the lack of theoretical properties for this kind of problem. Single-agent reinforcement learning is a well-understood area, as Richard Bellman and Christopher Watkins have offered the algorithms and proofs necessary to learn. In the multi-agent case, however, the proofs lose their validity.
Just to illustrate some of the mind-puzzling difficulties that arise: an agent executes a learning algorithm to learn how to react optimally to its environment. In our case, the environment includes the other agents, which also execute the learning algorithm. Thus, the algorithm has to consider the effect of its action before it acts.
The early concerns
The concerns start where game theory started: in economics. Let’s begin with some assumptions made when studying a system under classical game theory.
Rationality: generally in game theory, and in order to derive Nash equilibria, perfect rationality is assumed. This roughly means that agents always act for their own sake.
Complete information: each agent knows everything about the game, including the rules, what the other players know, and what their strategies are.
Common knowledge: there is common knowledge of a fact p in a group of agents when: all the agents know p, they all know that all agents know p, they all know that they all know that all agents know p, and so on ad infinitum. There are interesting puzzles, like the blue-eyed islanders, that describe the effect common knowledge has on a problem.
In 1986 Kenn Arrow expressed his reservations towards classical game theory.
In this paper, I want to disentangle some of the senses in which the hypothesis of rationality is used in economic theory. In particular, I want to stress that rationality is not a property of the individual alone, although it is usually presented that way. Rather, it gathers not only its force but also its very meaning from the social context in which it is embedded. It is most plausible under very ideal conditions. When these conditions cease to hold, the rationality assumptions become strained and possibly even self-contradictory.
If you find that Arrow is a bit harsh with classical game theory, how rational would you say your last purchases have been? Or, how much consciousness and effort did you put into your meal today?
But Arrow is not so much worried about the assumption of rationality. He is worried about the implications of it. For an agent to be rational, you need to provide them with all the information necessary to make their decisions. This calls for omniscient players, which is bad in two ways: first, it creates impractical requirements for information storing and processing of players. Second, game theory is no longer a game theory, as you can replace all players by a central ruler (and where is the fun in that?).
The value of information in this view is another point of interest. We have already discussed that possessing all the information is infeasible. But what about assuming players with limited knowledge? Would that help?
You may ask anyone involved in this area, but it suffices to say that optimization under uncertainty is tough. Yes, there still are the good-old Nash equilibria. The problem is that they are infinite. Game theory does not provide you with arguments to evaluate them. So, even if you reach one, you shouldn't make it such a big deal.
Reinforcement learning concerns
By this point you should suspect that AI applications are much more complicated than the examples classical game theory concerns itself with. Just to mention a few obstacles on the path of applying the Nash equilibrium approach in a robotic application: imagine being the captain of a team of robots playing football in RoboCup. How fast, strong, and intelligent are your players and your opponents? What strategies does the opponent team use? How should you reward your players? Is a goal the only reason for congratulating, or will applauding a good pass also improve the team’s behavior? Clearly, just being familiar with the rules of football will not win you the game.
If game theory has been raising debates for decades, if it has been founded on unrealistic assumptions and, for realistic tasks, if it offers complicated and little-understood solutions, why are we still going for it? Well, plainly enough, it’s the only thing we’ve got when it comes to group reasoning. If we actually understood how groups interact and cooperate to achieve their goals, psychology and politics would be much clearer.
Researchers in the area of multi-agent reinforcement learning either completely emit a discussion on the theoretical properties of their algorithms (and nevertheless often exhibit good results) or traditionally study the existence of Nash equilibria. The latter approach seems, to the eyes of a young researcher in the field, like a struggle to prove, under severe, unrealistic assumptions, the theoretical existence of solutions that — being infinite and of questionable value — will never be leveraged in practice.
Evolutionary game theory
The inception of evolutionary game theory is not recent, yet its far-reaching applications in the area of AI took long to be acknowledged. Originating in biology, it was introduced in 1973, by John M. Smith and George R. Price, as an alternative to classical game theory. The alterations are so profound that we can talk about a whole new approach.
The subject of reasoning is no longer the player itself, but the population of players. Thus, probabilistic strategies are defined as the percentage of players that make a choice, not the probability of one player choosing an action as in classical game theory. This removes the necessity for rational, omniscient agents, as strategies evolve as patterns of behavior. The evolution process resembles Darwinian theory. Players reproduce following the principles of survival of the fittest and random mutations, and can be elegantly described by a set of differential equations, termed the replicator dynamics.
We can see the three important parts of this system in the illustration below. A population represents the team of agents, and is characterized by a mixture of strategies. The game rules determine the payoffs of the population, which can also be seen as the fitness values of an evolutionary algorithm. Finally, the replicator rules describe how the population will evolve based on the fitness values and the mathematical properties of the evolution process.
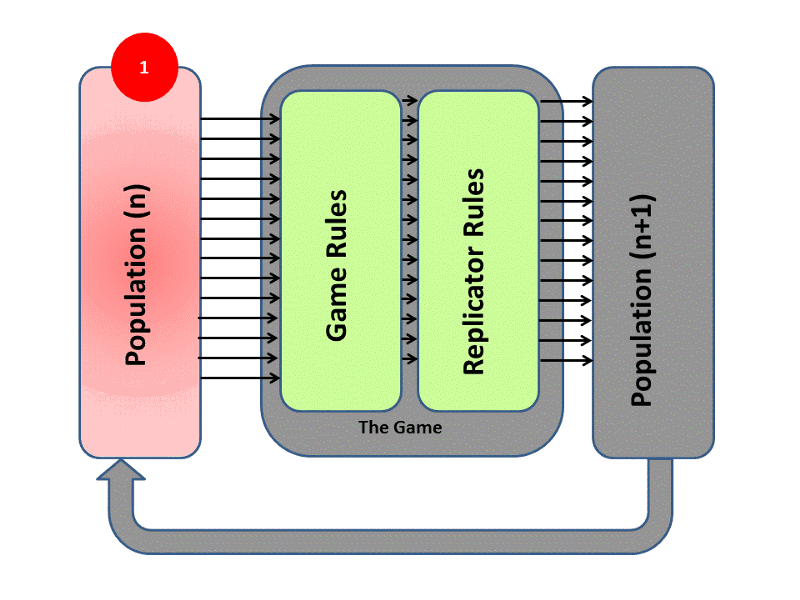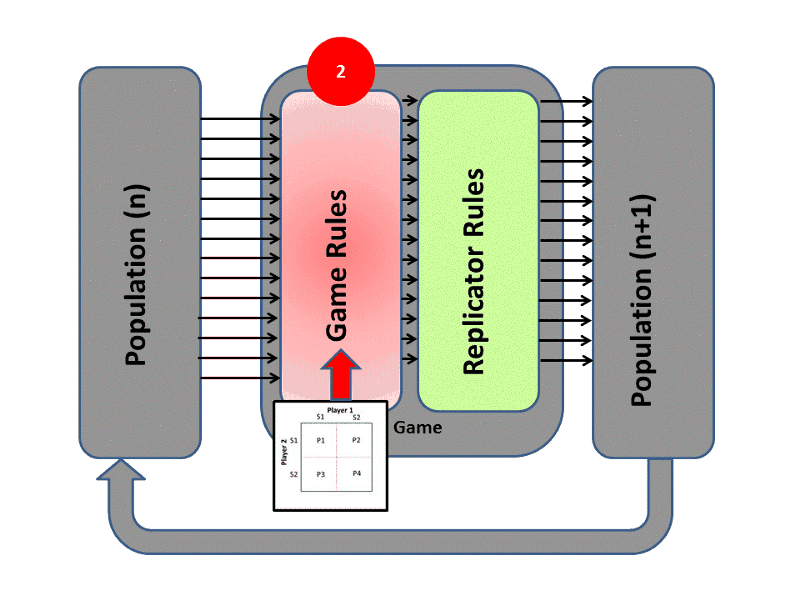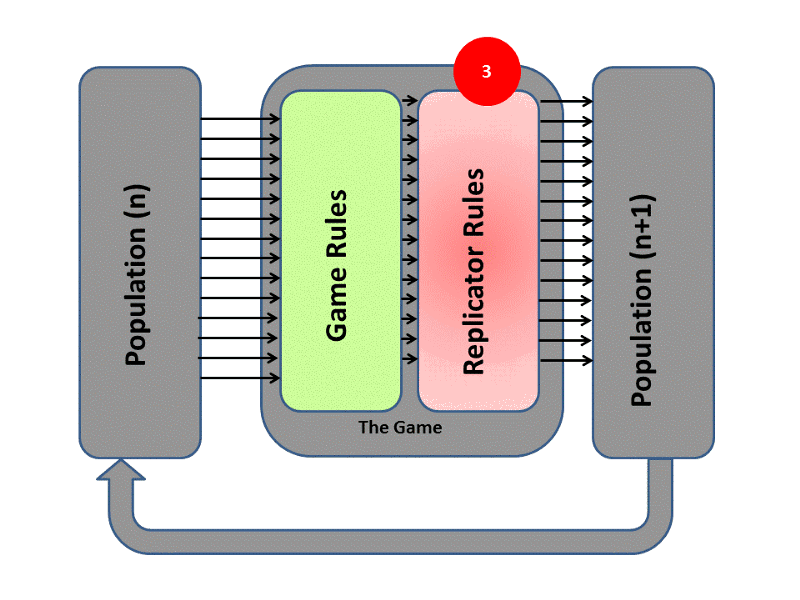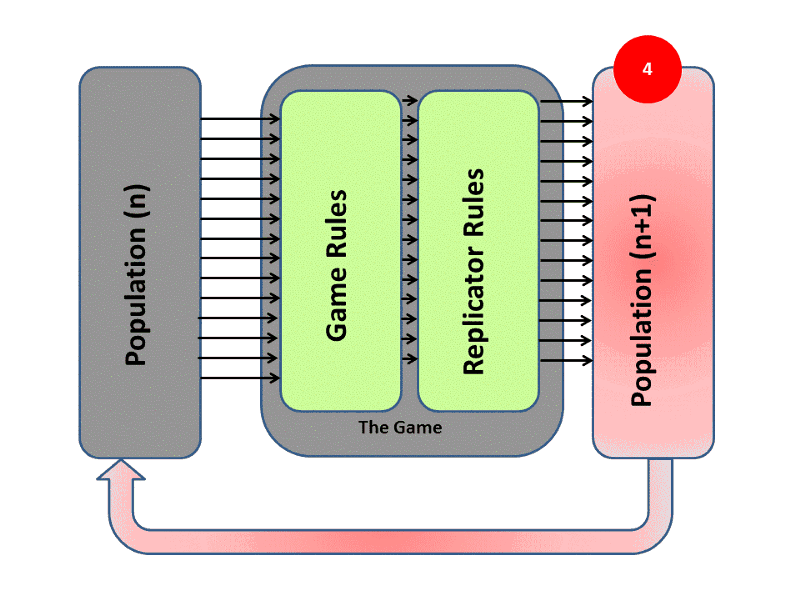
The notion and pursuit of Nash equilibria is replaced by evolutionary stable strategies. A strategy can bear this characterization if it is immune to an invasion by a population of agents that follow another strategy, provided that the invading population is small. Thus, the behavior of the team can be studied under the well-understood area of stability of dynamical systems, such as Lyapunov stability.
The attainment of equilibrium requires a disequilibrium process. What does rational behavior mean in the presence of disequilibrium? Do individuals speculate on the equilibrating process? If they do, can the disequilibrium be regarded as, in some sense, a higher-order equilibrium process?
In the above passage, Arrow seems to be struggling to pinpoint the dynamic properties of a game. Could evolutionary game theory be an answer to his questions?
Quite recently, famous reinforcement learning algorithms, such as Q-learning, were studied under this new approach and significant conclusions were drawn. How this new tool is used ultimately depends on the application.
We can follow the forward approach, to derive the dynamic model of a learning algorithm. Or the inverse, where we start from some desired dynamic properties and engineer a learning algorithm that exhibits them.
We can use the replicator dynamics descriptively, to visualize convergence. Or prescriptively, to tune the algorithm in order to converge to optimal solutions. The latter can immensely reduce the complexity entailed in training deep networks for tough tasks that we face today, by removing the need for blind tuning.
Conclusion
It’s not hard to trace when and why the paths of game theory and AI became convoluted. What’s harder, however, is to overlook the restrictions AI, and in particular multi-agent reinforcement learning, has to face when following classical game theoretic approaches.
Evolutionary game theory sounds promising, offering both theoretical tools and practical advantages, but we won’t really know until we try it. In this case, evolution will not arise naturally, but out of a conscious struggle of the research community for improvement. But isn’t that the essence of evolution?
It takes some effort to deviate from where inertia is pushing you, but reinforcement learning, despite general successes in AI, is in serious need of a lift.
