By Ajay Uppili Arasanipalai
How do companies like Amazon and Netflix know precisely what you want? Whether it’s that new set of speakers that you’ve been eyeballing, or the next Black Mirror episode — their use of predictive algorithms has made the job of selling you stuff ridiculously efficient.
But as much as we’d all like a juicy conspiracy theory, no, they don’t employ psychics.
They use something far more magical — mathematics. Today, we’ll look at an approach called collaborative filtering.
What exactly is collaborative filtering?
As Jeremy Howard mentions in his awesome deep learning course at fast.ai, structured deep learning models don’t get much love these days.
Probably because you wouldn’t get to see stuff like this:
 _Source: [https://cdn.vox-cdn.com/thumbor/NN7jTnph9VCkyyt2nrTFml3XbYw=/0x0:600x338/1200x800/filters:focal(252x121:348x217):no_upscale()/cdn.vox-cdn.com/uploads/chorus_image/image/57380619/ezgif.com_gifmaker__1.0.gif](https://cdn.vox-cdn.com/thumbor/NN7jTnph9VCkyyt2nrTFml3XbYw=/0x0:600x338/1200x800/filters:focal(252x121:348x217):no_upscale()/cdn.vox-cdn.com/uploads/chorus_image/image/57380619/ezgif.com_gifmaker__1.0.gif" rel="noopener" target="blank" title=")
_Source: [https://cdn.vox-cdn.com/thumbor/NN7jTnph9VCkyyt2nrTFml3XbYw=/0x0:600x338/1200x800/filters:focal(252x121:348x217):no_upscale()/cdn.vox-cdn.com/uploads/chorus_image/image/57380619/ezgif.com_gifmaker__1.0.gif](https://cdn.vox-cdn.com/thumbor/NN7jTnph9VCkyyt2nrTFml3XbYw=/0x0:600x338/1200x800/filters:focal(252x121:348x217):no_upscale()/cdn.vox-cdn.com/uploads/chorus_image/image/57380619/ezgif.com_gifmaker__1.0.gif" rel="noopener" target="blank" title=")
But structured algorithms like collaborative filtering are the ones being used most often in the real world. They’re the reason that the stuff that shows up on the bottom of the page on Amazon seems so tempting to buy.
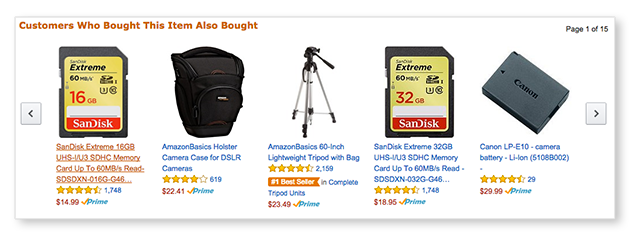 _Source: [https://www.highspot.com/wp-content/uploads/Amazon_Recommended_Edit.png](https://www.highspot.com/wp-content/uploads/Amazon_Recommended_Edit.png" rel="noopener" target="blank" title=")
_Source: [https://www.highspot.com/wp-content/uploads/Amazon_Recommended_Edit.png](https://www.highspot.com/wp-content/uploads/Amazon_Recommended_Edit.png" rel="noopener" target="blank" title=")
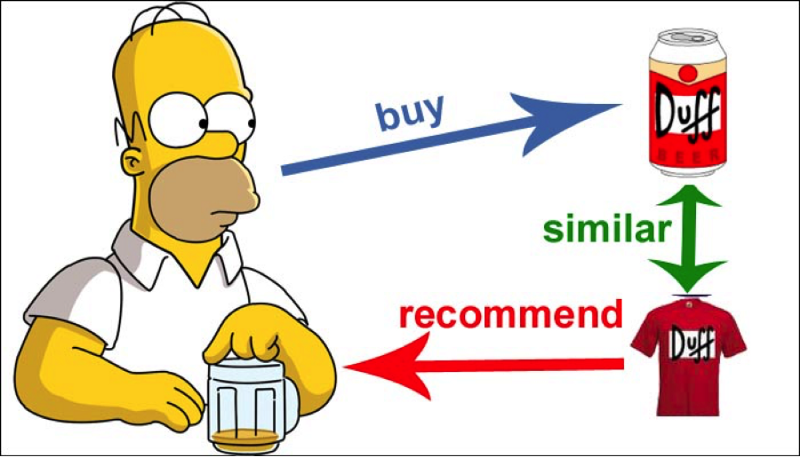
Collaborative filtering works on a fundamental principle: you are likely to like what someone similar to you likes.
The algorithm’s job is to find someone who has buying or watching habits similar to yours, and suggest to you what he/she gave a high rating to.
It can also work the other way around.
The algorithm can recommend a product that is similar to another product that you previously gave a high rating to. All of this similarity checking and comparison is done by some fairly straightforward linear algebra (matrix math).
 _Source: [https://johnolamendy.files.wordpress.com/2015/10/01.png](https://johnolamendy.files.wordpress.com/2015/10/01.png" rel="noopener" target="blank" title=")
_Source: [https://johnolamendy.files.wordpress.com/2015/10/01.png](https://johnolamendy.files.wordpress.com/2015/10/01.png" rel="noopener" target="blank" title=")
Is it really that easy?
Not so fast. Before we start throwing vectors and dot-products around, let’s address a significant problem faced by any recommender system algorithm — the cold start problem.
 _Source: [https://thermex-systems.com/wp-content/uploads/portathaw-cold-start-system-on-heavy-dump-truck.jpg](https://thermex-systems.com/wp-content/uploads/portathaw-cold-start-system-on-heavy-dump-truck.jpg" rel="noopener" target="blank" title=")
_Source: [https://thermex-systems.com/wp-content/uploads/portathaw-cold-start-system-on-heavy-dump-truck.jpg](https://thermex-systems.com/wp-content/uploads/portathaw-cold-start-system-on-heavy-dump-truck.jpg" rel="noopener" target="blank" title=")
You see, collaborative filtering works well when you have two things:
- a lot of data on what each customer likes (based on what they previously rated high)
- a lot of data on what audience each movie or product might cater to (based on the type of people who rated it high).
But how about new users and new products, for which you don’t have much information?
 _Source: [https://1843magazine.static-economist.com/sites/default/files/styles/article-main-image-overlay/public/0312ILIN03-web.jpg](https://1843magazine.static-economist.com/sites/default/files/styles/article-main-image-overlay/public/0312ILIN03-web.jpg" rel="noopener" target="blank" title=")
_Source: [https://1843magazine.static-economist.com/sites/default/files/styles/article-main-image-overlay/public/0312ILIN03-web.jpg](https://1843magazine.static-economist.com/sites/default/files/styles/article-main-image-overlay/public/0312ILIN03-web.jpg" rel="noopener" target="blank" title=")
Collaborative filtering doesn’t work well in these scenarios, so you might have to try something else. Some common solutions involve analyzing metadata or making new users go through a few questions to learn their initial preferences.
 _Source: [http://img.techiesparks.com/2015/07/apple-music-artists.png](http://img.techiesparks.com/2015/07/apple-music-artists.png" rel="noopener" target="blank" title=")
_Source: [http://img.techiesparks.com/2015/07/apple-music-artists.png](http://img.techiesparks.com/2015/07/apple-music-artists.png" rel="noopener" target="blank" title=")
Ok, now onto the cool stuff
Like most machine learning problems, it’s probably a good idea to first take a look at the data. From now on, I’ll be using the example of movies and ratings (mostly inspired by the movielens dataset used in the fast.ai course).
We’re going to visualize it by building a table of users against the score they gave to movies.
Each row represents a user, and each column a movie.
Cross-referencing will tell you what rating a user assigned to a film (on a scale of 1–5, where 0 means ‘didn’t watch’).
We’ll consider our collaborative filtering model a success if it’s able to fill in the zeros. This would mean that it’s able to predict how each user would rate a movie, based on both what the user is like and what the film is like.
Now for the algorithm. We’re going to set up 2 matrices: one for the users and another for the movies. These are called embedding matrices. Let’s call them W_u (for the users) and W_m (for the movies).
Each matrix is going to be filled with e-dimensional vectors (basically arrays of size e). What is e, you ask? It’s a magic number that I’ll address later. For now, just let e be your favorite natural number.
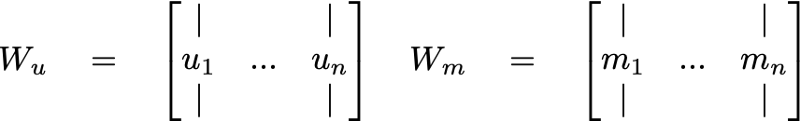
Notice that the table above, if you remove the row and column headings, also looks like a matrix. This is no coincidence. If you’re familiar with matrix multiplication, you’ll know that a 2*3 matrix times a 3*2 matrix gives a 2*2 matrix.
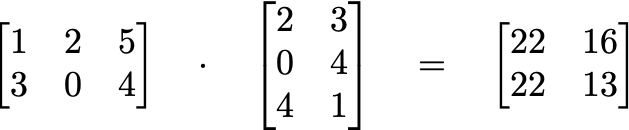
If you want to learn more about matrix multiplication, you should check out this playlist on Khan academy.
Using the same logic, we can multiply our movie and user matrices. The dimensions will work out exactly right to give a matrix that’s the size of the original table dataset (well, technically you have to transpose one of them, but I’m skipping the implementation details).
If we can learn the values of the entries in our movies matrix and user matrix, we could, in theory, get our original table back by multiplying the two.
We have our ground truth: the original table. All we need to do is figure out the numbers (also known as the weights) that somehow multiply together to give us back the original table.
Enter the mystic art of machine learning.
Here’s how we’re going to do it:
- We start off with completely random numbers in the movie matrix and user matrix.
- Then, we multiply the two to get another matrix (which, at this point is also completely random) that looks like our original table.
- By comparing our predicted values with the real values from the table, we define a loss function. This is basically a measure of how far off our predicted rating was from the actual rating.
Note, we also have to skip the zeros, since we don’t want our model predicting a rating of 0 for anyone. That would be pretty useless.
If you want more info on loss functions, I’d recommend Siraj Raval’s video.
After finding the losses, we use backpropagation and gradient descent to optimize the two matrices to get just the right values.
BOOM! We’re done!
Ok, a quick recap:
- We have a table with ratings that each user gave each movie. If a user didn’t watch the movie, the table says ‘0’. We want to predict the zeros.
- To do so, we built two matrices, one for the users, and one for the movies. Each matrix is basically just a stack of e-dimensional vectors.
- To predict ratings, we multiply the matrices together to get another matrix that’s the same shape as the table has our predictions in it. Initially, the table has only gibberish.
- But after using loss functions to find our mistakes, and employing the dynamic duo of backpropagation and gradient descent, we now have a model that can accurately predict what rating a user would give to a movie. Sweet.
Ok… but why does it work?
Now if you’re like me, you get it. But you don’t really get it. How do these random multiplications read minds? Why can’t we just backprop the original table and fill up the zeros? Why go through the elaborate scheme of cooking up two separate matrices and then rebuild the table? Why? Why? Why? Patience, young grasshopper. All is as the force wills it.
Remember how I said that that I was going to address the ‘e’ mystery? Well, now I am.
 _Source: [https://i.imgflip.com/1lai6f.jpg](https://i.imgflip.com/1lai6f.jpg" rel="noopener" target="blank" title=")
_Source: [https://i.imgflip.com/1lai6f.jpg](https://i.imgflip.com/1lai6f.jpg" rel="noopener" target="blank" title=")
Recall that the matrices we constructed were essentially stacks of vectors. One vector per user, and one vector per movie. This was not a meaningless decision.
Each vector is a representation of what kind of person the corresponding user is. It condenses your likes and dislikes, your thoughts and feelings, your hopes and fears, into a numpy.array[] .

To understand this better, let’s zoom into a particular user vector, assuming that e=3:
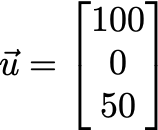
Here, the three components of the vector are[100, 0, 50] . Each component represents some characteristic of the user, which the machine learns from looking at his/her previous rating.
Suppose (and this is not really accurate, it’s just an analogy) that the three components have the following meaning:

Hopefully, you can get a sense of how the vector represents the idea of the user’s preferences.
So in the example above, our good friend u apparently loves action movies, isn’t big on romance movies, and likes comedy movies too, but not as much as action movies.
This is how our machine learning model comprehends human complexity — by embedding it in an e dimensional vector space.
So e is nothing but a little number that we choose (called a hyper-parameter). The bigger it is, the more nuanced information we can capture about our users. But make it too big, and computation will take too long.
But wait. It’s get’s cooler. Take a look at a movie vector:
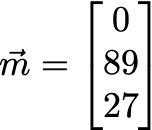
And now, analyze the (human-interpreted) meaning of the components:
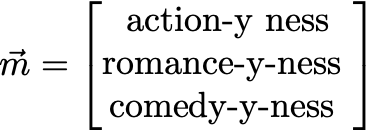
Our blockbuster, m, seems to be a primarily a romance movie, with a fair dose of comedy sprinkled on top. And we know all this without even watching the movie or reading a single review ourselves!
By looking at what types of users gave high and low ratings to movies, the algorithm can now build vectors that represent the essence of what a movie is like.
For the grand finale, consider how we might use this information. We have a user, u and a movie, m. Both are vectors. How do we predict what rating u might give to m? We use the dot product.
The dot product is what you get when you multiply the components of one vector with the components of another, and add up the results. The result is a scalar (a regular, no-strings-attached, good ol’ fashion real number).
So for our case, the dot product of u and m will be:
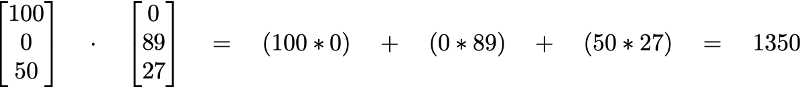
A measly 1350. Well, everything’s relative. But we would have gotten a considerably larger number had we not been multiplying two of the components by 0.
It’s pretty clear that it would be a bad idea to recommend m to u. A terrible idea, in fact.
We Can Make Our Model Even Better
To get the actual rating prediction, we squish the scalar value through a scaled sigmoid function, that bounds the result between 0 and 5.
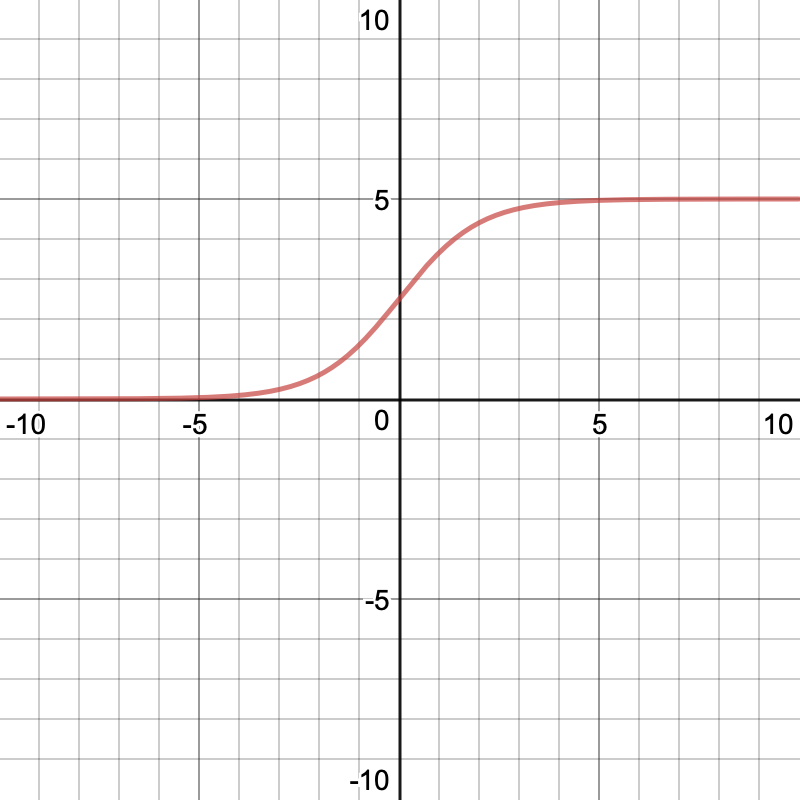 _Source: [https://www.desmos.com/calculator/c4omt4vni3](https://www.desmos.com/calculator/c4omt4vni3" rel="noopener" target="blank" title=")
_Source: [https://www.desmos.com/calculator/c4omt4vni3](https://www.desmos.com/calculator/c4omt4vni3" rel="noopener" target="blank" title=")
If you’re a little concerned about all the hand-wavy tricks we’re doing, rest assured, the computer can figure it all out.
In fact, we’re just making its job easier, by doing things like explicitly telling it that all ratings must be greater bigger than 0 and less than 5.
Here’s another trick — before squishing our scalar value (called an activation) into the sigmoid function, we can add a little number called the bias, b. There will be two biases, one for each user and one for each movie.
Stacking these together, we get a bias vector for the all users (together), and a bias vector for all movies (together). The biases account for some movies being universally loved/hated and some users loving/hating movies in general.
And with that, I present to you the equation that can control your life (or at least, your online shopping/viewing habits):
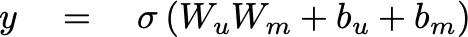
What does any of this mean?
To me, the craziest part about all this is that we are talking about human concepts. Action, romance, comedy, likes, dislikes. All of them are human ideas. And to think that they could all be communicated in a mathematical object is truly fascinating.
Now I know that it’s all just really clearly defined algorithms and human data. But I think there’s still something incredible in the fact that matrix multiplications can teach computers about who we are as individuals.
After all, despite all the things that make us different — what we like, what we look like, who we spend time with, where we are, how we think, how we interact, and how we feel — to the machines that determine what we buy, what we watch, who we talk to, what we do, where we spend our time, and where we don’t, we are all elements of the same linear vector space.
There’s beauty in that.
