By Peter Gleeson
With recent advances in machine learning and AI research making headlines on a regular basis these days, it’s little surprise that data science has become an area of real mainstream interest.
It certainly makes a great career choice for the analytically minded, requiring a blend of solid programming skills and in-depth technical knowledge.
However, behind the show-stealing acts of dueling neural networks and distributed computing are some fundamental statistical practices that every aspiring data scientist should be deeply familiar with.
You can read up on the latest programming frameworks or advances in the scientific literature as required for a specific project. But there are no shortcuts towards acquiring the underlying statistical know-how that makes for an effective data scientist.
Only practice, patience, and maybe just a little learning-the-hard-way, will truly sharpen your “data instincts”.
The principle of parsimony
It’s repeated to the point of cliché in introductory stats courses, but the words of British statistician George Box are perhaps more relevant today than ever before:
“All models are wrong, but some are useful”
What does this statement actually mean?
It means that when seeking to model a real-world system, you necessarily have to simplify and generalise at the expense of explanatory power.
The real world is messy and noisy and difficult to understand to the finest detail. Statistical modelling therefore strives not to achieve perfect predictive power but, rather, maximal predictive power with the minimal necessary model.
This concept can appear counter-intuitive to those new to the world of data. Why not include as many terms in a model as possible? Surely extra terms can only add further explanatory power to the model?
Well, yes… and no. You need only care about terms which bring with them a statistically significant increase in explanatory power.
Consider the different types of model that can be fitted to a given data set.
The most basic is the null model, which has only one parameter — the overall mean of the response variable (plus some randomly distributed error).
This model posits that the response variable doesn’t depend on any of the explanatory variables. Instead, its values are entirely explained by random fluctuation about the overall mean. This obviously limits the model’s explanatory power somewhat.
The polar opposite concept is the saturated model, which has one parameter for every single data point. Here, you have a perfectly fitted model, but one which has no explanatory power should you throw any new data at it.
Including one term per data point also neglects to simplify in any meaningful way. Again — not exactly useful.
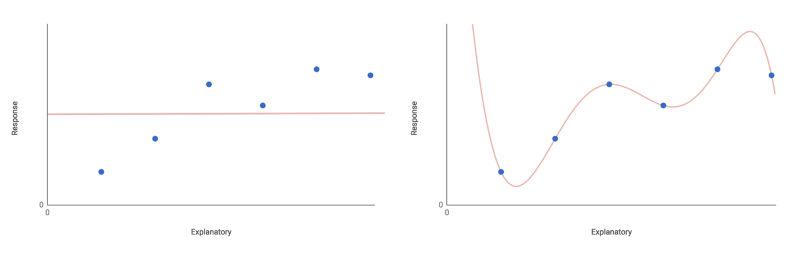
Clearly, those are extreme cases. You should seek a model somewhere in between — one which fits the data well and has good explanatory power. You could try fitting the maximal model. This model includes terms for all factors and interaction terms under consideration.
For example, say you have a response variable y which you want to model as a function of explanatory variables x₁ and x₂, multiplied by coefficients β. The maximal model would look like this:
y = intercept + β₁x₁ + β₂x₂ + β₃(x₁x₂) + error
This maximal model will hopefully fit the data pretty well, and also provide good explanatory power. It includes one term for each explanatory variable, and an interaction term, x₁x₂.
Removing terms from the model will increase the overall residual deviance, or the proportion of observed variation the model’s predictions fail to account for.
However, not all terms are equal. You may be able to remove one (or more) terms, without seeing a statistically significant increase in deviance.
Such terms can be considered insignificant, and removed from the model. You can remove insignificant terms one-by-one (remembering to recalculate the residual deviance at each step). Repeat this until all terms remaining carry statistical significance.
Now you have arrived at the minimal adequate model. The estimates for each term’s coefficient β are significantly different to zero. The step-by-step eliminative approach used to arrive here is known as “stepwise” regression.
The philosophical principle underpinning this drive towards model simplicity is known as the principle of parsimony.
It bears some resemblance to the medieval philosopher William of Ockham’s famous heuristic, Occam’s Razor. This goes along the lines of: “given two or more equally acceptable explanations for a phenomenon, work with the one which introduces the fewest assumptions.”
Or, in other words: can you usefully explain something complex in the simplest way possible? Arguably, this is the defining pursuit of data science — efficiently translating complexity into insight.
Always be sceptical
Hypothesis testing (such as A/B testing) is an important data science concept.
Simply put, hypothesis testing works by reducing a problem to two mutually exclusive hypotheses, and asking under which hypothesis the observed value of a given test statistic is most probable. The test statistic is, of course, calculated from some appropriate set of experimental or observational data.
When it comes to hypothesis testing, you are usually asking whether you accept or reject the null hypothesis.
Often, you hear people describe the null hypothesis as something of a let-down, or even evidence of experimental failure.
Maybe it stems from how hypothesis testing is taught to beginners, but it seems many researchers and data scientists have a subconscious bias against the null hypothesis. They seek to reject it in favour of the supposedly more exciting, more interesting, alternative hypothesis.
This isn’t just an anecdotal problem. Whole research papers have been written on the issue of publication bias within the scientific literature. One can only wonder how this tendency manifests itself within a commercial context.
Yet the fact of the matter is this: for any properly designed experiment or complete-enough data set, accepting the null hypothesis should be just as interesting as accepting the alternative.
Indeed, the null hypothesis is a cornerstone of inferential statistics. It defines what we do as data scientists, which is to turn data into insights. Insights are worth nothing if we’re not hyper-selective about what findings pass muster, and it is for this reason it pays to be ultra-sceptical at all times.
This is especially so, given how easy it is to “accidentally” reject the null hypothesis (at least when applying a frequentist approach naïvely).
Data-dredging (or, ‘p-hacking’) can throw up all manner of meaningless results, which nevertheless appear statistically significant. Where multiple comparisons are unavoidable, there are no excuses for not taking steps to minimise type I errors (false positives, or “seeing effects which are not really there”).
- For a start, when it comes to statistical tests, pick one which is inherently cautious. Check that the test’s assumptions about your data are properly met.
- It is also important to look into correction methods, e.g., Bonferroni correction. However, these methods are sometimes criticised for being overly cautious. They can reduce statistical power by producing too many type II errors (false negatives, or “ignoring effects which do actually exist”).
- Look for “null” explanations for your results. How suitable were your sampling/data collection procedures? Can you rule out any systematic errors? Could there be any effects of survivor bias, autocorrelation, or regression to the mean?
- And finally, how plausible are any potential relationships you’ve found? Never take anything at face value, no matter how low the p-value may be!
Scepticism is healthy, and in general it is good practice to always be mindful of null explanations for your data.
But avoid paranoia! If you’ve designed your experiment well, and analysed your data cautiously, then go ahead and take your findings as real!
Know your methods
Recent technological and theoretical advances have provided data scientists with a range of powerful new tools for solving complex problems that would not have been feasible to tackle even a decade or two ago.
There is a great deal of excitement surrounding these advances in machine learning, and for good reason. However, it is all-too-easy to overlook any limitations there might be in applying them to a given problem.
As an example, neural networks might be brilliant at classifying images and recognising handwriting, but they’re by no means a perfect solution for all problems. For a start, they are very prone to overfitting — that is, getting too familiar with the training data and being unable to generalise to new cases.
Take their opacity as well. The predictive power of neural networks often comes at the cost of transparency. Thanks to the internalisation of feature selection, even if a network makes an accurate prediction, you don’t necessarily understand how it arrived at its answer.
In many business and commercial applications, understanding “how-and-why” is often the most important outcome of an analytical project. Ceding this understanding for the sake of predictive accuracy may or may not be a trade-off worth making.
Likewise, it’s tempting to rely on the accuracy of a sophisticated machine learning algorithm, but they’re absolutely not infallible.
For example, Google’s Cloud Vision API — which is generally very impressive — can be easily tricked by even a small amount of noise in an image. Conversely, another fascinating research paper has shown how Deep Neural Networks can ‘see’ images that are simply not there.

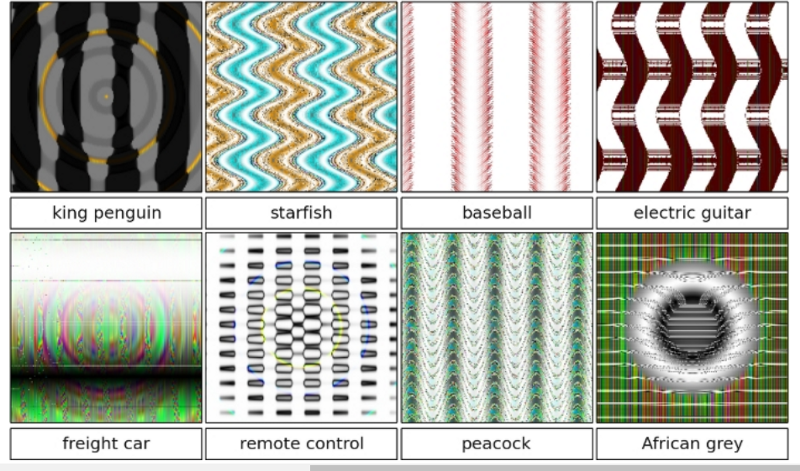
It’s not just cutting-edge Machine Learning methods which need to be used with wariness.
Even with more traditional modelling approaches, care needs to be taken that key assumptions are met. Always eye extrapolation beyond the scope of the training data, if not with suspicion, then at least with caution. With every conclusion you draw, always ask if your methods justify doing so.
This isn’t to say don’t trust any method at all — just to be aware at all times why you’re using one method over another, and what the relative pros/cons might be.
As a general rule, if you can’t come up with at least one drawback of a method you’re considering, research it further before proceeding. Always use the simplest tool that will do the job.
Knowing when is and isn’t appropriate to use a given approach is a key skill in data science. It is a skill which improves with experience and genuine understanding of the methods.
Communication
Communication is the essence of data science. Unlike in academic disciplines, where your target audience will be highly-trained experts in your exact field of study, the audience of a commercial Data Scientist will likely be experts in a wide range of other areas.
Even the best insights in the world are worth nothing if communicated poorly. Many aspiring data scientists come from academic/research backgrounds, and will be used to communicating with technically-specialised audiences.
In a commercial environment, however, it cannot be stressed enough how important it is to explain your findings in a way that a general audience can understand and work with.
For example, your results may be relevant to a range of different departments within an organisation — from marketing, to operations, to product development. Members of each will be experts in their respective fields of work, and will benefit from clear, concise, and relevant summaries of your findings.
As important as the actual results are the known limitations of your findings. Make sure your audience is aware of any key assumptions, missing data, or degrees of uncertainty in your workflow.
The cliche “a picture is worth a thousand words” is especially true in data science. To this end, data visualisation tools are invaluable.
Software such as Tableau, or libraries such as ggplot2 for R and D3.js, are great ways of communicating complex data very effectively. They are worth mastering as much as any technical concept.
Some awareness of graphic design principles will go a long way in making your diagrams look smart and professional.
Be sure to write clearly, too. Evolution has shaped us humans into impressionable creatures full of subconscious biases, and we’re inherently more inclined to trust better presented, well-written information.
Sometimes, the best way to understand a concept is to interact with it yourself — so it may be worth learning a few front-end web skills to produce interactive visualisations that your audience can play around with. There’s no need to reinvent the wheel. Libraries and tools such as D3.js and R’s Shiny make your task much easier.
Thanks for reading! If you have any feedback or comments, please leave a response below — I look forward to reading them!