Sudoku (and its predecessors) has been played for over a hundred years. When it first came out people had to actually solve the puzzles using only their minds. Now we have computers! (Ok, so most people still just use their minds...)
In this article, you will learn how to play and win Sudoku. But more importantly, you will learn how to use machine learning to easily solve every Sudoku puzzle. Who needs thinking when you can let the computer think for you. ?
Peter Norvig developed an elegant program using Python to win sudoku using constraint propagation and search. Norvig's solution is considered a classic and is often referred to when people develop their own code to play Sudoku. After reviewing Sudoku and some strategies, I will break down Norvig's code step-by-step so you can understand how it works.
What is Sudoku?
Sudoku is a number-placement puzzle and there are a few different types. This article is about the most popular type.
The objective is to fill a 9x9 grid with digits (1-9) so that each column, row, and each of the nine 3x3 subgrids (also called boxes) all contain each of the digits from 1 to 9. The puzzles start with some numbers already on the grid and it's up to you to fill in the other numbers.
In the image below from a Sudoku game, the number that should go in the blue highlighted square cannot be in any of the yellow squares corresponding to the column, row, and 3x3 box.

How to solve Sudoku
When solving a Sudoku puzzle, you should be constantly doing two things. The first thing you should do is to eliminate numbers from rows, columns, and boxes (3x3 subgrids). The second thing you should do is to look for a single candidate.
In the example below, the possible numbers for each square are noted in a smaller font. The possible numbers were determined by eliminating all digits that occur in the same column, row, or box. Most people will determine the possible number for one box at a time, instead of for the full grid.
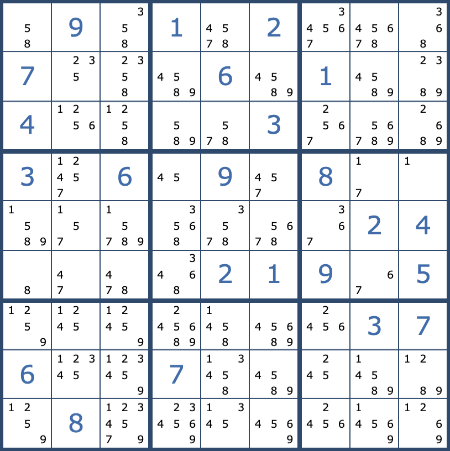
After you eliminate numbers, you can look for single candidates. That means to find a square that can only be one possible number. In the example below, the two yellow highlighted squares must contain 1 and 8 because all the other digits have been eliminated since they already appear in the column, row, or box of the square.
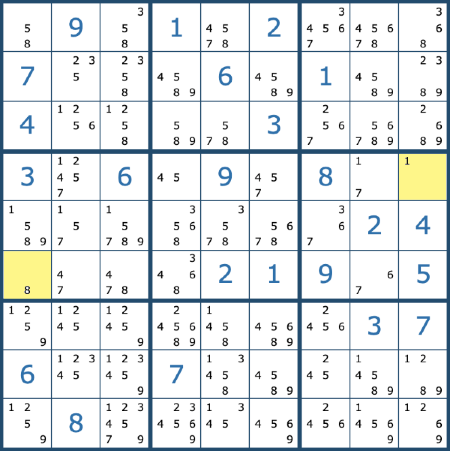
Now that the two squares highlighted in yellow are known, that eliminates more possibilities from other squares. Now you know that the square highlighted in blue must be 7.
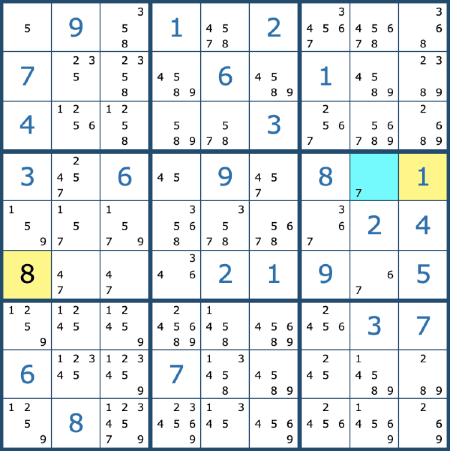
If you keep finding the single candidates and then eliminating options from other squares, you may eventually reach the point where there are no more single candidates.
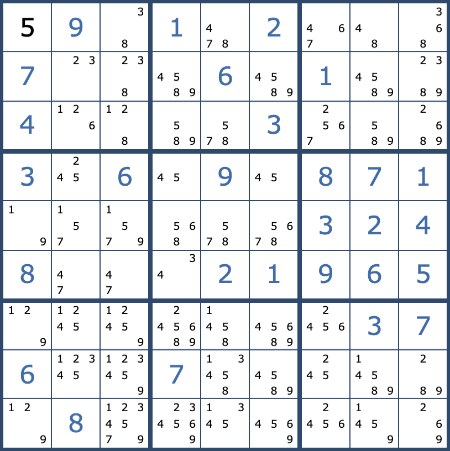
At this point you can look for possible solutions to squares where the number is only in a single square in a box, row, or column. In the example below we can determine that the solution to the square highlighted in blue must be 6 since the number 6 does not occur in any other square in the yellow box.

Sometimes the board will reach a state where it seems that every unsolved square could potentially be multiple values. That means there are multiple paths you could choose and it is not obvious which path will lead to solving the puzzle.
At that point it is necessary to try each option. Choose one and keep solving until it becomes clear that the option you chose cannot be a solution. You will then have to backtrack and try a different option.
This type of searching can be easily done with a computer using a binary search tree. When there is the option of two different numbers to solve a square, it is necessary to brach out into two different possibilities. A binary search tree will allow an algorithm to go down one branch of choices, and then try a different brach of choices.
 Representation of Binary Search Tree
Representation of Binary Search Tree
Now we are going to see Python code that can solve Sudoku puzzles using a similar method to what was just described.
Peter Norvig's program to win Sudoku
Peter Norvig explained his approach to solving Sudoku and the code he used in his article Solving Every Sudoku Puzzle.
Some may find his explanation a little hard to follow, especially beginners. I will break things down so it is easier to understand how Norvig's code works.
In this article, Norvig's Python 2 code has been updated to Python 3. (Python 3 conversion by Naoki Shibuya.) I'll go through the code a few lines at a time but you can see the full code at the end of this article. For some people, it may be helpful to look over the full code before reading on.
First, we'll cover the basic setup and notation. Here's how Norvig describes the basic notation that he uses in his code:
A Sudoku puzzle is a grid of 81 squares; the majority of enthusiasts label the columns 1-9, the rows A-I, and call a collection of nine squares (column, row, or box) a unit and the squares that share a unit the peers.
Here are the names of the squares:
A1 A2 A3| A4 A5 A6| A7 A8 A9
B1 B2 B3| B4 B5 B6| B7 B8 B9
C1 C2 C3| C4 C5 C6| C7 C8 C9
---------+---------+---------
D1 D2 D3| D4 D5 D6| D7 D8 D9
E1 E2 E3| E4 E5 E6| E7 E8 E9
F1 F2 F3| F4 F5 F6| F7 F8 F9
---------+---------+---------
G1 G2 G3| G4 G5 G6| G7 G8 G9
H1 H2 H3| H4 H5 H6| H7 H8 H9
I1 I2 I3| I4 I5 I6| I7 I8 I9
Norvig defines the digits, rows, and columns as strings:
digits = '123456789'
rows = 'ABCDEFGHI'
cols = digits
You will notice that cols is set to equal digits. While they are the same value, the represent different things. The digits variable represents the digits that go in a square to solve the puzzle. The cols variable represents the names of the columns of the grid.
The squares are also defined as strings but the strings are created with a function:
def cross(A, B):
"Cross product of elements in A and elements in B."
return [a+b for a in A for b in B]
squares = cross(rows, cols)
The return part of the cross function ( [a+b for a in A for b in B]) is just a fancy way of writing this code:
squares = []
for a in rows:
for b in cols:
squares.append(a+b)
The squares variable now equals a list of all the square names.
['A1', 'A2', 'A3', 'A4', 'A5', 'A6', 'A7', 'A8', 'A9', 'B1', 'B2', 'B3', 'B4', 'B5', 'B6', 'B7', 'B8', 'B9', 'C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'C9', 'D1', 'D2', 'D3', 'D4', 'D5', 'D6', 'D7', 'D8', 'D9', 'E1', 'E2', 'E3', 'E4', 'E5', 'E6', 'E7', 'E8', 'E9', 'F1', 'F2', 'F3', 'F4', 'F5', 'F6', 'F7', 'F8', 'F9', 'G1', 'G2', 'G3', 'G4', 'G5', 'G6', 'G7', 'G8', 'G9', 'H1', 'H2', 'H3', 'H4', 'H5', 'H6', 'H7', 'H8', 'H9', 'I1', 'I2', 'I3', 'I4', 'I5', 'I6', 'I7', 'I8', 'I9']
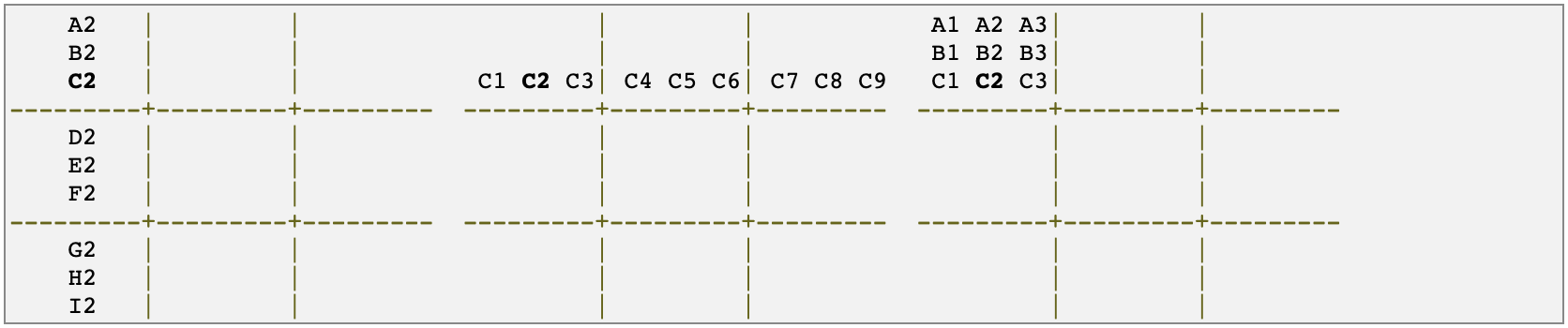
Each square in the grid has 3 units and 20 peers. The units of a square are the row, column, and box that it appears in. The peers of a square are all the other squares in the units. For example, here are the units and peers for the square C2:
All the units for each square are created using the cross function with the following code:
unitlist = ([cross(rows, c) for c in cols] +
[cross(r, cols) for r in rows] +
[cross(rs, cs) for rs in ('ABC','DEF','GHI') for cs in ('123','456','789')])
In Python a dictionary is a collection of key value pairs. The following lines of code creates dictionaries that use the square names as the keys and the three units or 20 peers as the values.
units = dict((s, [u for u in unitlist if s in u])
for s in squares)
peers = dict((s, set(sum(units[s],[]))-set([s]))
for s in squares)
Now, the 3 units of ‘C2’ can be accessed with units['C2'] and will give the following result:
[['A2', 'B2', 'C2', 'D2', 'E2', 'F2', 'G2', 'H2', 'I2'], ['C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'C9'], ['A1', 'A2', 'A3', 'B1', 'B2', 'B3', 'C1', 'C2', 'C3']]
Next we'll need two representations of the full Sudoku playing grid. A textual format named grid will be the initial state of the puzzle.
Another representation of the grid will also be needed to internally describe the current state of a puzzle. It will keep track of all remaining possible values for each square and be named values.
Similar to units and peers, values will be a dictionary with squares as keys. The value of each key will be a string of digits that are the possible digits for the square. If the digit was given in the puzzle or has been figured out, there will only be one digit in the key. For example, if there is a grid where A1 is 6 and A2 is empty, values would look like {'A1': '6', 'A2': '123456789', ...}.
Parse Grid and Grid Values Functions
The parse_grid function (code below) converts the grid to a dictionary of possible values. The grid is the given Sukou puzzle. The grid_values function extracts the important values which are digits, 0, and .. In the values dictionary, the squares are the keys and the given digits in the grid are the values.
For each square with a given value, the assign function is used to assign the value to the square and eliminate the value from the peers. The assign function is covered soon. If anything goes wrong, the function returns False.
Here is the code for the parse_grid and grid_values functions.
def parse_grid(grid):
"""Convert grid to a dict of possible values, {square: digits}, or
return False if a contradiction is detected."""
## To start, every square can be any digit; then assign values from the grid.
values = dict((s, digits) for s in squares)
for s,d in grid_values(grid).items():
if d in digits and not assign(values, s, d):
return False ## (Fail if we can't assign d to square s.)
return values
def grid_values(grid):
"Convert grid into a dict of {square: char} with '0' or '.' for empties."
chars = [c for c in grid if c in digits or c in '0.']
assert len(chars) == 81
return dict(zip(squares, chars))
Constraint Propagation
The initial values for the squares will be either specific digits (1-9) or an empty value. We can apply constraints to each square and eliminate values that are impossible.
Norvig uses two strategies to help determine the correct values for the squares (which correspond to the strategies above):
(1) If a square has only one possible value, then eliminate that value from the square's peers.
(2) If a unit has only one possible place for a value, then put the value there.
An example of the first strategy is that if we know that A1 has a value of 5, then 5 can be removed from all 20 of its peers.
Here is an example of the second strategy: if it can be determined that none of A1 through A8 contains 9 as a possible value, then we can be sure that A9 has a value of 9 since 9 must occur somewhere in the unit.
Every time a square is updated, it will cause possible updates to all its peers. This process will keep continuing and it is called constraint propagation.
Assign Function
The assign(values, s, d) function is called inside the parse_grid function. It returns the updated values. It accepts three arguments: values, s, and d.
Remember, values is a dictionary that associates each square to all possible digit values for that square. s is the square we are assigning a value to and d is the value that needs to be assigned to the square. At the start d comes from the given puzzle we are solving.
It calls the function eliminate(values, s, d) to eliminate every value from s except d.
If there is a contradiction, such as two squares being assigned the same number, the eliminate function will return False.
def assign(values, s, d):
"""Eliminate all the other values (except d) from values[s] and propagate.
Return values, except return False if a contradiction is detected."""
other_values = values[s].replace(d, '')
if all(eliminate(values, s, d2) for d2 in other_values):
return values
else:
return False
Eliminate Function
We saw that the assign function calls the eliminate function. The eliminate function is called like this: eliminate(values, s, d2) for d2 in other_values)
The eliminate function will eliminate values that we know can't be a solution using the two strategies mentioned above. The first strategy is that when there is only one potential value for s, that value is removed from the peers of s. The second strategy is that when there is only one location that a value d can go, that value is removed from all the peers.
Here is the full function:
def eliminate(values, s, d):
"""Eliminate d from values[s]; propagate when values or places <= 2.
Return values, except return False if a contradiction is detected."""
if d not in values[s]:
return values ## Already eliminated
values[s] = values[s].replace(d,'')
## (1) If a square s is reduced to one value d2, then eliminate d2 from the peers.
if len(values[s]) == 0:
return False ## Contradiction: removed last value
elif len(values[s]) == 1:
d2 = values[s]
if not all(eliminate(values, s2, d2) for s2 in peers[s]):
return False
## (2) If a unit u is reduced to only one place for a value d, then put it there.
for u in units[s]:
dplaces = [s for s in u if d in values[s]]
if len(dplaces) == 0:
return False ## Contradiction: no place for this value
elif len(dplaces) == 1:
# d can only be in one place in unit; assign it there
if not assign(values, dplaces[0], d):
return False
return values
Display Function
The display function will display the result after calling parse_grid.
def display(values):
"Display these values as a 2-D grid."
width = 1+max(len(values[s]) for s in squares)
line = '+'.join(['-'*(width*3)]*3)
for r in rows:
print(''.join(values[r+c].center(width)+('|' if c in '36' else '') for c in cols))
if r in 'CF':
print(line)
print()
Here is an example of what the grid will look like after calling the display function after parsing a grid that is a hard puzzle.

You will notice that many of the squares have multiple potential values, while some are completely solved. This grid above is the result of rote application of the two strategies from above. But as you can see, those strategies alone are not enough to completely solve the puzzle.
Search
There are many ways to solve a Sukoku problem but some are much more efficient than others. Norvig suggests a specific type of search algorithm.
There are a few things the search algorithm does. First, it makes sure that no solution or contrition have already been found. Then, it chooses an unfilled square and considers all values that are still possible. Finally, one at a time, it tries to assign the square each value, and searches from the resulting position.
Variable ordering is used to choose which square to start exploring. Here is how Norvig describes it:
we will use a common heuristic called minimum remaining values, which means that we choose the (or one of the) square with the minimum number of possible values. Why? Consider grid2 above. Suppose we chose B3 first. It has 7 possibilities (1256789), so we’d expect to guess wrong with probability 6/7. If instead we chose G2, which only has 2 possibilities (89), we’d expect to be wrong with probability only 1/2. Thus we choose the square with the fewest possibilities and the best chance of guessing right.
The digits are considered in numeric order.
Here is the search function, along with the solve function that parses the initial grid and calls search.
def solve(grid): return search(parse_grid(grid))
def search(values):
"Using depth-first search and propagation, try all possible values."
if values is False:
return False ## Failed earlier
if all(len(values[s]) == 1 for s in squares):
return values ## Solved!
## Chose the unfilled square s with the fewest possibilities
n,s = min((len(values[s]), s) for s in squares if len(values[s]) > 1)
return some(search(assign(values.copy(), s, d))
for d in values[s])
Per the rules of Sudoku, the puzzle is solved when each square has only one value. The search function is called recursively until the puzzle is solved. values is copied to avoid complexity.
Here is the some function used to check if an attempt succeeds to solve the puzzle.
def some(seq):
"Return some element of seq that is true."
for e in seq:
if e: return e
return False
This code will now solve every Sudoku puzzle. You can view the full code below.
Full Sudoku solver code
def cross(A, B):
"Cross product of elements in A and elements in B."
return [a+b for a in A for b in B]
digits = '123456789'
rows = 'ABCDEFGHI'
cols = digits
squares = cross(rows, cols)
unitlist = ([cross(rows, c) for c in cols] +
[cross(r, cols) for r in rows] +
[cross(rs, cs) for rs in ('ABC','DEF','GHI') for cs in ('123','456','789')])
units = dict((s, [u for u in unitlist if s in u])
for s in squares)
peers = dict((s, set(sum(units[s],[]))-set([s]))
for s in squares)
def parse_grid(grid):
"""Convert grid to a dict of possible values, {square: digits}, or
return False if a contradiction is detected."""
## To start, every square can be any digit; then assign values from the grid.
values = dict((s, digits) for s in squares)
for s,d in grid_values(grid).items():
if d in digits and not assign(values, s, d):
return False ## (Fail if we can't assign d to square s.)
return values
def grid_values(grid):
"Convert grid into a dict of {square: char} with '0' or '.' for empties."
chars = [c for c in grid if c in digits or c in '0.']
assert len(chars) == 81
return dict(zip(squares, chars))
def assign(values, s, d):
"""Eliminate all the other values (except d) from values[s] and propagate.
Return values, except return False if a contradiction is detected."""
other_values = values[s].replace(d, '')
if all(eliminate(values, s, d2) for d2 in other_values):
return values
else:
return False
def eliminate(values, s, d):
"""Eliminate d from values[s]; propagate when values or places <= 2.
Return values, except return False if a contradiction is detected."""
if d not in values[s]:
return values ## Already eliminated
values[s] = values[s].replace(d,'')
## (1) If a square s is reduced to one value d2, then eliminate d2 from the peers.
if len(values[s]) == 0:
return False ## Contradiction: removed last value
elif len(values[s]) == 1:
d2 = values[s]
if not all(eliminate(values, s2, d2) for s2 in peers[s]):
return False
## (2) If a unit u is reduced to only one place for a value d, then put it there.
for u in units[s]:
dplaces = [s for s in u if d in values[s]]
if len(dplaces) == 0:
return False ## Contradiction: no place for this value
elif len(dplaces) == 1:
# d can only be in one place in unit; assign it there
if not assign(values, dplaces[0], d):
return False
return values
def solve(grid): return search(parse_grid(grid))
def search(values):
"Using depth-first search and propagation, try all possible values."
if values is False:
return False ## Failed earlier
if all(len(values[s]) == 1 for s in squares):
return values ## Solved!
## Chose the unfilled square s with the fewest possibilities
n,s = min((len(values[s]), s) for s in squares if len(values[s]) > 1)
return some(search(assign(values.copy(), s, d))
for d in values[s])
def some(seq):
"Return some element of seq that is true."
for e in seq:
if e: return e
return False

