By Alexander Arobelidze
A linear equation is an equation that graphs a line. A system of linear equations is when there are two or more linear equations grouped together.
To simplify the illustration, we will consider systems of two equations. As the name suggests, there are two unknown variables. Often they are designated by the letters x and y. If equations describe some process, the letters can be chosen by the roles they play. For example, d can stand for distance, and t for time.
In this article we will learn how to solve systems of linear equations using two fun methods. But before we start, let's see how we end up with a particular system by looking at a real life example.
Deriving a system
A boy gets on his bicycle and starts riding to school. He rides 200 yards every minute.
6 minutes later, his mother realizes her son forgot his lunch. She gets on her own bicycle and starts following the boy. She rides 500 yards every minute (She is an Olympian and a gold medalist).
We want to figure out how long it takes the mother to catch up to the boy, and how far she needs to ride to do so.
Since the boy covers 200 yards every minute, in t minutes he will cover 200 times t yards, or 200t yards.
His mother starts bicycling 6 minutes later, so she rides for (t - 6) minutes. Since she covers 500 yards every minute, in (t - 6) minutes she covers 500 times (t - 6) yards, or 500(t - 6) yards.
By the time she catches up to him, they both have covered the same distance. Let's say for now that distance is d.
For the boy we have d = 200t and for his mother we have d = 500(t - 6). We now have our system of two equations.
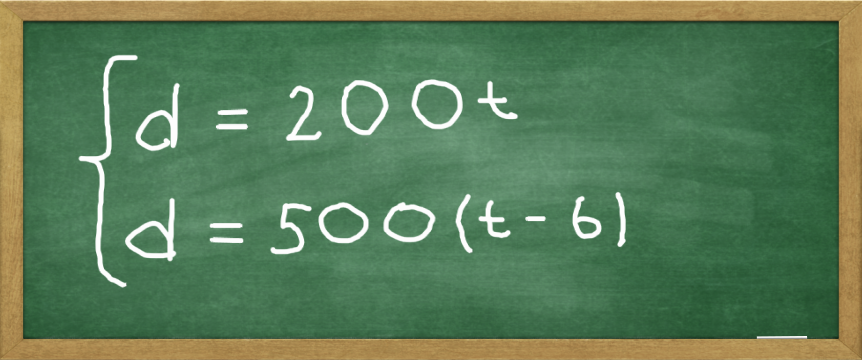 A system of two equations d=200t and d=500(t - 6)
A system of two equations d=200t and d=500(t - 6)
A curly brace is often added to indicate that equations form a system.
Now let's see how we can solve this system.
Solving by substitution
The first method we will consider uses substitution.
We have two unknowns here, d and t. The idea is to get rid of one variable by expressing it using the other variable.
The top equation tells us that d = 200t, so let's plug in 200t for the d in the bottom equation. As a result, we have an equation with just the t variable.
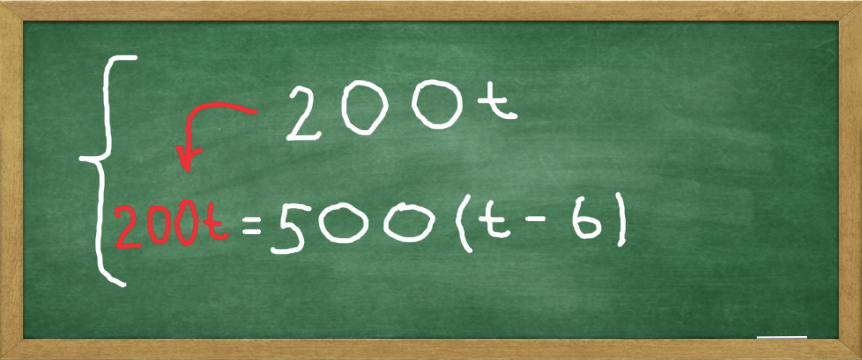 An equation with a single variable 200t = 500(t - 6)
An equation with a single variable 200t = 500(t - 6)
First we expand the right side: 500(t -6) = 500t - 5006 = *500t - 3000.
Then we simplify by moving the unknown members to one side and the known members to the other. The result is: 500t - 200t = 3000.
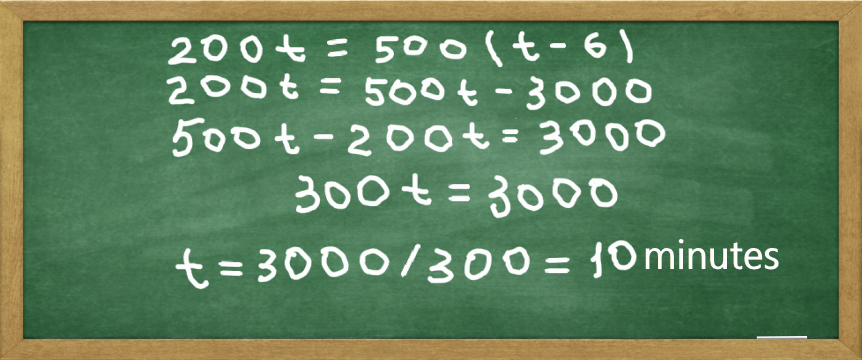 Solving of equation 300t = 3000 results in t = 10
Solving of equation 300t = 3000 results in t = 10
Solving for t gives us t = 10, or since we measure time in minutes, t = 10 minutes. In other words, the mother will catch up to her son in 10 minutes.
The second part of our problem is to find out how far she had to cycle to catch up with him.
To answer that question, we need to find d. Substituting t = 10 in either equation will give us that answer.
To make it easier, let use the top equation, d = 200t = 200 * 10 = 2000. Since we measure distance in yards, d = 2000 yards.
Let's test your understanding so far – try to solve the next system on your own:
y = 2x
y = 3(x - 1)
Choose 1 answer
x = 1 and y = 2
x = 6 and y = 3
x = 1/2 and y = 2/3
Submit
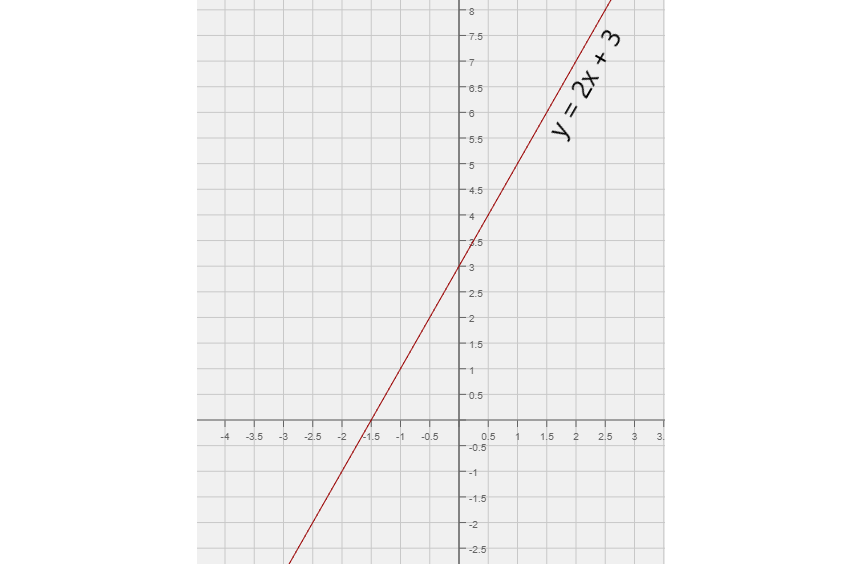 A graph of y = 2x + 3
Next, we can graph a line for y = 9 - x:
A graph of y = 2x + 3
Next, we can graph a line for y = 9 - x: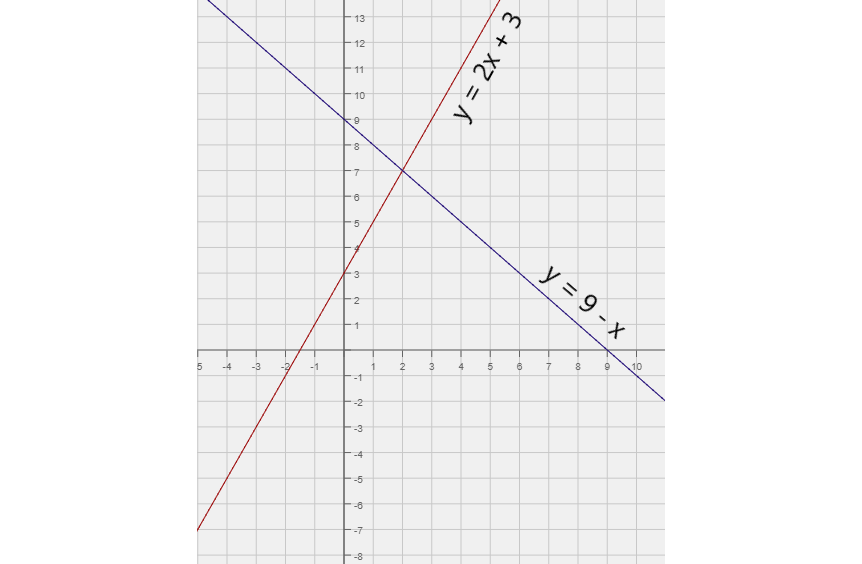 Graphs of y = 2x + 3 and y = 9 - x
These two lines intersect at exactly one point. This point is the only solution to both equations:
Graphs of y = 2x + 3 and y = 9 - x
These two lines intersect at exactly one point. This point is the only solution to both equations:
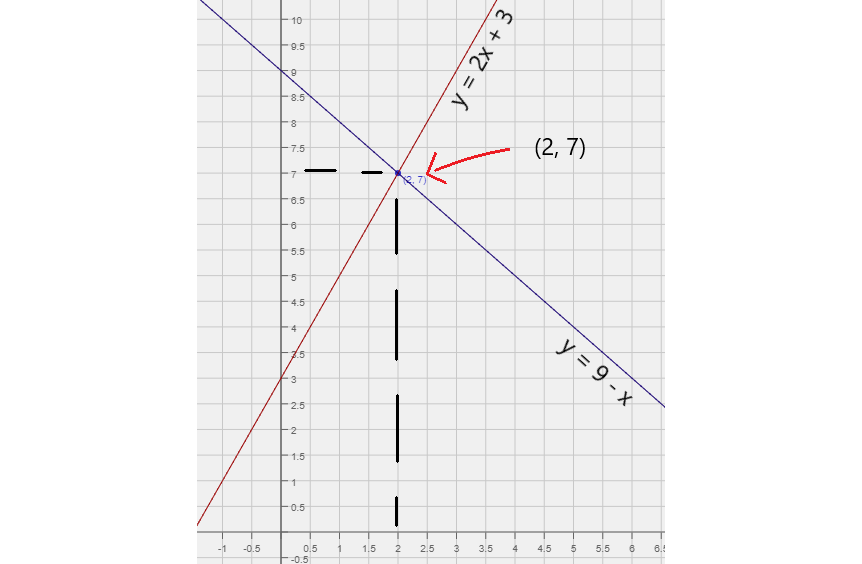 Graphs of y = 2x + 3 and y = 9 - x intersect at (2, 7) point
The ordered pair (2, 7) gives us the coordinates of our point of intersection. This pair is the solution to the system. Substituting x = 2 and y = 7 will let us verify this.
What if the graphs are parallel and do not intersect at all? For example:
Graphs of y = 2x + 3 and y = 9 - x intersect at (2, 7) point
The ordered pair (2, 7) gives us the coordinates of our point of intersection. This pair is the solution to the system. Substituting x = 2 and y = 7 will let us verify this.
What if the graphs are parallel and do not intersect at all? For example:
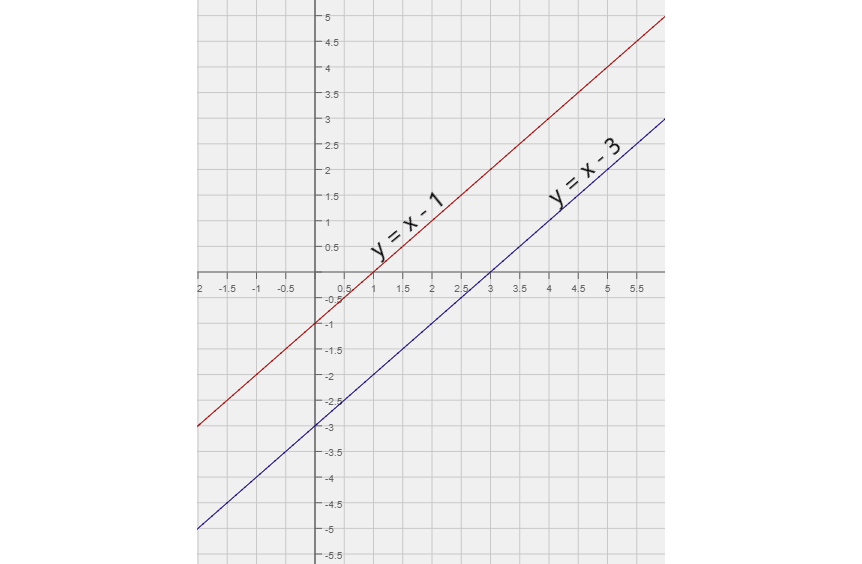 Graphs of y = x - 1 and y = x - 3
When graphs of the equations do not intersect, that means our system has no solution. Trying to solve by substitution will prove that.
The result of x - 1 = x - 3 will be 0 = -2, which is always false.
But what if two graphs are the same and are directly on top of each other?
Graphs of y = x - 1 and y = x - 3
When graphs of the equations do not intersect, that means our system has no solution. Trying to solve by substitution will prove that.
The result of x - 1 = x - 3 will be 0 = -2, which is always false.
But what if two graphs are the same and are directly on top of each other?
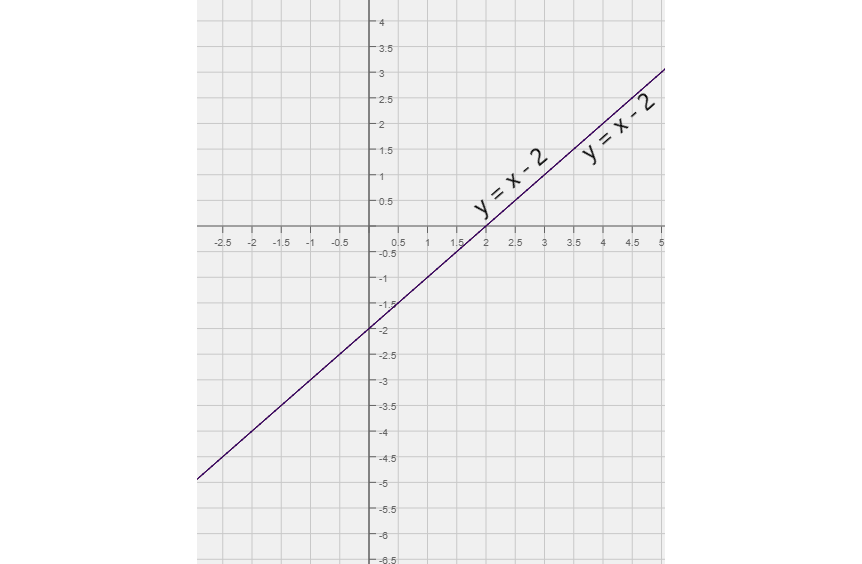 Graphs of y = x - 2 and y = x - 2
In such cases there are an infinite number of points of intersection. That means our system has an infinite number of solutions. Using the substitution method will prove that.
The result of x - 2 = x - 2 is 0 = 0, which is always true.
## More practice
Try using both the substitution and graphing methods to solve the following systems. These methods complement each other and will help you solidify your knowledge.
Graphs of y = x - 2 and y = x - 2
In such cases there are an infinite number of points of intersection. That means our system has an infinite number of solutions. Using the substitution method will prove that.
The result of x - 2 = x - 2 is 0 = 0, which is always true.
## More practice
Try using both the substitution and graphing methods to solve the following systems. These methods complement each other and will help you solidify your knowledge.
y = 2
3y - 2x = 4
Choose 1 answer
x = 1/2 and y = 1
x = 1 and y = 2
x = 0 and y = 2
Submit
x + 5y = 7
3x - 2y = 4
Choose 1 answer
x = 1 and y = 2
x = 1 and y = 1
x = 2 and y = 1
Submit
-6x - 8y = 4
y = -x - 1
Choose 1 answer
Infinite number of solutions
x = 2 and y = -1
x = -1/6 and y = 6
Submit
Now that you know enough about substitution and graphing, get out there and solve more linear equations.
