Hi everyone! In this article we're going to take a look at algorithms, a key topic when it comes to computer science and software development.
Algorithm is a fancy, sometimes intimidating, and often misunderstood word. It sounds like something really hard and complex, but actually it's nothing more than a set of steps that have to be taken in order to achieve a certain goal.
I'd say basic knowledge about algorithms consists of two things mainly:
Asymptotic notation (which we use to compare the performance of one algorithm against another).
A general knowledge of classic algorithms used for very frequent tasks such as searching, sorting, and traversing.
So that's exactly what we're going to see here.😉
Let's go!
Table of Contents
What is an algorithm?
As mentioned before, an algorithm is just a set of steps that need to be taken in order to achieve a certain goal.
I find that when people hear the word algorithm for the first time they picture something like this...

A scene from Matrix or Mr. Robot
But actually this kind of picture would be more accurate...

A book of recipes
An algorithm is just like a recipe, in the sense that it will indicate the necessary steps that need to be followed in order to achieve your goal.
A recipe for making bread could be:
1- Mix flower, salt, water and yeast
2- Let the dough rise
3- Put in the oven for 30'
4- Let chill and enjoy
Side comment: I hope you appreciate the fact that I'm teaching you how to code and cook at the same time, all for free. 😜
An algorithm to identify if a word is a palindrome or not could be:
function isPalindrome(word) {
// Step 1- Put a pointer at each extreme of the word
// Step 2 - Iterate the string "inwards"
// Step 3 - At each iteration, check if the pointers represent equal values
// If this condition isn't accomplished, the word isn't a palindrome
let left = 0
let right = word.length-1
while (left < right) {
if (word[left] !== word[right]) return false
left++
right--
}
return true
}
isPalindrome("neuquen") // true
isPalindrome("Buenos Aires") // false
Same as with a recipe, in this algorithm we have steps with a certain purpose that are executed in a given order in order to achieve the result we want.
Following Wikipedia:
An algorithm is a finite sequence of well-defined instructions, typically used to solve a class of specific problems or to perform a computation.
Algorithmic complexity
Now that we know what an algorithm is, let's learn how to compare different algorithms against each other.
Let's say we're presented this problem:
Write a function that takes two parameters: A non-empty array of distinct integers and an integer representing a target sum. If any two numbers in the array sum up to the target sum, the function should return them in an array. If no two numbers sum up to the target sum, the function should return an empty array.
This could be a valid solution to the problem:
function twoNumberSum(array, targetSum) {
let result = []
// We use a nested loop to test every possible combination of numbers within the array
for (let i = 0; i < array.length; i++) {
for (let j = i+1; j < array.length; j++) {
// If we find the right combination, we push both values into the result array and return it
if (array[i] + array[j] === targetSum) {
result.push(array[i])
result.push(array[j])
return result
}
}
}
// Return the result array
return result
}
console.log(twoNumberSum([9,1,3,4,5], 6)) // [1,5]
console.log(twoNumberSum([1,2,3,4,5], 10)) // []
This could be another valid solution:
function twoNumberSum(array, targetSum) {
// Sort the array and iterate it with one pointer at each extreme
// At each iteration, check if the sum of the two pointers is bigger or smaller than the target
// If it's bigger, move the right pointer to the left
// If it's smaller, move the left pointer to the right
let sortedArray = array.sort((a,b) => a-b)
let leftLimit = 0
let rightLimit = sortedArray.length-1
while (leftLimit < rightLimit) {
const currentSum = sortedArray[leftLimit] + sortedArray[rightLimit]
if (currentSum === targetSum) return [sortedArray[leftLimit], sortedArray[rightLimit]]
else currentSum < targetSum ? leftLimit++ : rightLimit--
}
return []
}
console.log(twoNumberSum([9,1,3,4,5], 6)) // [1,5]
console.log(twoNumberSum([1,2,3,4,5], 10)) // []
And this could be yet another valid solution:
function twoNumberSum(array, targetSum) {
// Iterate over array once, and at each iteration
// check if the number you need to get to ther target exists in the array
// If it exists, return its index and the present number index
let result = []
for (let i = 0; i < array.length; i++) {
let desiredNumber = targetSum - array[i]
if (array.indexOf(desiredNumber) !== -1 && array.indexOf(desiredNumber) !== i) {
result.push(array[i])
result.push(array[array.indexOf(desiredNumber)])
break
}
}
return result
}
console.log(twoNumberSum([9,1,3,4,5], 6)) // [1,5]
console.log(twoNumberSum([1,2,3,4,5], 10)) // []
So how can we compare which solution is better? They all accomplish their goal, right?
But besides effectiveness (whether the goal is achieved or not), we should also evaluate algorithms in terms of efficiency, meaning which solves the problem using the smallest amount of resources in terms of time (processing time) and space (memory usage).
An automatic thought that comes up when first thinking about this is, "Just measure how long it takes the algorithm to run". And that's valid.
But the problem is the same algorithm might take longer or shorter on a different computer given its hardware and configuration. And even in the same computer it might take longer or shorter to run given the background tasks you got running at that given moment.
What we need is an objective and invariable way of measuring an algorithm's performance, and that's exactly what asymptotic notation is for.
Asymptotic notation (also called Big O notation) is a system that allows us to analyze and compare the performance of an algorithm as its input grows.
Big O is a standardized method to analyze and compare the complexity (in terms of runtime and space) of different algorithms. The big O complexity of an algorithm will always be the same no matter what computer you “calculate it” in, because the complexity is calculated on how the number of operations of the algorithm varies when the input varies, and that relationship always stays the same no matter the environment.
There're are a lot of different possible complexities an algorithm can have, but the most common ones are the following:
Constant — O(1): When the number of operations/space required is always the same independently from the input. Take for example a function that takes a number as input and returns that number minus 10. No matter if you give it 100 or 1000000 as input, that function will always perform a single operation (rest 10), so the complexity is constant O(1).
Logarithmic — O(log n): When the number of operations/space required grows at an increasingly slower rate compared to the growth of the input. This type of complexity is often found in algorithms that take a divide and conquer approach or in search algorithms. The classic example is binary search, in which the dataset you have to go through continually halves until you reach the final result.
Linear —O(n): When the number of operations/space required grow at the same rate as the input. Take for example a loop that prints every single value found in an array. The number of operations will grow together with the length of the array, so the complexity is linear O(n).
Quadratic — O(n²): When the number of operations/space required grow at the power of two regarding to the input. Nested loops are the classic example for this one. Imagine we have a loop that iterates through an array of numbers, and within that loop we have another one that iterates the whole array again. For every value in the array we’re iterating over the array twice, so the complexity is quadratic O(n²).

A graphic representation of classic algorithm complexities
Note that the same notation is used when talking about both time and space complexity. Say for example we have a function that always creates an array with a single value no matter the input it receives, then the space complexity will be constant O(1), and so on with the other complexity types.
To better understand all this, let's go back to our problem and analyze our solution examples.
Example 1:
function twoNumberSum(array, targetSum) {
let result = []
// We use a nested loop to test every possible combination of numbers within the array
for (let i = 0; i < array.length; i++) {
for (let j = i+1; j < array.length; j++) {
// If we find the right combination, we push both values into the result array and return it
if (array[i] + array[j] === targetSum) {
result.push(array[i])
result.push(array[j])
return result
}
}
}
// Return the result array
return result
}
console.log(twoNumberSum([9,1,3,4,5], 6)) // [1,5]
console.log(twoNumberSum([1,2,3,4,5], 10)) // []
In this example we're iterating over the parameter array, and for each value within the array, we're iterating the whole array again looking for a number that sums up to the target sum.
Each iteration counts as a task.
If we had 3 numbers in the array, we would iterate 3 times for each number and 9 more times (3 times the three numbers in the array.) 12 tasks total.
If we had 4 numbers in the array, we would iterate 4 times for each number and 16 more times (4 times the four numbers in the array.) 20 tasks total.
If we had 5 numbers in the array, we would iterate 5 times for each number and 25 more times (5 times the five numbers in the array.) 25 tasks total.
You can see how the number of tasks in this algorithm grows exponentially and disproportionally compared to the input. The complexity for this algorithm is quadratic – O(n²).
Whenever we see nested loops, we should think quadratic complexity => BAD => There's probably a better way to solve this.
Example 2:
function twoNumberSum(array, targetSum) {
// Sort the array and iterate it with one pointer at each extreme
// At each iteration, check if the sum of the two pointers is bigger or smaller than the target
// If it's bigger, move the right pointer to the left
// If it's smaller, move the left pointer to the right
let sortedArray = array.sort((a,b) => a-b)
let leftLimit = 0
let rightLimit = sortedArray.length-1
while (leftLimit < rightLimit) {
const currentSum = sortedArray[leftLimit] + sortedArray[rightLimit]
if (currentSum === targetSum) return [sortedArray[leftLimit], sortedArray[rightLimit]]
else currentSum < targetSum ? leftLimit++ : rightLimit--
}
return []
}
console.log(twoNumberSum([9,1,3,4,5], 6)) // [1,5]
console.log(twoNumberSum([1,2,3,4,5], 10)) // []
Here we're sorting the algorithm before we iterate it. And then we only iterate it once, using a pointer at each extreme of the array and iterating "inwards".
This is better than the solution before, since we're only iterating once. But we're still sorting the array (which usually has a logarithmic complexity) and then iterating once (which is linear complexity). The algorithmic complexity of this solution is O(n log(n)).
Example 3:
function twoNumberSum(array, targetSum) {
// Iterate over array once, and at each iteration
// check if the number you need to get to ther target exists in the array
// If it exists, return its index and the present number index
let result = []
for (let i = 0; i < array.length; i++) {
let desiredNumber = targetSum - array[i]
if (array.indexOf(desiredNumber) !== -1 && array.indexOf(desiredNumber) !== i) {
result.push(array[i])
result.push(array[array.indexOf(desiredNumber)])
break
}
}
return result
}
console.log(twoNumberSum([9,1,3,4,5], 6)) // [1,5]
console.log(twoNumberSum([1,2,3,4,5], 10)) // []
In this last example, we're only iterating the array once, without doing anything else before. This is the best solution, since we're performing the smallest number of operations. The complexity in this case is linear – O(n).
This is truly the most important concept behind algorithms. Being able to compare different implementations and understand which is more efficient and why is really an important knowledge to have. So if the concept isn't clear for you yet, I encourage you to read the examples again, look for other resources, or check this awesome freeCodeCamp video-course.
Searching algorithms
Once you have a good understanding about algorithmic complexity, the next good thing to know are popular algorithms used to solve very common programming tasks. So let's start with searching.
When searching for a value in a data structure, there are different approaches we can take. We'll take a look at two of the most used options and compare them.
Linear search
Linear search consists of iterating over the data structure one value at a time and checking if that value is the one we’re looking for. It’s probably the most intuitive kind of search and the best we can do if the data structure we’re using isn’t ordered.
Let’s say we have an array of numbers and for this array we want to write a function that takes a number as the input and returns that number’s index in the array. In case it doesn’t exist in the array, it will return -1. A possible approach could be the following:
const arr = [1,2,3,4,5,6,7,8,9,10]
const search = num => {
for (let i = 0; i < arr.length; i++) {
if (num === arr[i]) return i
}
return -1
}
console.log(search(6)) // 5
console.log(search(11)) // -1
As the array isn’t ordered, we don’t have a way of knowing the approximate position of each value, so the best we can do is check one value at a time. The complexity of this algorithm is linear - O(n) since in the worst case scenario we will have to iterate over the whole array once to get the value we’re looking for.
Linear search is the approach used by many built-in JavaScript methods like indexOf, includes, and findIndex.
Binary search
When we have an ordered data structure, there’s a much more efficient approach we can take, binary search. What we do in binary search is the following:
Select the middle value of our data structure and “ask”, is this the value we’re looking for?
If not, we “ask” whether the value we’re looking for is greater or less than the middle value?
If it’s greater, we “discard” all the values smaller than the mid value. If it’s smaller, we “discard” all the values greater than the mid value.
And then we repeat the same operation until we find the given value or the remaining "piece" of the data structure can't be divided anymore.
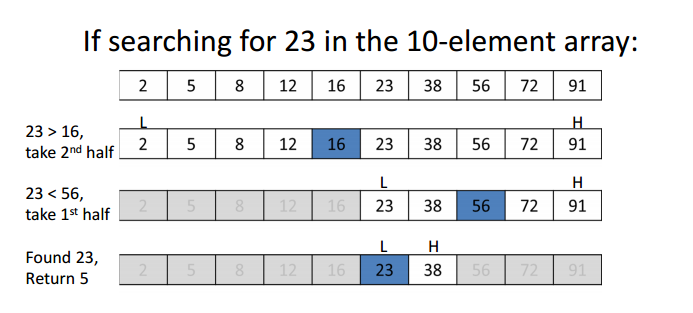
A graphic representation of binary search
What's so cool about binary search is that in each iteration we're discarding roughly half of the data structure. This makes search really quick and efficient. 👌
Let’s say we have the same array (ordered) and we want to write the same function as before, which takes a number as the input and returns that number’s index in the array. In case it doesn’t exist in the array, it will return -1. A binary search approach could be the following:
const arr = [1,2,3,4,5,6,7,8,9,10]
const search = num => {
// We'll use three pointers.
// One at the start of the array, one at the end and another at the middle.
let start = 0
let end = arr.length-1
let middle = Math.floor((start+end)/2)
// While we haven't found the number and the start pointer is equal or smaller to the end pointer
while (arr[middle] !== num && start <= end) {
// If the desired number is smaller than the middle, discard the bigger half of the array
if (num < arr[middle]) end = middle - 1
// If the desired number is bigger than the middle, discard the smaller half of the array
else start = middle + 1
// Recalculate the middle value
middle = Math.floor((start+end)/2)
}
// If we've exited the loop it means we've either found the value or the array can't be devided further
return arr[middle] === num ? middle : -1
}
console.log(search(6)) // 5
console.log(search(11)) // -1
This approach may seem like “more code” at first, but potential iterations are actually a lot less than in linear search, and that’s because in each iteration we’re discarding roughly half of the data structure. The complexity of this algorithm is logarithmic – O(log n).
Sorting algorithms
When sorting data structures, there are many possible approaches we can take. Let’s take a look at some of the most used options and compare them.
Bubble sort
Bubble sort iterates through the data structure and compares one pair of values at a time. If the order of those values is incorrect, it swaps its positions to correct it. The iteration is repeated until the data is ordered. This algorithm makes bigger values “bubble” up to the end of the array.
This algorithm has a quadratic – O(n²) complexity since it will compare each value with the rest of the values one time.
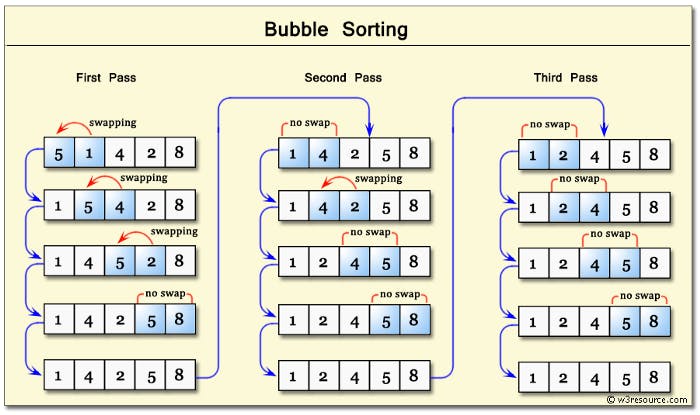
A possible implementation could be the following:
const arr = [3,2,1,4,6,5,7,9,8,10]
const bubbleSort = arr => {
// set a flag variable
let noSwaps
// We will have a nested loop
// with a pointer iterating from right to left
for (let i = arr.length; i > 0; i--) {
noSwaps = true
// and another iterating from right to left
for (let j = 0; j < i-1; j++) {
// We compare the two pointers
if (arr[j] > arr[j+1]) {
let temp = arr[j]
arr[j] = arr[j+1]
arr[j+1] = temp
noSwaps = false
}
}
if (noSwaps) break
}
}
bubbleSort(arr)
console.log(arr) // [1,2,3,4,5,6,7,8,9,10]
Selection sort
Selection sort is similar to bubble sort but instead of placing the bigger values at the end of the data structure, it focuses on placing the smaller values at the beginning. The steps it takes are the following:
Store the first item of the data structure as the minimum value.
Iterate through the data structure comparing each value with the minimum value. If a smaller value is found, it identifies this value as the new minimum value.
If the minimum value isn’t the first value of the data structure, it swaps the positions of the minimum value and the first value.
It repeats this iteration until the data structure is ordered.
This algorithm has a quadratic – O(n²) complexity.
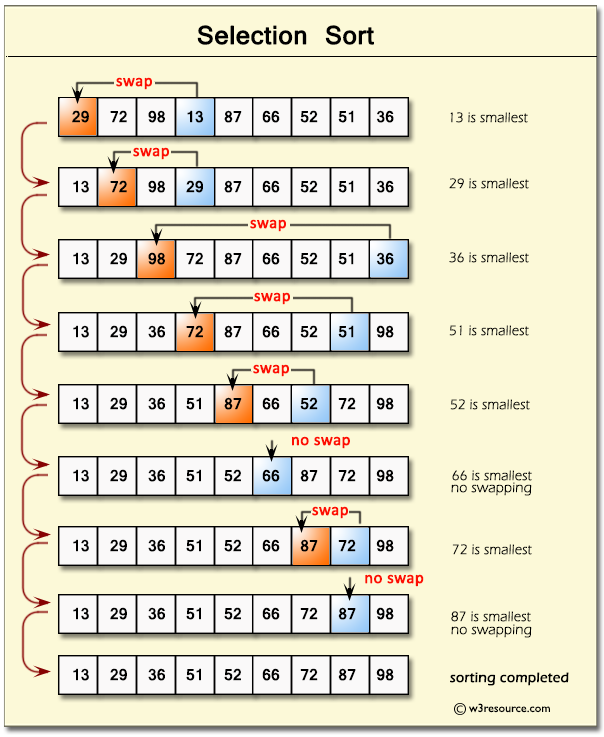
A possible implementation could be the following:
const arr = [3,2,1,4,6,5,7,9,8,10]
const selectionSort = arr => {
for (let i = 0; i < arr.length; i++) {
let lowest = i
for (let j = i+1; j < arr.length; j++) {
if (arr[j] < arr[lowest]) {
lowest = j
}
}
if (i !== lowest) {
let temp = arr[i]
arr[i] = arr[lowest]
arr[lowest] = temp
}
}
}
selectionSort(arr)
console.log(arr) // [1,2,3,4,5,6,7,8,9,10]
Insertion sort
Insertion sort orders the data structure by creating an “ordered half” that is always correctly sorted, and iterates through the data structure picking each value and inserting it in the ordered half exactly in the place it should be.
The steps it takes are the following:
It starts by picking the second element in the data structure.
It compares this element with the one before it and swap its positions if necessary.
It continues to the next element and if it’s not in the right position, it iterates through the “ordered half” to find its correct position and inserts it there.
It repeats the same process until the data structure is sorted.
This algorithm has a quadratic (O(n²)) complexity.
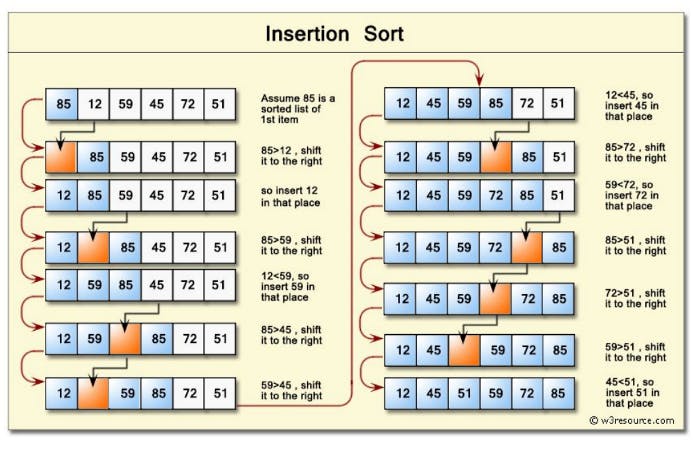
A possible implementation could be the following:
const arr = [3,2,1,4,6,5,7,9,8,10]
const insertionSort = arr => {
let currentVal
for (let i = 0; i < arr.length; i++) {
currentVal = arr[i]
for (var j = i-1; j >= 0 && arr[j] > currentVal; j--) {
arr[j+1] = arr[j]
}
arr[j+1] = currentVal
}
return arr
}
insertionSort(arr)
console.log(arr) // [1,2,3,4,5,6,7,8,9,10]
The problem with bubble sort, selection sort, and insertion sort is that these algorithms don’t scale well.
There’re much better options we can choose when we’re working with big datasets. Some of them are merge sort, quick sort, and radix sort. So let's take a look at those now!
Merge sort
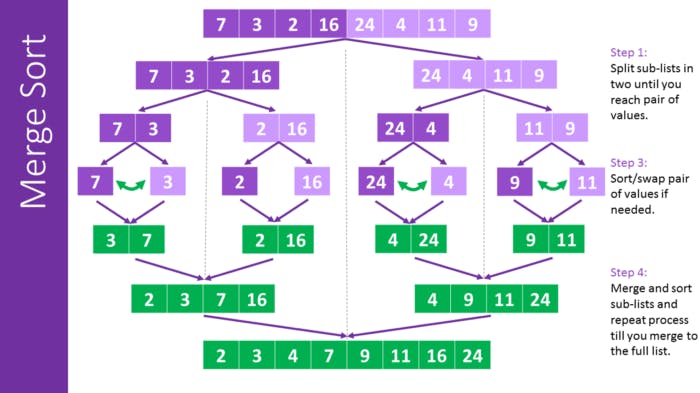
Merge sort is an algorithm that recursively decomposes the data structure into individual values, and then composes it again in a sorted way.
The steps it takes are the following:
Recursively break up the data structure into halves until each “piece” has only one value.
Then, recursively merge the pieces in a sorted way until it gets back to the length of the original data structure.
This algorithm has a O(n log n) complexity, since the decomposition part of it has a complexity of log n and the comparison part of it has a complexity of n.
A possible implementation could be the following:
const arr = [3,2,1,4,6,5,7,9,8,10]
// Merge function
const merge = (arr1, arr2) => {
const results = []
let i = 0
let j = 0
while (i < arr1.length && j < arr2.length) {
if (arr2[j] > arr1[i]) {
results.push(arr1[i])
i++
} else {
results.push(arr2[j])
j++
}
}
while (i < arr1.length) {
results.push(arr1[i])
i++
}
while (j < arr2.length) {
results.push(arr2[j])
j++
}
return results
}
const mergeSort = arr => {
if (arr.length <= 1) return arr
let mid = Math.floor(arr.length/2)
let left = mergeSort(arr.slice(0,mid))
let right = mergeSort(arr.slice(mid))
return merge(left, right)
}
console.log(mergeSort(arr)) // [1,2,3,4,5,6,7,8,9,10]
Quick sort
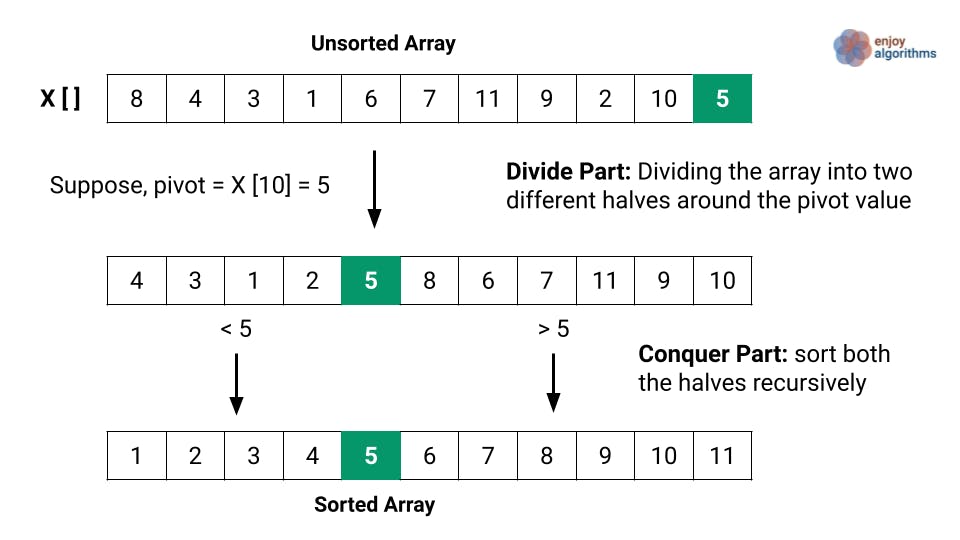
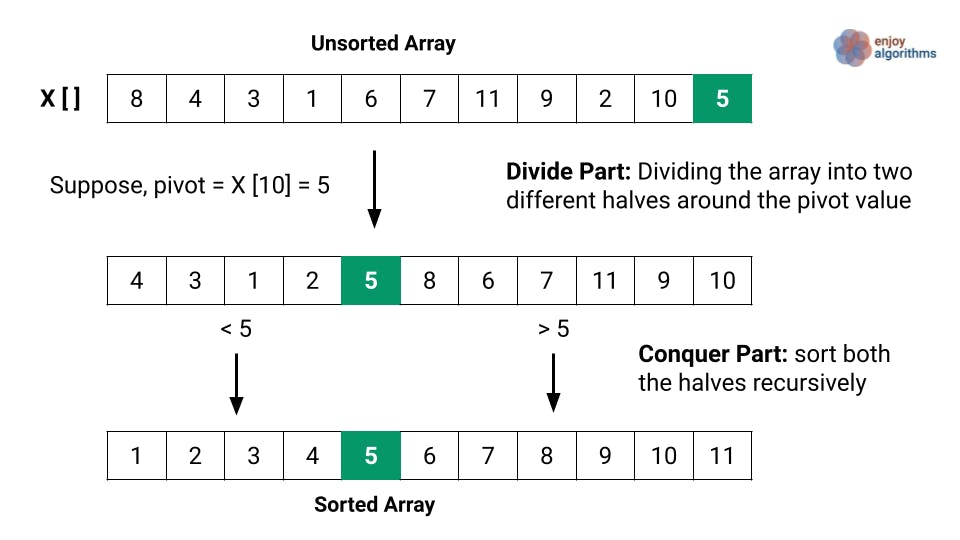
Quick sort works by selecting one element (called “the pivot”) and finding the index where the pivot should end up in the sorted array.
The runtime of quicksort depends in part on how the pivot is selected. Ideally, it should be roughly the median value of the dataset being sorted.
The steps the algorithm takes are the following:
Identify the pivot value and place it in the index it should be.
Recursively execute the same process on each “half” of the data structure.
This algorithm has a O(n log n) complexity.
A possible implementation could be the following:
const arr = [3,2,1,4,6,5,7,9,8,10]
const pivot = (arr, start = 0, end = arr.length - 1) => {
const swap = (arr, idx1, idx2) => [arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]]
let pivot = arr[start]
let swapIdx = start
for (let i = start+1; i <= end; i++) {
if (pivot > arr[i]) {
swapIdx++
swap(arr, swapIdx, i)
}
}
swap(arr, start, swapIdx)
return swapIdx
}
const quickSort = (arr, left = 0, right = arr.length - 1) => {
if (left < right) {
let pivotIndex = pivot(arr, left, right)
quickSort(arr, left, pivotIndex-1)
quickSort(arr, pivotIndex+1, right)
}
return arr
}
console.log(quickSort(arr)) // [1,2,3,4,5,6,7,8,9,10]
Radix sort
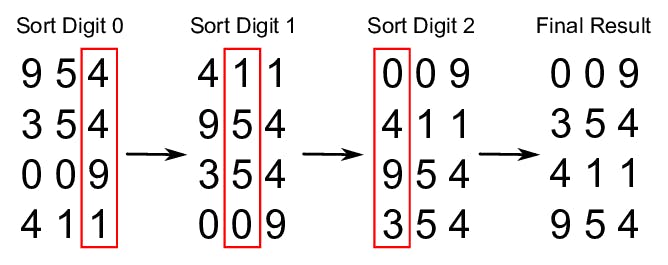
Radix is an algorithm that works in a different way than the ones seen before, in the sense that it doesn’t compare values. Radix is used to sort lists of numbers, and to do so it exploits the fact that the size of a number is defined by the number of digits it has (the more digits, the bigger the number).
What radix does is to sort values by their digits in order. It first sorts all values by the first digit, then again by the second, then by the third… This process is repeated as many times as the number of digits the biggest number in the list has. And by the end of this process, the algorithm returns the fully sorted list.
The steps it takes are the following:
Figure how many digits the largest number has.
Loop through the list up to the largest number of digits. In every iteration:
Create “buckets” for each digit (from 0 to 9) and place each value in its corresponding bucket according to the digit being evaluated.
Replace the existing list with the values sorted in the buckets, starting from 0 and going up to 9.
This algorithm has a O(n*k) complexity, k being the number of digits the largest number has. Given that it doesn’t compare values with each other, this algorithm has a better runtime than the ones seen before, but will only work on lists of numbers.
If we want a data agnostic sorting algorithm, we would probably go with any of the previous ones.
A possible implementation could be the following:
const arr = [3,2,1,4,6,5,7,9,8,10]
const getDigit = (num, i) => Math.floor(Math.abs(num) / Math.pow(10, i)) % 10
const digitCount = num => {
if (num === 0) return 1
return Math.floor(Math.log10(Math.abs(num))) + 1
}
const mostDigits = nums => {
let maxDigits = 0
for (let i = 0; i < nums.length; i++) maxDigits = Math.max(maxDigits, digitCount(nums[i]))
return maxDigits
}
const radixSort = nums => {
let maxDigitCount = mostDigits(nums)
for (let k = 0; k < maxDigitCount; k++) {
let digitBuckets = Array.from({ length: 10 }, () => [])
for (let i = 0; i < nums.length; i++) {
let digit = getDigit(nums[i], k)
digitBuckets[digit].push(nums[i])
}
nums = [].concat(...digitBuckets)
}
return nums
}
console.log(radixSort(arr)) // [1,2,3,4,5,6,7,8,9,10]
Traversing algorithms
The last kind of algorithm we're going to take a look at are traversing algorithms, which are used to iterate through data structures that can be iterated in different ways (mostly trees and graphs).
When iterating a data structure like a tree, we can prioritize iterations in two main ways, either breadth or depth.
If we prioritize depth, we will "descend" through each branch of the tree, going from the head to the leaf of each branch.

Depth first
If we prioritize breadth, we will go through each tree "level" horizontally, iterating through all nodes that are on the same level before "descending" to the next level.

Breadth first
Which one we choose will depend largely on what value we're looking for in our iteration and how our data structure is built.
Breadth first search (BFS)
So let's analyze BFS first. As mentioned, this kind of traversal will iterate through our data structure in a "horizontal way". Following this new example image, the values would be traversed in the following order: [10, 6, 15, 3, 8, 20].

Typically, the steps followed by BFS algorithms are the following:
Create a queue and a variable to store the nodes that have been "visited"
Place the root node inside the queue
Keep looping as long as there's anything in the queue
Dequeue a node from the queue and push the value of the node into the variable that stores the visited nodes
If there's a left property on the dequeued node, add it to the queue
If there's a right property on the dequeued node, add it to the queue
A possible implementation could be the following:
class Node {
constructor(value) {
this.value = value
this.left = null
this.right = null
}
}
class BinarySearchTree {
constructor(){ this.root = null; }
insert(value){
let newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
let current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
BFS(){
let node = this.root,
data = [],
queue = [];
queue.push(node);
while(queue.length){
node = queue.shift();
data.push(node.value);
if(node.left) queue.push(node.left);
if(node.right) queue.push(node.right);
}
return data;
}
}
const tree = new BinarySearchTree()
tree.insert(10)
tree.insert(6)
tree.insert(15)
tree.insert(3)
tree.insert(8)
tree.insert(20)
console.log(tree.BFS()) // [ 10, 6, 15, 3, 8, 20 ]
Depth first search (DFS)
DFS will iterate through our data structure in a "vertical way". Following the same example we used for BFS, the values would be traversed in the following order: [10, 6, 3, 8, 15, 20].
This way of doing DFS is called "pre order". And there're actually three main ways in which DFS can be done, each being different by just changing the order in which nodes are visited.
Pre order: Visit current node, then left node, then right node.
Post order: Explore all children to the left, and all children to the right before visiting the node.
In order: Explore all children to the left, visit the current node, and explore all children to the right.
If this sounds confusing, don't worry. It's not that complex and it will become clearer in short with a few examples.
Pre order DFS
In a pre order DFS algorithm we do the following:
Create a variable to store the values of the visited nodes
Store the root of the tree in a variable
Write a helper function that accepts a node as a parameter
Push the value of the node to the variable that stores values
If the node has a left property, call helper function with left node as parameter
If the node has a right property, call helper function with left node as parameter
A possible implementation could be the following:
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
var newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
var current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
DFSPreOrder(){
var data = [];
function traverse(node){
data.push(node.value);
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
}
traverse(this.root);
return data;
}
}
var tree = new BinarySearchTree()
tree.insert(10)
tree.insert(6)
tree.insert(15)
tree.insert(3)
tree.insert(8)
tree.insert(20)
console.log(tree.DFSPreOrder()) // [ 10, 6, 3, 8, 15, 20 ]
Post order DFS
In post order DFS algorithm we do the following:
Create a variable to store the values of the visited nodes
Store the root of the tree in a variable
Write a helper function that accepts a node as parameter
If the node has a left property, call helper function with left node as parameter
If the node has a right property, call helper function with left node as parameter
Call the helper function with the current node as parameter
A possible implementation could be the following:
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
var newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
var current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
DFSPostOrder(){
var data = [];
function traverse(node){
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
data.push(node.value);
}
traverse(this.root);
return data;
}
}
var tree = new BinarySearchTree()
tree.insert(10)
tree.insert(6)
tree.insert(15)
tree.insert(3)
tree.insert(8)
tree.insert(20)
console.log(tree.DFSPostOrder()) // [ 3, 8, 6, 20, 15, 10 ]
In order DFS
In in order DFS algorithm we do the following:
Create a variable to store the values of the visited nodes
Store the root of the tree in a variable
Write a helper function that accepts a node as parameter
If the node has a left property, call helper function with left node as parameter
Push the value of the node to the variable that stores values
If the node has a right property, call helper function with left node as parameter
Call the helper function with the current node as parameter
A possible implementation could be the following:
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
var newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
var current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
DFSInOrder(){
var data = [];
function traverse(node){
if(node.left) traverse(node.left);
data.push(node.value);
if(node.right) traverse(node.right);
}
traverse(this.root);
return data;
}
}
var tree = new BinarySearchTree()
tree.insert(10)
tree.insert(6)
tree.insert(15)
tree.insert(3)
tree.insert(8)
tree.insert(20)
console.log(tree.DFSInOrder()) // [ 3, 6, 8, 10, 15, 20 ]
As you probably noticed, pre order, post order, and in order implementations are all very similar and we just change the order of how nodes are visited. The traversal result we get to is quite different with each implementation and sometimes one might come in handy more than others.
Regarding when to use BFS or DFS, as I said it depends on how our data structure is organized.
Generally speaking, if we have a very wide tree or graph (meaning there are lots of sibling nodes that stand on the same level), we should prioritize DFS. And if we're dealing with a very large tree or graph that has very long branches, we should prioritize BFS.
The time complexity of both algorithms is the same, as we're always visiting each node just once. But space complexity can be different depending on how many nodes have to be stored in memory for each implementation. So the fewer nodes we have to keep track of, the better.
Wrap up
As always, I hope you enjoyed the article and learned something new. If you want, you can also follow me on LinkedIn or Twitter.
See you later!


