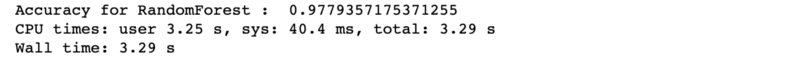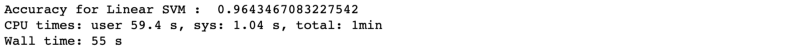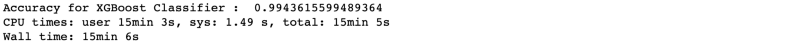By Avishek Nag (Machine Learning expert)
A comparison of different classifiers’ accuracy & performance for high-dimensional data

In Machine learning, classification problems with high-dimensional data are really challenging. Sometimes, very simple problems become extremely complex due this ‘curse of dimensionality’ problem.
In this article, we will see how accuracy and performance vary across different classifiers. We will also see how, when we don’t have the freedom to choose a classifier independently, we can do feature engineering to make a poor classifier perform well.
Understanding the ‘datasource’ & problem formulation
For this article, we will use the “EEG Brainwave Dataset” from Kaggle. This dataset contains electronic brainwave signals from an EEG headset and is in temporal format. At the time of writing this article, nobody has created any ‘Kernel’ on this dataset — that is, as of now, no solution has been given in Kaggle.
So, to start with, let’s first read the data to see what’s there.
There are 2549 columns in the dataset and ‘label’ is the target column for our classification problem. All other columns like ‘mean_d_1_a’, ‘mean_d2_a’ etc are describing features of brainwave signal readings. Columns starting with the ‘fft’ prefix are most probably ‘Fast Fourier transforms’ of original signals. Our target column ‘label’ describes the degree of emotional sentiment.
As per Kaggle, here is the challenge: “Can we predict emotional sentiment from brainwave readings?”
Let’s first understand class distributions from column ‘label’:

So, there are three classes, ‘POSITIVE’, ‘NEGATIVE’ & ‘NEUTRAL’, for emotional sentiment. From the bar chart, it is clear that class distribution is not skewed and it is a ‘multi-class classification’ problem with target variable ‘label’. We will try with different classifiers and see the accuracy levels.
Before applying any classifier, the column ‘label’ should be separated out from other feature columns (‘mean_d_1_a’, ‘mean_d2_a’ etc are features).
label_df = brainwave_df['label']brainwave_df.drop('label', axis = 1, inplace=True)brainwave_df.head()
As it is a ‘classification’ problem, we will follow the below conventions for each ‘classifier’ to be tried:
- We will use a ‘cross validation’ (in our case will use 10 fold cross validation) approach over the dataset and take average accuracy. This will give us a holistic view of the classifier’s accuracy.
- We will use a ‘Pipeline’ based approach to combine all pre-processing and main classifier computation. A ML ‘Pipeline’ wraps all processing stages in a single unit and act as a ‘classifier’ itself. By this, all stages become re-usable and can be put in forming other ‘pipelines’ also.
- We will track total time in building & testing for each approach. We will call this ‘time taken’.
For the above, we will primarily use the scikit-learn package from Python. As the number of features here is quite high, will start with a classifier which works well on high-dimensional data.
RandomForest Classifier
‘RandomForest’ is a tree & bagging approach-based ensemble classifier. It will automatically reduce the number of features by its probabilistic entropy calculation approach. Let’s see that:
Accuracy is very good at 97.7% and ‘total time taken’ is quite short (3.29 seconds only).
For this classifier, no pre-processing stages like scaling or noise removal are required, as it is completely probability-based and not at all affected by scale factors.
Logistic Regression Classifier
‘Logistic Regression’ is a linear classifier and works in same way as linear regression.
We can see accuracy (93.19%) is lower than ‘RandomForest’ and ‘time taken’ is higher (2 min 7s).
‘Logistic Regression’ is heavily affected by different value ranges across dependent variables, thus forces ‘feature scaling’. That’s why ‘StandardScaler’ from scikit-learn has been added as a preprocessing stage. It automatically scales features according to a Gaussian Distribution with zero mean & unit variance, and thus values for all variables range from -1 to +1.
The reason for high time taken is high-dimensionality and scaling time required. There are 2549 variables in the dataset and the coefficient of each one should be optimised as per the Logistic Regression process. Also, there is a question of multi-co-linearity. This means linearly co-related variables should be grouped together instead of considering them separately.
The presence of multi-col-linearity affects accuracy. So now the question becomes, “Can we reduce the number of variables, reduce multi-co-linearity, & improve ‘time taken?”
Principal Component Analysis (PCA)
PCA can transform original low level variables to a higher dimensional space and thus reduce the number of required variables. All co-linear variables get clubbed together. Let’s do a PCA of the data and see what are the main PC’s:
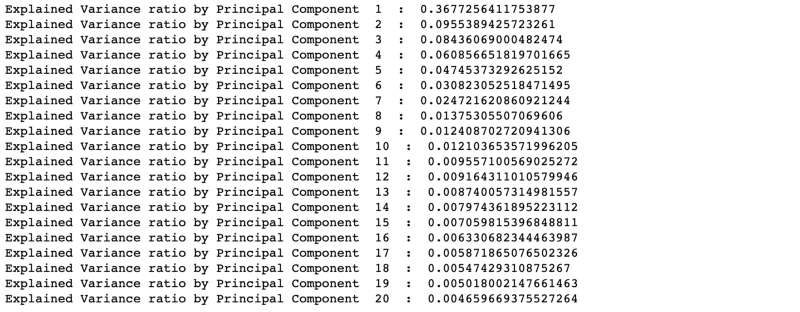
We mapped 2549 variables to 20 Principal Components. From the above result, it is clear that first 10 PCs are a matter of importance. The total percentage of the explained variance ratio by the first 10 PCs is around 0.737 (0.36 + 0.095 + ..+ 0.012). Or it can be said that the first 10 PCs explain 73.7% variance of the entire dataset.
So, with this we are able to reduce 2549 variables to 10 variables. That’s a dramatic change, isn’t it? In theory, Principal Components are virtual variables generated from mathematical mapping. From a business angle, it is not possible to tell which physical aspect of the data is covered by them. That means, physically, that Principal Components don’t exist. But, we can easily use these PCs as quantitative input variables to any ML algorithm and get very good results.
For visualisation, let’s take the first two PCs and see how can we distinguish different classes of the data using a ‘scatterplot’.
plt.figure(figsize=(25,8))sns.scatterplot(x=pca_vectors[:, 0], y=pca_vectors[:, 1], hue=label_df)plt.title('Principal Components vs Class distribution', fontsize=16)plt.ylabel('Principal Component 2', fontsize=16)plt.xlabel('Principal Component 1', fontsize=16)plt.xticks(rotation='vertical');
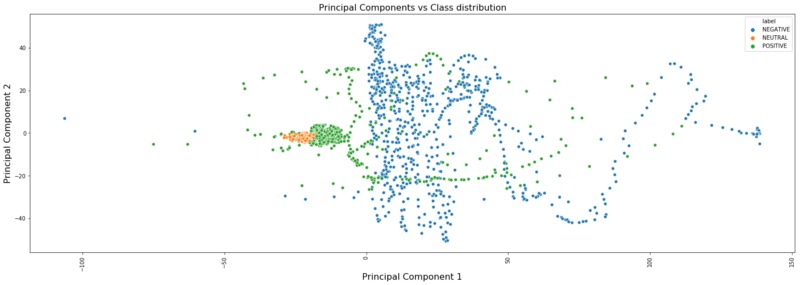
In the above plot, three classes are shown in different colours. So, if we use the same ‘Logistic Regression’ classifier with these two PCs, then from the above plot we can probably say that the first classifier will separate out ‘NEUTRAL’ cases from other two cases and the second classifier will separate out ‘POSITIVE’ & ‘NEGATIVE’ cases (as there will be two internal logistic classifiers for 3-class problem). Let’s try and see the accuracy.
Time taken (3.34 s) was reduced but accuracy (77%) decreased.
Now, let’s take all 10 PCs and run:
We see an improvement in accuracy (86%) compared to 2 PC cases with a marginal increase in ‘time taken’.
So, in both cases we saw low accuracy compared to normal logistic regression, but a significant improvement in ‘time taken’.
Accuracy can be further tested with a different ‘solver’ & ‘max_iter’ parameter. We used ‘saga’ as ‘solver’ with L1 penalty and 200 as ‘max_iter’. These values can be changed to get a variable effect on accuracy.
Though ‘Logistic Regression’ is giving low accuracy, there are situations where it may be needed specially with PCA. In datasets with a very large dimensional space, PCA becomes the obvious choice for ‘linear classifiers’.
In some cases, where a benchmark for ML applications is already defined and only limited choices of some ‘linear classifiers’ are available, this analysis would be helpful. It is very common to see such situations in large organisations where standards are already defined and it is not possible to go beyond them.
Artificial Neural Network Classifier (ANN)
An ANN classifier is non-linear with automatic feature engineering and dimensional reduction techniques. ‘MLPClassifier’ in scikit-learn works as an ANN. But here also, basic scaling is required for the data. Let’s see how it works:
Accuracy (97.5%) is very good, though running time is high (5 min).
The reason for high ‘time taken’ is the rigorous training time required for neural networks, and that too with a high number of dimensions.
It is a general convention to start with a hidden layer size of 50% of the total data size and subsequent layers will be 50% of the previous one. In our case these are (1275 = 2549 / 2, 637 = 1275 / 2). The number of hidden layers can be taken as hyper-parameter and can be tuned for better accuracy. In our case it is 2.
Linear Support Vector Machines Classifier (SVM)
We will now apply ‘Linear SVM’ on the data and see how accuracy is coming along. Here also scaling is required as a preprocessing stage.
Accuracy is coming in at 96.4% which is little less than ‘RandomForest’ or ‘ANN’. ‘time taken’ is 55 s which is in far better than ‘ANN’.
Extreme Gradient Boosting Classifier (XGBoost)
XGBoost is a boosted tree based ensemble classifier. Like ‘RandomForest’, it will also automatically reduce the feature set. For this we have to use a separate ‘xgboost’ library which does not come with scikit-learn. Let’s see how it works:
Accuracy (99.4%) is exceptionally good, but ‘time taken’(15 min) is quite high. Nowadays, for complicated problems, XGBoost is becoming a default choice for Data Scientists for its accurate results. It has high running time due to its internal ensemble model structure. However, XGBoost performs well in GPU machines.
Conclusion
From all of the classifiers, it is clear that for accuracy ‘XGBoost’ is the winner. But if we take ‘time taken’ along with ‘accuracy’, then ‘RandomForest’ is a perfect choice. But we also saw how to use a simple linear classifier like ‘logistic regression’ with proper feature engineering to give better accuracy. Other classifiers don’t need that much feature engineering effort.
It depends on the requirements, use case, and data engineering environment available to choose a perfect ‘classifier’.
The entire project on Jupyter NoteBook can be found here.
References:
[1] XGBoost Documentation — https://xgboost.readthedocs.io/en/latest/
[2] RandomForest workings — http://dataaspirant.com/2017/05/22/random-forest-algorithm-machine-learing/
[3] Principal Component Analysis — https://towardsdatascience.com/a-one-stop-shop-for-principal-component-analysis-5582fb7e0a9c
[4] Logistic Regression — http://ufldl.stanford.edu/tutorial/supervised/LogisticRegression/
[5] Support Vector Machines — https://towardsdatascience.com/support-vector-machine-introduction-to-machine-learning-algorithms-934a444fca47