What is a Red-Black Tree?
Red-Black Tree is a type of self-balancing Binary Search Tree (BST). In a Red-Black Tree, every node follows these rules:
- Every node has two children, colored either red or black.
- Every tree leaf node is always black.
- Every red node has both of its children colored black.
- There are no two adjacent red nodes (A red node cannot have a red parent or red child).
- Every path from root to a tree leaf node has the same number of black nodes (called "black height").
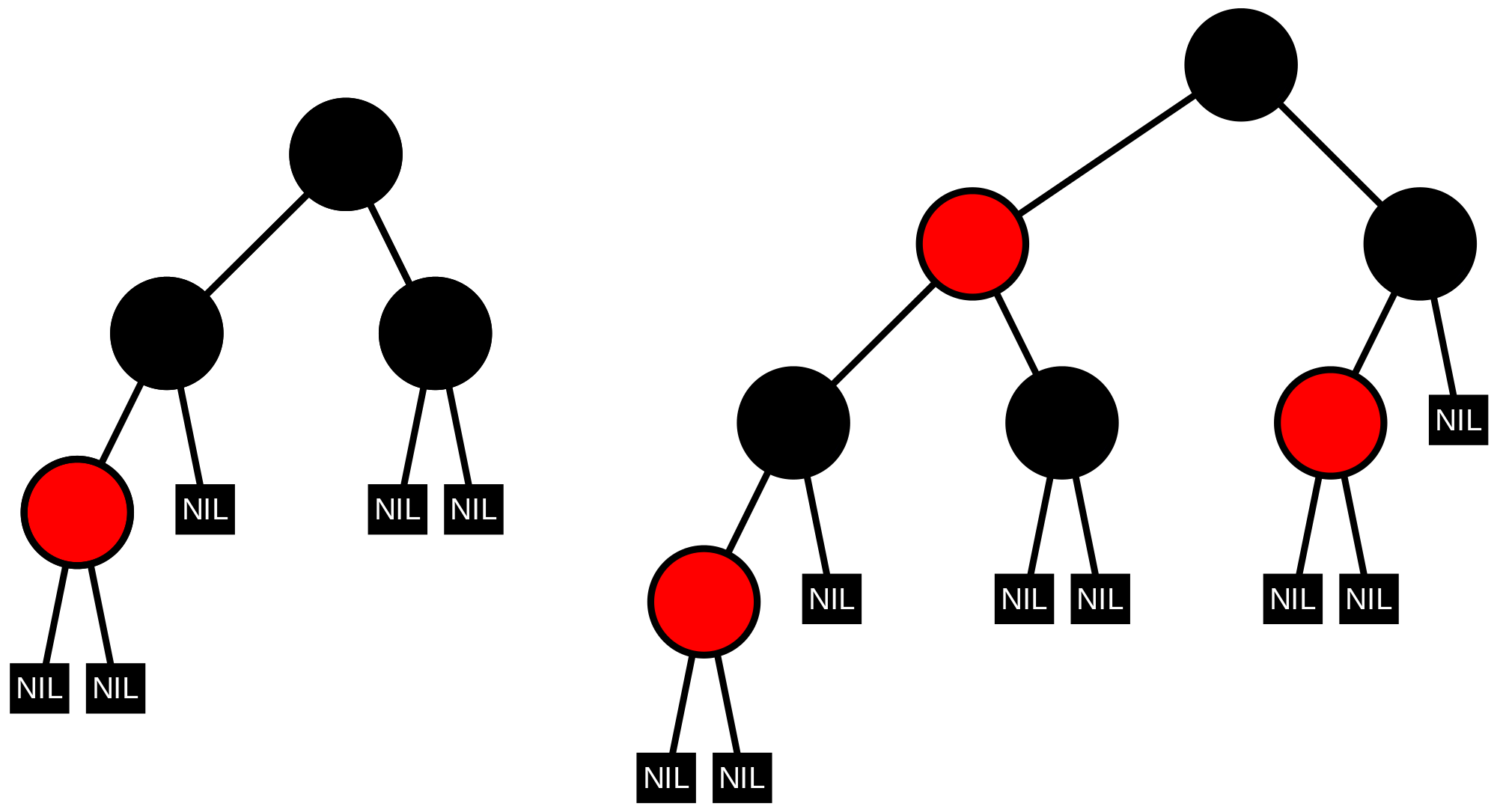
Inserting into Red-Black Trees
A node is initially inserted into a Red-Black Tree just like any Binary Search Tree. The new node is then given a color of red. After that node has been inserted, the tree must be validated to ensure none of the five properties have been violated. If a property has been violated, there are three potential cases requiring either a left-rotation, right-rotation, and/or a recoloring of the nodes. The cases are dependent on the "uncle" of the current node. Specifically, whether the "uncle" node is black or red. For more info on inserting, the three cases can be found here.
Left-Leaning Red–Black Tree
A left-leaning red–black (LLRB) tree is a type of self-balancing binary search tree. It is a variant of the red–black tree and guarantees the same asymptotic complexity for operations, but is designed to be easier to implement.
Properties of Left Leaning Red-Black Trees
All of the red-black tree algorithms that have been proposed are characterized by a worst-case search time bounded by a small constant multiple of log N in a tree of N keys, and the behavior observed in practice is typically that same multiple faster than the worst-case bound, close to the optimal log N nodes examined that would be observed in a perfectly balanced tree.
Specifically, in a left-leaning red-black 2-3 tree built from N random keys: ->A random successful search examines log2 N − 0.5 nodes. ->The average tree height is about 2 log2 N
