By Yung L. Leung
In the previous article “A Step Towards Computing as a Science: Simple Algorithms & Data Structures in JS,” we discussed simple algorithms (linear & binary searches; bubble, selection & insertion sorts) & data structures (array & key-value paired objects). Here, I continue with the concept of complexity and its application to these algorithms & data structures.
Complexity
Complexity is a factor involved in a complex process. Regarding algorithms & data structures, this can be the time or space (meaning computing memory) required to perform a specific task (search, sort or access data) on a given data structure. The efficiency of performing a task is dependent on the number of operations required to complete a task.
Taking out the trash may require 3 steps (tying up a garbage bag, bringing it outside & dropping it into a dumpster). Taking out the trash may be simple, but if you are taking out the trash after a long week of renovation, you may find yourself unable to complete the task due to a lack of space in the dumpster.
Vacuuming a room can require many repetitive steps (turning it on, repeatedly sweeping the vacuum head across a floor & turning it off). The larger a room, the more times you will have to sweep a vacuum head across its floor. Thus, the longer the time it will take to vacuum the room.
So, there is a direct causal relationship between the number of operations performed and the number of elements that are performed on. Having a lot of trash (elements) requires taking it out many times. This can lead to a problem of space complexity. Having a lot of square footage (elements) requires sweeping a vacuum head across a floor many times over. This can lead to a problem of time complexity.
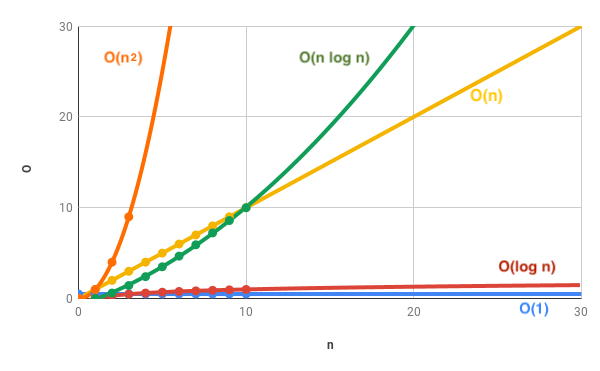
Whether you are taking out the trash or vacuuming a room, you might say that the operation count (O) increases exactly with the number of elements (n). If I have 1 trash bag, I have to take out the trash once. If I had 2 trash bags, I have to perform the same task twice, assuming you physically cannot lift more than one bag at a time. So, the Big-O of these chores is O = n or O = function(n) or O(n). This is a linear complexity (a straight line with a 1 operation: 1 element correspondence). So, 30 operations are performed on 30 elements (yellow line on graph).
This is similar to what happens when considering algorithms & data structures.
Searches
Linear Search
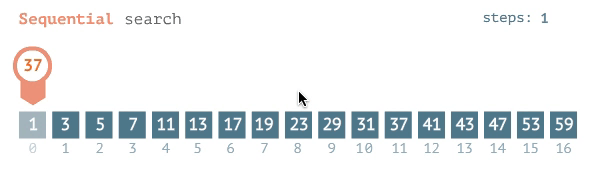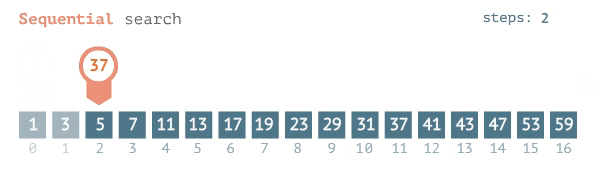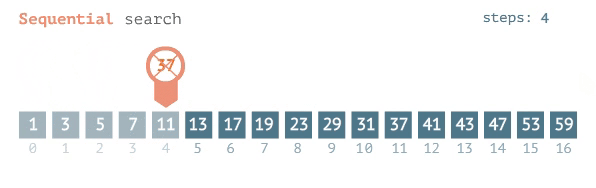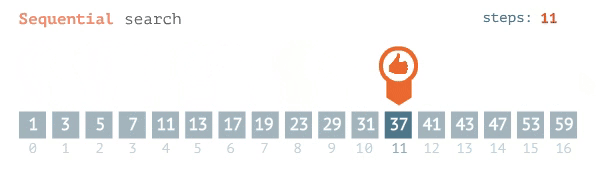
The best case for searching an item in an ordered list, one after another, is a constant O(1), assuming it is the 1st item in your list. So, if the item you are searching for is always listed first, regardless of your list size, you will find your item in an instant. The complexity of your search is constant with the list size. The average to the worst case of this kind of search is a linear complexity or O(n). In other words, for n items, I have to look n times, before I find my item, hence linear search.
Binary Search
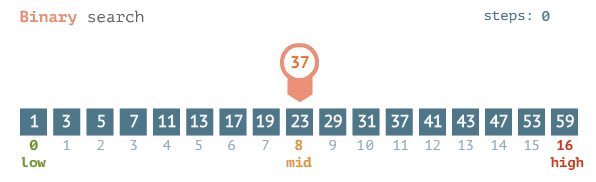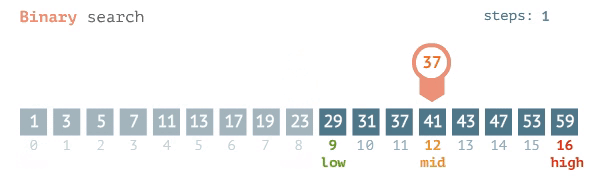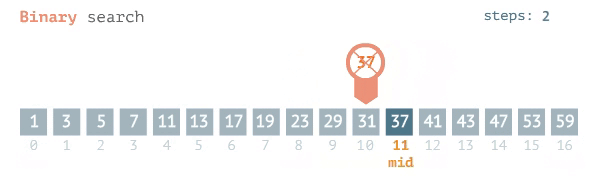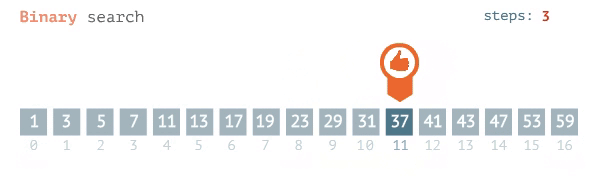
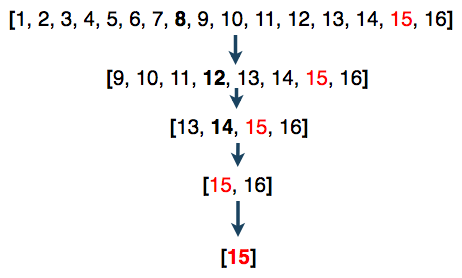
For a binary search, the best case is O(1), meaning the item of your search is located at the midpoint. The worst & average case is log base 2 of n or:
Logarithm or log is a way of expressing an exponent for a given base. So, if there were 16 elements (n = 16), then it would take, at worse case, 4 steps to find the number 15 (exponent = 4).
Or simply: O(log n)
Sorts
Bubble
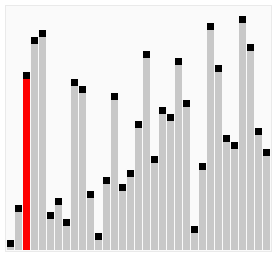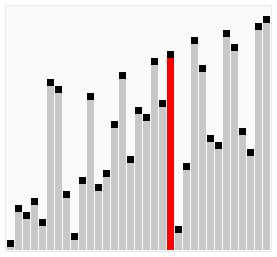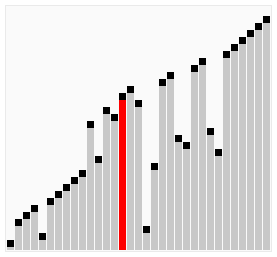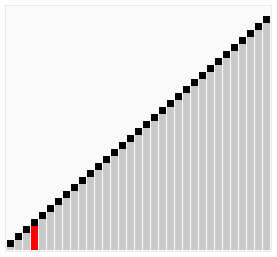
In bubble sort, every item is compared to the rest of the collection to determine the highest value to bubble up. For this reason, on average to worst case, its complexity is O(n²). Think a loop nested within another loop.
So, for each item, you are comparing it to the rest of your collection. This amounts to 16 comparisons (or operations) for 4 elements (4² = 16). The best case is if your collection is almost sorted, except for a single item. This would amount to a single round of comparisons. That is, four comparisons are required to bubble up a member of a four-item collection, which is a complexity of O(n).
Selection

Unlike bubble sort, instead of bubbling up the highest value, selection sort selects the lowest value to swap it to the earliest positions. But, because it requires comparing each item to the rest of the collection, it also has a complexity of O(n²).
Insertion
Unlike the bubble & selection sorts, insertion sort inserts the item into its correct position. But, like the previous sorts, this also requires comparing each item to the rest of the collection, therefore, it has an average to worst case complexity of O(n²). Like the bubble sort, if there is only one item left to sort, it only requires a single round of comparisons to insert the item into its correct position. That is, it has the best case complexity of O(n).
Data Structures
Arrays
Because it takes a single step to access an item of an array via its index, or add/remove an item at the end of an array, the complexity for accessing, pushing or popping a value in an array is O(1). Whereas, linearly searching through an array via its index, as seen before, has a complexity of O(n).
Also, because a shift or unshift of a value to or from the front of an array requires reindexing each element that follows it (i.e. removing an element at index 0 requires relabelling element at index 1 as index 0, and so forth), they have a complexity of O(n). The relabelling is carried through from the start to the end of the array.
Key — Value Paired Objects
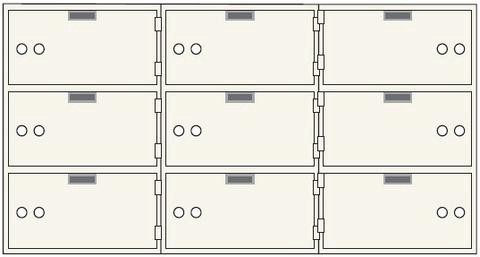
Accessing, inserting or removing a value by using a key is instantaneous, and so, they have a complexity of O(1). Searching through each “deposit box” for a specific item by using every available key is essentially a linear search. And so, it has a complexity of O(n).
Conclusion
Complexity is more than just a topic for discussing established algorithms & data structures. If used wisely, it can be a useful tool for gauging the efficiency of the work you do and the code you create to solve your problems.
Reference:
https://www.udemy.com/js-algorithms-and-data-structures-masterclass/