by Haoxian Chen

The philosophy of programming

Logical thinking === good software

Programming is the new literacy. But how do we write good programs? Here are the recurrent questions we need to solve:

• How do we come up with algorithmic solutions to a problem?
• Then, how do we know the solution actually works?
• Even if we’re sure it works, how do we tell the computer to execute it?

Fun fact — if you have hard time grinding any of these questions, you are actually doing philosophy.

To see why, let’s examine some interesting similarities between programming and philosophical reasoning.

The first principle: you have to think hard.

Computers do nothing smarter than we can do — the difference is, they do it with faster speed.

But they cannot solve an actual problem like “how do I get to my office from home?”

An effective method can (in principle) be carried out by a human being unaided by any machinery except paper and pencil.

— The Church-Turing Thesis

The merit of programming still lies in the reasoning part. That is, translating a real world problem into simple instructions that a computer can execute.

Of course, different programming languages have different levels of semantic abstractions. A Python program might be shorter than its C counterpart. But that just changes the amount of translations. We cannot get rid of the translation work. But we’ll leave this discussion for later.

A programmer’s reasoning flow

Now we are staring at some problem description. We may first look for small-scale input-output examples to understand the problem:

Induction. We need an algorithm that can handle such examples. Now you are doing induction: generalizing principles from experience.

Deduction. How do we know if it works for other unknown input? We do deduction to prove the correctness of our algorithm.

Ontology. We have to maintain data in computer memory. The goal is to make them efficient for the computers to process. In order words, what data structure can best capture the dynamic flow of my information?

Induction again. Then comes the very final stage: debugging. We induce the buggy part of the program from analyzing the unexpected outputs.

An example

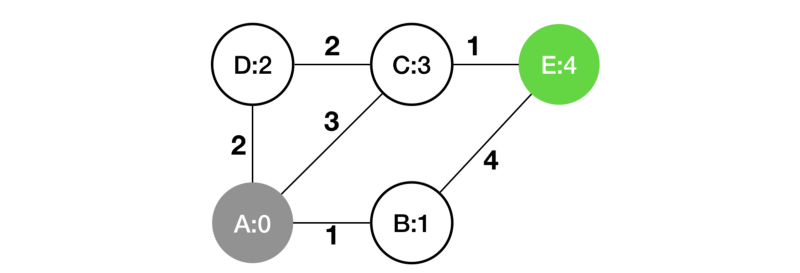
Now let’s examine the above process by following this real example: finding the shortest path from vertex A to vertex E.

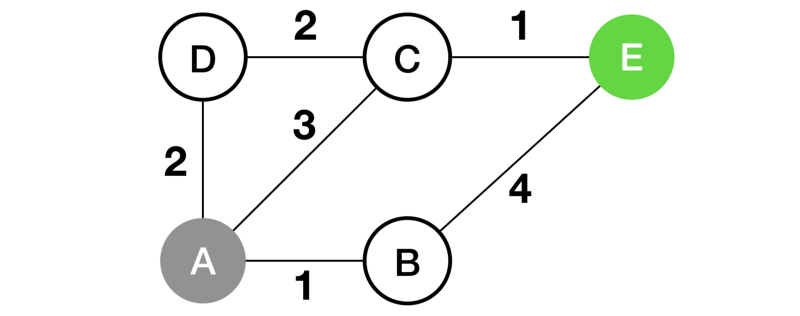
For small scale problems, we can solve them by instincts. Like, it’s very straightforward for us to recognize the solution A-C-E just by looking.

But what about more complex topologies? What about different edge weights?

We need help from computers. Yet it’s not straight forward to tell a computer what to do. There is a gap between how humans think and how a computer works.

The process

1. Generalize principles from experience: algorithms

To tell a computer what to do, we need to first come up with an algorithmic procedure.

Greedy strategies are a natural way to proceed. That is, starting from the source vertex A, and going all the way along the known shortest path. Keep exploring new vertices until we reach destination E. And indeed, this approach satisfies our example.

The intuition is that, along the shortest path to a destination, every intermediate node is visited in the shortest path as well. (Of course this intuition assumes that all edges have positive weights. This may not hold true, depending on the applications. We will discuss this in detail later).

So here is the algorithmic procedure:

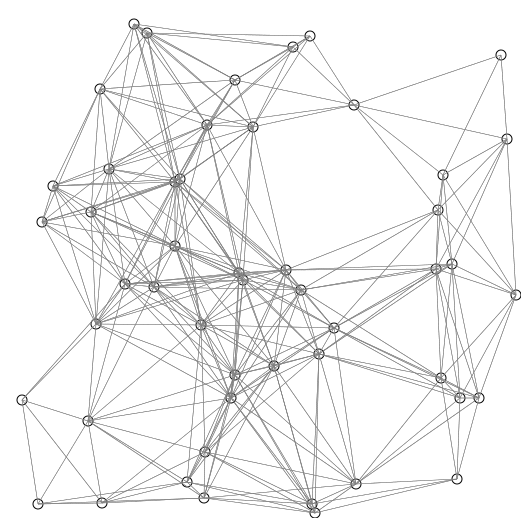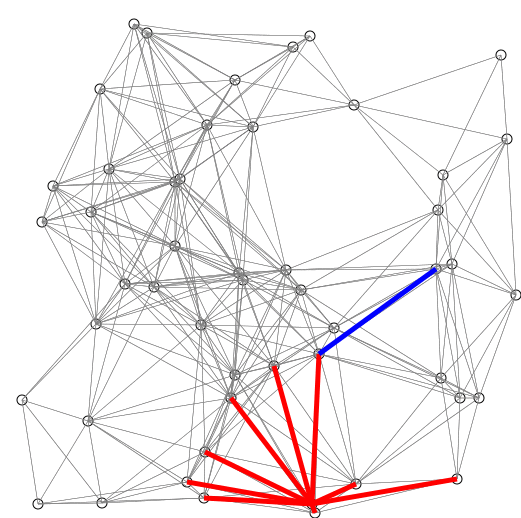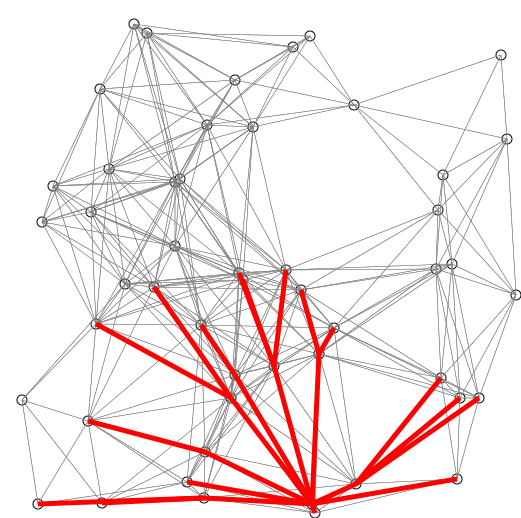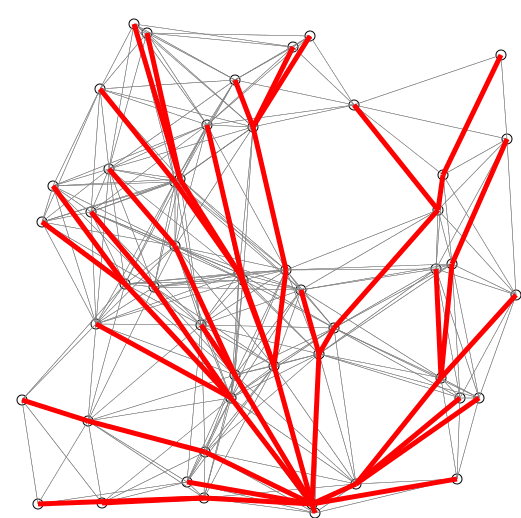
1. Some setup: (1) bookkeep the vertices we have visited: a set (visited), (2) remember the known shortest distances to each vertex that use only discovered vertices: another set distance(u). Every vertex’s distance is initially infinity, except for the source vertex is 0.
2. Now we start exploring: first we visit the vertex that has the known shortest path so far, say it’s u. (Initially it would be the source vertex).
3. When standing at vertex u, we look around the out-going edges. Each edge, say(u,v), gives us a path to vertex v that uses vertex u as the last but only one step. If any of them is indeed a shorter path to v , or the first path we found to v, hooray we can update our set of shortest paths now. Otherwise ignore and keep going.
4. We are done with vertex u, so we add it into our visited set.
5. Go back to step 2, keep exploring until we have visited all vertices.

distance can now tell us the global shortest distances, because it’s used to keep the shortest distances using only visited nodes. And all vertices are visited when the algorithm finishes.

We just reinvented Dijkstra’s algorithm. Of course, there are many other algorithms for finding the shortest path. But the point is, we need a algorithmic procedure to solve the problem.

2. Validate general principles by deduction

How do we make sure the algorithm’s principles are correct? We can either increase our confidence by testing the principle against more input examples, or, more effectively, we can find a rigorous mathematical proof.

Like an a priori proposition in philosophy, the correctness of an algorithm is independent of its execution. In other words, testing cannot guarantee the correctness of algorithms. We need to prove it.

Here’s the basic flow of the proof:

1. For all visited vertices, we find the shortest paths.

2. The destination is visited.

3. Therefore, we find the shortest path to the destination.

Don’t they seem somewhat familiar? Like this:

1. All men are mortal.

2. Socrate is a man.

3. Therefore, Socrate is mortal.

In fact, this is Syllogism, a classic form of deductive reasoning. This is pretty much what logicians are doing.

Another interesting historical fact: the formal concept of computation was first come up by logicians in 1930s. They needed to know if certain logical problems are actually solvable at all (so they could avoid wasting their time solving something unsolvable). To answer that, they come up with the notion of computability.

Later in 1936, Alonzo Church and Alan Turing developed the formal definition of Computability, independently, at the same time. This paper gives a historical review of computation.

The conclusion’s correctness depends on the first two premises. In our proof, the second premise is trivial, since our algorithm is literally visiting all nodes. Yet proving the first premise, that we find the shortest path by the time we visit a node, needs some work.

Mathematical induction can help. It is actually one of the most useful techniques to prove the correctness of a lot of other algorithms.

The general flow goes as follows. First, if an algorithm works on input 0, and second, if the fact that it works on input n implies that it works on input n+1 as well, then it works for all input greater or equal to 0. At this point you are able to guarantee the correctness of your algorithm.

For simplicity, I’ll refer you to this lecture note for the complete proof of this path finding algorithm.

Note that we should not confuse mathematical induction and philosophical induction. By the philosophical definition, mathematical induction is a deductive reasoning process, because it’s correctness is contained in itself, without any external observations.

The lesson is: when we come up with an algorithm, it should be able to handle all possible execution cases.

In practice, going through the rigorous mathematical proof may not be the most efficient strategy. But at least we want to consider as many execution cases as possible, especially the adversarial ones. This practice would improve the robustness of our code.

You may have noticed that, in our example path finding algorithm, it doesn’t work if the edge weight is negative. You can find the reason in this lecture note. To handle a negative-weight graph, you can use the Bellman-Ford algorithm.

3. The ontology problem: data structure

So far we convinced ourselves that we have a correct algorithm. But this is only half the battle.

The next question is, how do we feed the information into computers? Humans like visualized information, like graphs, or histograms. But today’s computers only deal with binary bits.

We need to come up with a data structure that contains the essential information. And it should be efficient for a program to process at the same time.

Let’s continue on our path finding example. A path is an ordered list. But it’s irritating to deal with, compared to an integer. Note that in our algorithm we have to find the shortest path from our set of discovered paths. And then iterate all the way to its end. Seems like we have to dedicate an array or memory to store each path.

Could we do better? Note that in a valid path, consecutive appearances of elements must correspond to an edge in the graph. But, we already have the edge information and they are the same for all paths. Why can’t we get rid of this redundant information?

Well, we can get rid of the list. It turns out that in order to gather the shortest path, the intermediate step is to determine what is the next hop you need to go. All we need to retrieve the shortest path from source A to any target node is just the graph itself, and the shortest distance from A to every node.

A visual representation is in the above picture. This representation is memory efficient. It’s also more efficient for the program to process.

This is how it constructs the shortest path using only the distance vector. Start from the destination vertex, and an empty path. Look up intermediate vertices through incoming edges. Pick the one with the lowest value in distance. Add it to the head of the path. Repeat until we reach the source. This trick actually has a formal notation, called back-tracking.

Philosophers seek for the eternal truth. And programmers want to find out the precise data structure that best captures the dynamics of information. As you see in the path finding example, all it needs to give a shortest path is just a vector, telling you the shortest distances to each vertex. This holds true for any graph, regardless of the number of vertices or edges.

4. A posteriori proposition: debugging

Most programmers have gone through this reasoning tons of times. I bet this is one of the most difficult and time-consuming part of any programming task.

For example, segmentation faults in C programs are often caused by null pointer references. I learned this after dealing with tons of C/C++ segmentation faults. Of course, there are more subtle cases that relate to personal programming habits.

The following example is a syntax mistake made by a programmer. The if condition should have been is_float==1 , but the programmer mistook the logical equal operator == as an evaluation operator =. This will still pass the compiler’s check, because either is correct syntax.

if (is_float = 1) {  // do something}

This is an inductive reasoning process. Your debugging diagnosis only makes sense if you have observed enough program executions.

Here is where the value of practice comes in. No matter what kind of techniques you are learning, you have to gather enough practical data. Otherwise, you wouldn’t have enough experience to conduct induction.

You should keep an eye on the recurrent patterns in your buggy codes. When you find a bug, fixing it is not enough. You need some extra cause-effect analysis on your own programming practice. Ask yourself: is this part of my programming habits particularly vulnerable to these kinds of bug?

So why does it matter?

Programming is not just about writing code, it’s a systematical way of reasoning. Because code, or instructions, is just a means to an end. With the development of program synthesis technique, you may not even bother writing code and debugging yourself. All that matters is if you can tell the computer what to do.

As the first step towards improving your programming skills, this article reveals the underlying reasoning pattern that we may not even recognize when we were programming. Most of us rely on subconscious, automatic reflection to finish most of our day-to-day tasks. But where does improvement come from? It first comes from noticing some fallacy or mistakes we made in our reasoning process.

For practical advice, I recommend this article on how to think like a programmer, and this book on the same topic but with more details.

References

• Computation, Philosophical Issues about. Matthias Scheutz.
• The Church-Turing Thesis.
• Think Like a Programmer: An Introduction to Creative Problem Solving. V. Anton Spraul.