What is a greedy algorithm?
You may have heard about a lot of algorithmic design techniques while sifting through some of the articles here. Some of them are:
- Brute Force
- Divide and Conquer
- Greedy Programming
- Dynamic Programming to name a few. In this article, you will learn about what a greedy algorithm is and how you can use this technique to solve a lot of programming problems that otherwise do not seem trivial.
Imagine you are going for hiking and your goal is to reach the highest peak possible. You already have the map before you start, but there are thousands of possible paths shown on the map. You are too lazy and simply don’t have the time to evaluate each of them. Screw the map! You started hiking with a simple strategy – be greedy and short-sighted. Just take paths that slope upwards the most. This seems like a good strategy for hiking. But is it always the best ?
After the trip ended and your whole body is sore and tired, you look at the hiking map for the first time. Oh my god! There’s a muddy river that I should’ve crossed, instead of keep walking upwards. This means that a greedy algorithm picks the best immediate choice and never reconsiders its choices. In terms of optimizing a solution, this simply means that the greedy solution will try and find local optimum solutions - which can be many - and might miss out on a global optimum solution.
Formal Definition
Assume that you have an objective function that needs to be optimized (either maximized or minimized) at a given point. A Greedy algorithm makes greedy choices at each step to ensure that the objective function is optimized. The Greedy algorithm has only one shot to compute the optimal solution so that it never goes back and reverses the decision.
Greedy algorithms have some advantages and disadvantages:
- It is quite easy to come up with a greedy algorithm (or even multiple greedy algorithms) for a problem. Analyzing the run time for greedy algorithms will generally be much easier than for other techniques (like Divide and conquer). For the Divide and conquer technique, it is not clear whether the technique is fast or slow. This is because at each level of recursion the size of gets smaller and the number of sub-problems increases.
- The difficult part is that for greedy algorithms you have to work much harder to understand correctness issues. Even with the correct algorithm, it is hard to prove why it is correct. Proving that a greedy algorithm is correct is more of an art than a science. It involves a lot of creativity. Usually, coming up with an algorithm might seem to be trivial, but proving that it is actually correct, is a whole different problem.
Interval Scheduling Problem
Let's dive into an interesting problem that you can encounter in almost any industry or any walk of life. Some instances of the problem are as follows:
- You are given a set of N schedules of lectures for a single day at a university. The schedule for a specific lecture is of the form (s time, f time) where s time represents the start time for that lecture and similarly the f time represents the finishing time. Given a list of N lecture schedules, we need to select maximum set of lectures to be held out during the day such that none of the lectures overlap with one another i.e. if lecture Li and Lj are included in our selection then the start time of j >= finish time of i or vice versa .
- Your friend is working as a camp counselor, and he is in charge of organizing activities for a set of campers. One of his plans is the following mini-triathlon exercise: each contestant must swim 20 laps of a pool, then bike 10 miles, then run 3 miles.
- The plan is to send the contestants out in a staggered fashion, via the following rule: the contestants must use the pool one at a time. In other words, first one contestant swims the 20 laps, gets out, and starts biking.
- As soon as this first person is out of the pool, a second contestant begins swimming the 20 laps; as soon as he or she is out and starts biking, a third contestant begins swimming, and so on.
- Each contestant has a projected swimming time, a projected biking time, and a projected running time. Your friend wants to decide on a schedule for the triathlon: an order in which to sequence the starts of the contestants.
- Let's say that the completion time of a schedule is the earliest time at which all contestants will be finished with all three legs of the triathlon, assuming the time projections are accurate. What is the best order for sending people out, if one wants the whole competition to be over as soon as possible? More precisely, give an efficient algorithm that produces a schedule whose completion time is as small as possible
The Lecture Scheduling Problem
Let's look at the various approaches for solving this problem.
Earliest Start Time First i.e. select the interval that has the earliest start time. Take a look at the following example that breaks this solution. This solution failed because there could be an interval that starts very early but that is very long. This means the next strategy that we could try would be where we look at smaller intervals first.
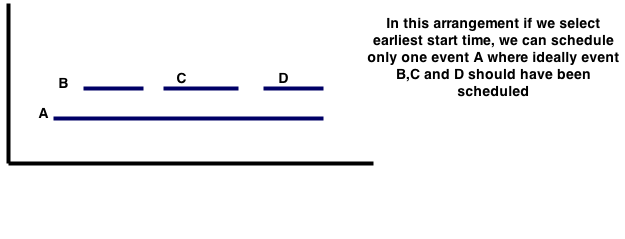
Smallest Interval First i.e. you end up selecting the lectures in order of their overall interval which is nothing but their finish time - start time . Again, this solution is not correct. Look at the following case.
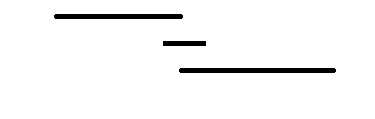
You can clearly see that the shortest interval lecture is the one in the middle, but that is not the optimal solution here. Let's look at yet another solution for this problem deriving insights from this solution.
Least Conflicting Interval First i.e. you should look at intervals that cause the least number of conflicts. Yet again we have an example where this approach fails to find an optimal solution.
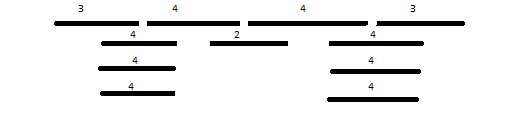
The diagram shows us that the least confliciting interval is the one in the middle with just 2 conflicts. After that we can only pick the two intervals at the very ends with conflicts 3 each. But the optimal solution is to pick the 4 intervals on the topmost level.
Earliest Finishing time first. This is the approach that always gives us the most optimal solution to this problem. We derived a lot of insights from previous approaches and finally came upon this approach. We sort the intervals according to increasing order of their finishing times and then we start selecting intervals from the very beginning. Look at the following pseudo code for more clarity.
function interval_scheduling_problem(requests)
schedule \gets \{\}
while requests is not yet empty
choose a request i_r \in requests that has the lowest finishing time
schedule \gets schedule \cup \{i_r\}
delete all requests in requests that are not compatible with i_r
end
return schedule
end
When do we use Greedy Algorithms
Greedy Algorithms can help you find solutions to a lot of seemingly tough problems. The only problem with them is that you might come up with the correct solution but you might not be able to verify if its the correct one. All the greedy problems share a common property that a local optima can eventually lead to a global minima without reconsidering the set of choices already considered.
Greedy Algorithms help us solve a lot of different kinds of problems, like:
