A rational number is any number that can be written as a fraction, where both the numerator (the top number) and the denominator (the bottom number) are integers, and the denominator is not equal to zero.
In other words, a rational number can be expressed as p/q, where p and q are both integers and q ≠ 0.
In this article, we'll go over what whole numbers and integers are, cover different types of rational numbers, and learn how to determine if a number is rational or not.
What Are Whole Numbers and Integers?
Before getting into integers, it would be helpful to review what whole numbers are.
Whole Numbers
A whole number is any number from 0 up to infinity: 0, 1, 2, 3, 4, 5, ...
Note that whole numbers are just that – whole. They do not include decimals or fractions, and since they start from 0 and go up, all whole numbers are positive.
So 11, 0, 2014, and 938,840,123 are all whole numbers.
-2, 3.8, and 13/100 are not whole numbers.
Integers
Integers are exactly like whole numbers, but can also include negative numbers: ..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...
12, -33, and 0 are all integers.
But 1/2, 3.14, and -3.333 are not integers.
Rational Numbers
Again, a rational number is any number that can be expressed as a fraction, where both the numerator and denominator are integers, and the denominator is not 0:
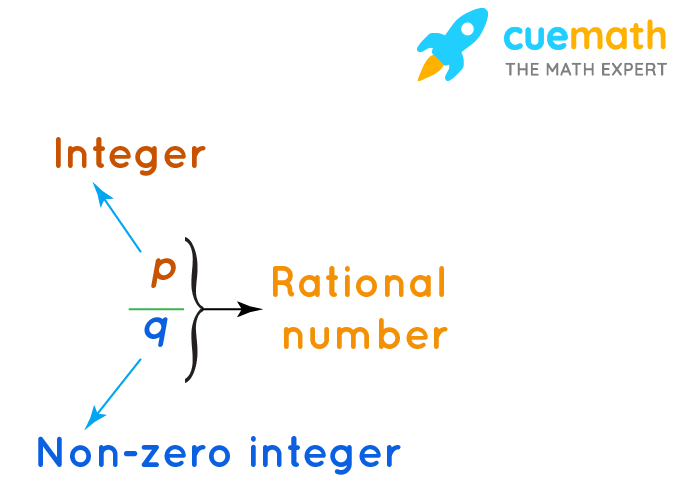 Source: Rational Numbers
Source: Rational Numbers
Some examples of rational numbers include:
- 3/4 (three quarters)
- 1/2 (one half)
- 5/8 (five eighths)
According to Wikipedia, the term ratio "is derived from rational".
So if a number can be expressed cleanly as a fraction, or a ratio between two integers, then it's a rational number. And if a number can't be expressed this way, then it's an irrational number.
Types of Rational Numbers
Though you learned what rational numbers are earlier in the article, it's helpful to break them up into broad categories, and look at different examples.
There are four types of rational numbers:
- integers
- fractions made up of integers
- terminating decimal numbers
- non-terminating decimal numbers with infinitely repeating patterns
Integers
Any integer can be converted cleanly into a fraction, and is a rational number.
For example, 3 can be expressed as 3/1. And since both the numerator (3) and denominator (1) are integers, and the denominator is not 0, then 3 is a rational number.
This works for negative integers like -2 (or -2/1) and -2006 (or -2006/1).
The number 0 is also a rational number, because it can be converted into a fraction. For example, 0/1, 0/-4, and 0/18,572 are all valid fractions, and meet the definition of a rational number.
Fractions Made up of Integers
Any fraction made up of integers is a rational number, as long as the denominator is not 0.
For example, 1/3, -5/3, and 27/-463 are all rational numbers.
Terminating Decimal Numbers
Any decimal number that terminates, or ends at some point, is a rational number.
For example, take the decimal number 0.5. This can be converted to 1/2, which means its a rational number.
Even longer terminating decimal numbers can be cleanly converted into fractions. For instance, 0.0001 can be expressed as 1/10,000, meaning that it's a rational number.
As long as a decimal number eventually terminates, without rounding or approximation, it's a rational number.
Non-terminating Decimal Numbers With Infinitely Repeating Patterns
Decimal numbers that go on forever with repeating patterns are rational numbers. But this is a bit tricky, because the pattern must repeat infinitely.
For example, take the number 0.33333... Even though this is often simplified as 0.33, the pattern of 3's after the decimal point repeat infinitely. This means that the number can be converted into the fraction 1/3, and is a rational number.
But what about a more complicated number, like 0.142857142857...? Again, the 142857 pattern after the decimal repeats infinitely, and the number can be converted to 1/7, which is rational.
However, there are decimal numbers that go on infinitely that do not contain repeating patterns. These types of numbers are not rational numbers, and are known as irrational numbers.
Irrational Numbers
Any number that does not meet the definition of a rational number is an irrational number.
Numbers like pi (π = 3.1415926536...) and many square roots (√2 = 1.41421356237...) have digits that go past the decimal point infinitely. But they don't contain infinitely repeating patterns, so they're considered irrational.
For example, while pi is often shortened to 3.14159, that's just an approximation. At the time of writing, the world record for the number of digits of pi that have been calculated is 62.8 trillion. And as computing power increases, so will that record.
But as far as anyone can tell, within those endless digits there are no repeating patterns, so pi is considered an irrational number.
Thanks for Reading
If you found this article on rational numbers helpful, consider sharing it so more people can benefit from it.
Also, feel free to reach out on Twitter and let me know what you think.

