by Pramod Sripada

Infix Expressions VS Postfix Expressions, and How to Build a Better JavaScript Calculator

If you want to make your Simple Calculator a lot smarter, this post is for you.

You might asking, “What’s wrong with my simple calculator.” Well, it may do all the operations correctly, but the sequence in which it does them is probably wrong.

The simple calculator contains just four operations: addition, subtraction, division and multiplication. Many of us might have studied in high school about the precedence of operators: division and multiplication have the same priority, and have higher priority than addition and subtraction, which have the same priority.

A quick recap of operator precedence can be found here: http://www.math.utah.edu/online/1010/precedence/.

The reason I am stressing operator precedence is because a simple calculator performs most of the calculations wrong. For example, 1+2x3 should be equal to 7 according to a normal calculator, but the simple calculator gives a result of 9.

The reason simple calculator does it all wrong is because it just multiplies the two operands, with the operator between them, and produces the result.

We just can’t blame the simple calculator. After all, it was meant to be simple. So now you might start thinking on how to rearrange the operators, so as to get the correct result. Yes, you are on the right track. For that, we need to know about two more concepts in computer science: Infix expressions and Postfix expressions.

In simple words, the arithmetic expressions that we understand are Infix expressions and the arithmetic expression that the computer understands are Postfix expressions.

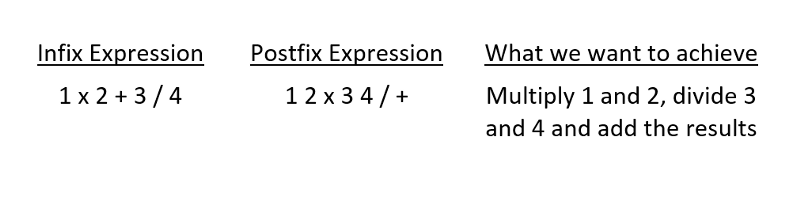
Both the infix and postfix expressions create the same results. It’s just humans are used to solving infix expressions, and computers are used to solving postfix expressions.

Another key feature in the postfix expression is that it contains operators succeeding the operands according to precedence, which makes it easy for the computer to evaluate them using stacks, and produce the correct result.

By now you must be thinking about how to convert the infix expression entered by your user into a postfix expression. There is an algorithm that converts an infix expression into a postfix expression that can be found here.

Here’s what this process looks like:

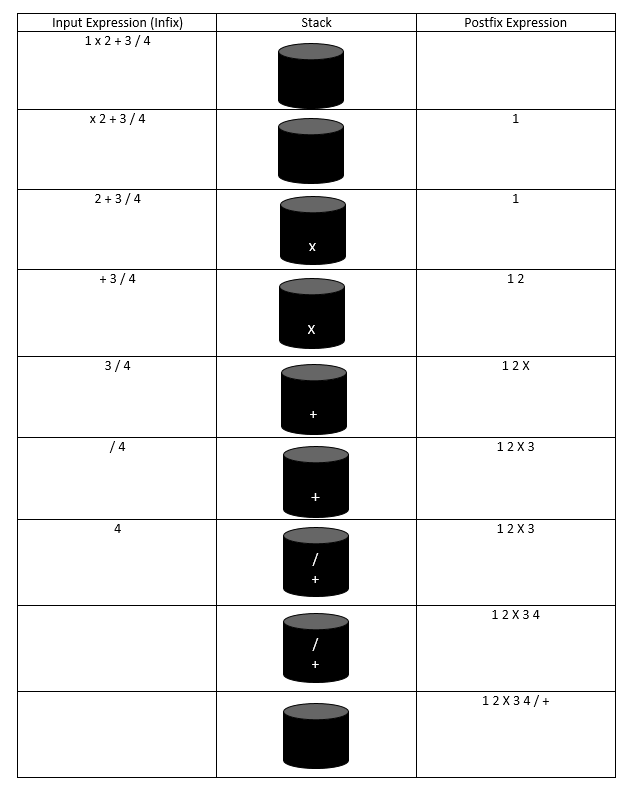
The postfix expression should be evaluated by an algorithm, which can be found here. It is similar to the evaluation done by a simple calculator, except that the operators succeed the operands in postfix expressions.

Eventually, the primary motive of converting an infix expression into a postfix expression is to preserve the precedence of the operators while the computer evaluates the expression.

Check out my fully functional calculator that incorporates these principles here.