Original article: What is Big O Notation Explained: Space and Time Complexity

빅오 표기법을 완벽히 이해하시나요? 만약 그렇다면 이 글이 면접 전에 기억을 환기 시켜주길 바랍니다.
그렇지 않다면, 걱정할 필요 없습니다. 컴퓨터 과학 분야에 함께 도전해 볼까요?

알고리즘 관련 코스들을 들어본 적이 있다면 빅오 표기법에 대해 이미 들어봤을 가능성이 큽니다. 들어보지 못한 분들을 위해,
빅오 표기법이 무엇인지 부터 다뤄보겠습니다. 그 후에 뒷부분으로 갈 수록 조금 더 심화적인 내용을 다룰 것입니다.

빅오 표기법은 알고리즘의 효율성을 분석하기 위해 컴퓨터 공학자들이 쓰는 가장 기본적인 도구들 중 하나 입니다. 소프트웨어 엔지니어들도 이 개념을 잘 이해하고 있다면 도움이 될 것입니다.

이 글의 독자분들은 이미 코딩을 조금 해보신 분들이라는 전제하에 글을 썼습니다. 또한 고등학교 수준 수학의 기본적인 개념을 알아야 심화 내용을 이해할 수 있을 것입니다.
따라서 이런 지식이 전혀 없으신 분들에게는 조금 어려울 수 있다는 점을 양해 부탁드립니다.
이제 준비가 되셨다면, 시작해 보겠습니다.

이 글에서는 빅오 표기법에 대해 자세히 다룰 것입니다. 먼저 한 예시 알고리즘을 보면서 시작하겠습니다. 그런 다음에는 공식 개념을 이해하기 위해 조금 더 수학적인 개념을 알아보겠습니다.
일반적인 빅오 표기법의 변형형들도 살펴볼 것 입니다. 마지막으로 실질적인 상황에서 빅오 표기법이 어떤 한계들을 가질 수 있는지 보겠습니다. 목차는 아래와 같습니다.

목차

1. 빅오 표기법이 무엇이며 왜 중요할까
2. 빅오 표기법의 공식적인 정의
3. 빅오(Big-O), 리틀오(Little-o), 오메가(Omega)와 세타(Theta)
4. 전형적인 빅오(Big-O)간의 복잡도 비교
5. 시간과 공간의 복잡도
6. 최선, 평균, 최악, 예상 복잡도
7. 빅오(Big-O)가 상관 없는 이유
8. 결론

시작해 봅시다.

1. 빅오 표기법이 무엇이며 왜 중요할까

“빅 오 표기법은 인자가 특정한 값이나 무한대로 향할 때 함수의 극한적인 동작을 설명하는 수학적인 표기법입니다. 이것은 폴 바흐만, 에드문드 란다우 등이 고안한 기호 체계 중 하나로, 박만-란다우 표기법 또는 점근적 표기법이라고 불리는 체계에 속합니다.”

위키피디아 영문 페이지에 나온 빅오 표기법의 정의
간단히 말하자면 빅오 표기법이란 코드의 복잡도를 대수학 개념을 이용해 표현하는 것입니다.

일반적인 예, **O(n²)**를 보며 빅오 표기법이 무엇인지 살펴보겠습니다. **"빅 오 제곱"**이라고 읽습니다. 여기에 있는 **"n"**은 입력값의 크기를 나타냅니다.
그리고 **“O()”**안에 있는 함수 **“g(n) = n²”**는 입력값의 크기에 따라 얼마나 알고리즘이 복잡해지는지를 알려줍니다.

선택 정렬 알고리즘은 O(n²)의 복잡도를 갖고 있는 전형적인 알고리즘 입니다. 선택 정렬 알고리즘이란 주어진 배열을 반복해서 따라가며 각 인덱스 i에 있는 값이 그 정렬에서 i 번째로가장 크거나 작은 값이 되도록 하는 것 입니다.
아래의 CODEPEN에 이것을 시각화 시킨 예시가 있습니다.

이 알고리즘은 아래와 같은 코드로 나타낼 수 있습니다. 어떤 배열에서 ~번째에 있는 값이 그 배열의 ~번째로 작은 값이 되도록 하기 위해서 먼저 for 반복문을 이 배열에
실행합니다. 그리고 각 값에 또 다른 for 반복문을 이용해서 남은 배열 구간에서 가장 작은 값을 찾아냅니다.

SelectionSort(List) {
  for(i from 0 to List.Length) {
    SmallestElement = List[i]
    for(j from i to List.Length) {
      if(SmallestElement > List[j]) {
        SmallestElement = List[j]
      }
    }
    Swap(List[i], SmallestElement)
  }
}

이 예시에서 우리는 변수 **List**를 입력값으로 합니다. 그렇기 때문에 입력값의 크기 n은 **List 라는 배열안에 있는 값들의 숫자**가 됩니다.
if 조건문에서 조건식 안에 들어있는 구문이 실행되는데 일정한 시간이 걸린다고 가정해봅시다. 그렇다면 위의 SelectionSort 함수에서 몇번이나 코드가
실행되는지를 분석한다면 이 함수의 빅오 표기법을 알 수 있습니다.

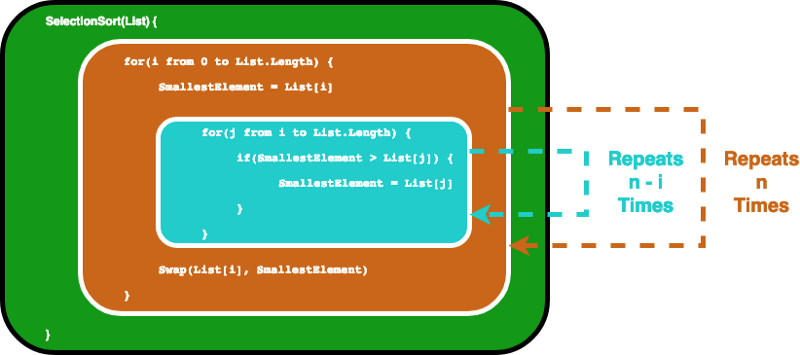
일단 처음에는 가장 안에 있는 for 반복문은 그 안의 코드를 n번 실행하게 됩니다. 그 후에 **i**가 증가하게 되면 안에 있는 for 반복문은 n-1번 실행됩니다.
계속 이런식으로 결국 이 두개의 for 반복문은 마지막으로 조건이 만족되는 순간에 다다릅니다.

선택정렬 반복문 그림

이 반복문으로 우리는 총 합계를 구할 수 있습니다. 고등학교 수준의 수학으로 우리는
안에 있는 반복문이 1+2...+n 번 반복한다는 것을 알 수 있고 이것은 n(n-1)/2 번 이라는 식으로 나타낼 수 있습니다. 이 식을 풀게 되면 n²/2-n/2 라는 식을 얻게 됩니다.

빅오 표기법을 계산할 때에는 최고차항만 신경쓰고 나머지 계수들은 신경쓰지 않습니다. 그러므로 여기에서 우리는 점근 표기법의 값으로 n² 을 얻게 됩니다.
이것은 O(n²)로 표시하고 *"빅오 n의 제곱(Big O squared)*이라고 읽습니다.

그렇다면 이 **최고차항**이라는 것은 무엇일까요? 그리고 나머지 계수들에 대해서는 왜 신경쓰지 않아도 될까요?
이 이유들에 대해서는 하나씩 차근차근 알아보도록 하겠습니다. 처음에는 이해하기 어려울 수 있으나 다음 부분을 읽게 된다면 훨씬 더 이해가 잘 될 수 있을 것입니다.

2. 빅오 표기법의 공식적인 정의

옛날 옛적 어떤 인도의 왕은 한 지혜로운 사람에게 상을 내리고 싶어 했습니다. 이 지혜로운 사람은
다른 것이 아닌 체스 판을 가득 채울 만큼의 밀알을 원했습니다.

하지만 이 사람의 조건은 이러했습니다. 체스 판의 첫번째 칸에는 1 알의 밀알을, 두번째 칸에는 2알의 밀알을, 그리고 그 다음 칸에는 4알의 밀알을...이런 식으로 체스 판의 각 칸은 바로 이전 칸에 있는 밀알의 제곱한 양으로 채워지기를 바랬습니다. 순진한 왕은 흔쾌히 수락했습니다. 아주 쉽게 들어줄 수 있는 요구라고 생각했습니다. 직접 체스 판을 이런 식으로 채워보기 전까지는 말이죠.

밀알과 체스판, 이미지 출처 위키피디아

이 왕은 지혜로운 사람에게 얼마만큼의 밀알을 주어야 했을까요? 체스 판에는 8 곱하기 8 만큼의 칸이 있습니다. 총 64칸인 셈 입니다. 그렇다면 마지막 칸에는 총 2⁶³ 알 만큼의 밀알이 있어야 합니다.
이를 인터넷에서 계산을 해본다면 전체 체스판에 대해 얻을 수 있는 밀알은 1.8446744*10¹⁹라는 결과가 나옵니다. 간단히 말하자면 이는 18에 0이 18개가 붙은 숫자입니다.

밀알 한 알이 0.01그램이라고 가정해본다면 총 184,467,440,737톤의 밀알을 얻게 되는 것입니다. 1천 8백 4십억톤이라면, 꽤 무거운 것이 맞죠?

보는 것처럼, 기하급수적 증가에서는 뒤로 갈 수록 숫자가 아주 빠른 속도로 커지게 됩니다. 이는 컴퓨터 알고리즘에서도 마찬가지 입니다. 무엇을 실행하기 위해 드는 노력이 입력값이 커짐에 따라 기하급수적으로 증가하게 된다면 끝에는 아주 큰 숫자가 될 수 있습니다.

곧 나오겠지만 2ⁿ의 증가률은 n² 보다 훨씬 빠릅니다. n = 64 라고 한다면 64의 제곱은 4096 입니다. 하지만 그 숫자를 거듭제곱에 넣어서 2⁶⁴ 가 된다면, 표기하기도 어려운 크기의 숫자가 됩니다.

증가율을 계산할 때 최고차항만을 보는 이유가 바로 이것입니다. 그리고 입력값 크기에 따른 시간 증가를 분석할 때에는 입력값 증가와는 관계 없이 -입력값이 증가함에 따라 같이 증가하는 것이 아니므로- 그 숫자만큼만 곱해지게 되는 계수는 우리에게 유용한 정보를 갖고 있지 않습니다.

빅오 표기법 의 공식적인 정의는 아래와 같습니다.

워싱턴 대학의 CSE 373 슬라이드

(역주: 슬라이드에 쓰여진 내용은 다음과 같습니다.

• 빅오는 점근선의 상한 범위를 찾는 것이다.
• 빅오의 공식적인 정의는
  f(N) = O(g(N)), 양수인 상수 c가 있다면, N₀ 는 다음과 같다.
  모든 N ≥ N₀ 에 대해 f(N) ≤ c * g(N) 이다.
• 우리는 N이 커질때에 f가 어떻게 증가하는지를 구하고 싶다.
• 작은 N이나 상수 인자는 고려하지 않는다.
• 용어: "f(N)은 g(N)이 증가하는 만큼만 증가한다."
  )

공식적인 정의는 수학적 증명을 해야할 때 유용합니다. 예를 들면 선택 정렬의 시간 복잡도는 이 전 부분에서 봤던 것 처럼 f(n) = n²/2-n/2 와 같은 함수로 나타낼 수 있습니다.

만약 g(n)함수를 n²이라고 한다면, 계수 c = 1 와 N₀ = 0 을 알 수 있습니다. 여기에서 N > N₀ 라는 조건이 만족하는 한, N² 는 N²/2-N/2 보다 항상 큰 값이 됩니다.
이는 각 함수들에서 N²/2를 빼봄으로써 쉽게 증명할 수 있습니다. 그렇다면 N²/2 > - N/2 는 N > 0 라는 조건에서 참이라는 걸 알 수 있습니다. 그러므로 f(n) = O(n²), 즉 선택 정렬에서는 "제곱의 시간이 걸린다(big O squared)"고 하는 결론을 낼 수 있는 것입니다.

여기에서 한가지 trick을 눈치 채셨을 수도 있습니다. 만약 g(n)을 아주 빠르게 증가하도록 한다면 O(g(n))는 항상 충분히 큰 값이 됦 것입니다. 예를 들어 어떤 다항함수가 있다면 여기에서는
O(2ⁿ)라고 할 수 있습니다. 왜냐하면 2ⁿ 는 결국에는 어떤 다항식보다 더 크게 증가하기 때문입니다.

수학적으로는 맞는 말입니다. 하지만 일반적으로 빅오에 대해 말할 때에는 함수의 **엄격한 제한(tight bound)**에 대해 알아야 합니다. 계속해서 다음 부분을 읽어나가면 더욱 이해 하는데에 도움이 될 겁니다.

먼저 다음 질문으로 이때까지 얼마나 이해하고 있는지 시험해 봅시다. 정답은 후에 나오는 섹션에 있습니다. 정답을 보지 않고 생각해 보세요.

질문: 어떤 이미지가 2D 배열의 픽셀로 표현되어 있다. 만약 중첩 for문을 사용해서 모든 픽셀들을 반복하게 된다면 (그 뜻은 바깥의 for문이 모든 열-column-을 따라 반복할 때에
안에 있는 for문은 모든 행-row-을 따라 반복한다는 것이다.) 여기에서 이미지가 함수의 입력값(input)이라면 이 함수의 시간 복잡도는 무엇일까?

3. 빅오(Big O), 리틀오(Little O), 오메가(Omega) & 세타(Theta)

빅오: 어떤 상수 c와 N₀에 대해 N > N₀ 이면서 f(N) ≤ cg(N) 인 조건을 만족할 때 “f(n) 는 O(g(n)) 이다”. (필요충분조건으로, 역도 참이다.)
오메가: 어떤 상수 c와 N₀에 대해 N > N₀ 이면서 f(N) ≥ cg(N) 인 조건을 만족할 때 “f(n) 는 Ω(g(n)) 이다”. (필요충분조건으로, 역도 참이다.)
세타: f(n) 는 O(g(n)) 이면서 f(n) 는 Ω(g(n)) 인 조건을 만족할 때 “f(n) 는 Θ(g(n)) 이다”. (필요충분조건으로, 역도 참이다.)
리틀오: f(n) 는 O(g(n)) 이면서 f(n) 는 Θ(g(n)) 가 아닌 조건을 만족할 때 “f(n) 는 o(g(n)) 이다”. (필요충분조건으로, 역도 참이다.)
-빅오, 오메가, 세타, 리틀오의 공식적인 정의
이것을 풀어서 다시 설명하자면 다음과 같습니다.

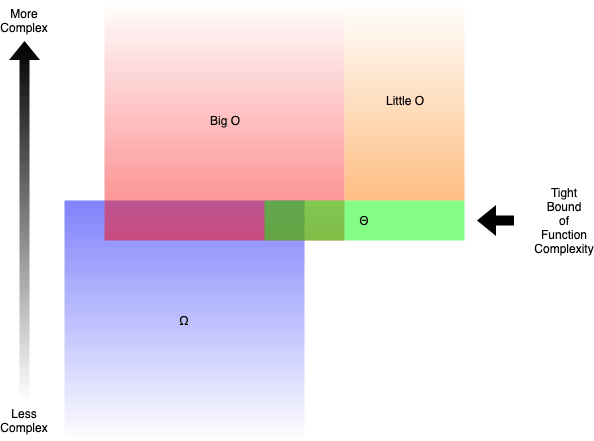
• 빅오 (O()) 는 복잡도의 윗쪽 범위를 나타낸다.
• 오메가 (Ω()) 는 복잡도의 아랫쪽 범위를 나타낸다.
• **세타 (Θ()) ** 는 복잡도의 정확한 범위를 나타낸다.
• 리틀오 (o()) 는 복잡도의 정확한 범위를 제외한 윗쪽 범위를 나타낸다.

빅오, 오메가, 세타, 리틀오의 관계 그래프

예를 들면 g(n) = n² + 3n is O(n³), o(n⁴), Θ(n²) and Ω(n) 와 같은 함수로 나타낼 수 있습니다. 하지만
간단하게 Ω(n²) 나 O(n²) 로 표현해도 맞습니다.

일반적으로 빅 오(Big O)에 대해 이야기할 때, 우리가 실제로 의미하는 것은 세타(Theta)입니다. 분석 범위보다 훨씬 큰 상한을 제시하는 것은 의미가 없습니다. 이는 부등식을 풀 때 ∞를 큰 쪽에 놓으면 거의 항상 옳은 것과 마찬가지 입니다.

하지만 우리는 어떻게 다른 함수들 중에서 어떤 함수가 더 복잡한지를 결정할까요? 다음 섹션에서는 그것에 대해 자세히 배우게 될 것입니다.

4. 전형적인 빅 오(Big O)간의 복잡도 비교

특정 함수 g(n)의 빅 오(Big O)를 찾으려 할 때, 우리는 함수의 **지배적인 항(dominant term)**에만 관심이 있습니다. 지배적인 항이란 가장 빨리 증가하는 항을 말합니다.

예를 들어, n²은 n보다 더 빨리 증가하기 때문에, g(n) = n² + 5n + 6과 같은 함수는 빅 오(n²)가 됩니다. 미적분학을 공부한 적이 있다면, 분수 다항식의 극한값을 찾는 데에 사용되는 간략한 방법과 매우 유사합니다. 극한값을 찾을 때, 분자와 분모의 지배적인 항만 고려하면 되는 것과 같습니다.

빅오를 보는 또 다른 방법, 이미지 출처는 스택 오버플로우

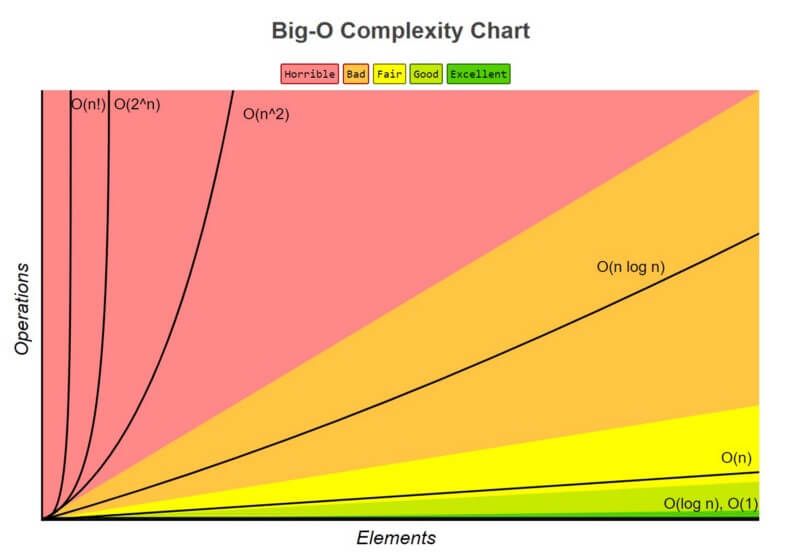
하지만 어떤 함수가 다른 함수보다 더 빠르게 증가할까요? 이에 대해 꽤 많은 규칙이 있습니다.

빅 오(Big O) 치트시트에서의 복잡도 증가 그림 예시

1. O(1)이 가장 적은 복잡도를 가집니다.

O(1)은 종종 **"상수 시간(constant time)"**이라고 불리며, 만약 문제를 O(1)로 해결할 수 있는 알고리즘이 있다면, 그것이 최선일 가능성이 높습니다. 일부 상황에서는 복잡도가 O(1)을 초과할 수도 있습니다. 그런 경우에는 O(1/g(n)) 상대 알고리즘을 찾아서 분석할 수 있습니다. 예를 들어, O(1/n)은 O(1/n²)보다 더 복잡합니다.

(역주: "상대 알고리즘(relative algorithm)"이란, 두 가지 이상의 알고리즘 중에서 더 효율적인 알고리즘을 선택하기 위해, 비교 대상이 되는 알고리즘을 의미합니다. 복잡도 분석에서, 하나의 알고리즘을 더 나은 다른 알고리즘과 비교하여 상대적인 성능을 평가하기 위해 사용됩니다. O(1/g(n))은 O(g(n))의 역수로, 복잡도가 낮을수록 더 나은 알고리즘이라는 의미를 갖습니다.)

2. O(log(n))는 O(1)보다는 더 복잡하지만 다항식보다는 덜 복잡합니다.

복잡도는 종종 분할 정복 알고리즘과 관련이 있기 때문에, O(log(n))는 일반적으로 정렬 알고리즘에 도달할 수 있는 좋은 복잡도입니다. O(log(n))는 O(√n)보다 덜 복잡합니다. 왜냐하면 제곱근 함수는 지수가 0.5인 다항식으로 간주될 수 있기 때문입니다.

3. 다항식의 복잡도는 지수가 증가함에 따라 증가합니다.

예를 들어, O(n⁵)는 O(n⁴)보다 더 복잡합니다. 이전 섹션에서는 다항식의 예를 많이 다루었는데, 이는 그 복잡성이 간단하기 때문입니다.

4. 계수가 n의 양의 배수인 경우, 지수 함수의 복잡도는 다항식의 복잡도보다 큽니다.

O(2ⁿ)는 O(n⁹⁹)보다 복잡하지만, O(2ⁿ)은 실제로 O(1)보다 덜 복잡합니다. 지수와 로그의 밑(base)으로 일반적으로 2를 사용하는 이유는 컴퓨터 과학에서 일반적으로 이진(binary) 표현을 사용하기 때문입니다. 그러나 계수를 변경함으로써 지수를 변경할 수 있습니다. 로그의 밑은 별도로 지정되지 않은 경우 2로 간주됩니다.

5. 팩토리얼(factorial)은 지수(exponential)보다 더 높은 복잡도를 가집니다.

만약 이유에 대해 관심이 있다면 감마 함수를 검색해보세요. 감마 함수는 팩토리얼의 해석적 연속 확장입니다. 간단한 증명은 팩토리얼과 지수 함수가 같은 수의 곱셈을 갖지만, 곱해지는 수가 팩토리얼의 경우 커지고, 지수 함수의 경우에는 일정하게 유지된다는 것입니다.
(역주: 해석적 연속 확장(Analytic Continuation)은 어떤 함수가 정의되어 있던 범위를 그보다 더 큰 범위로 확장하여 정의하는 것을 말합니다.)

6. 항을 곱하는 것

곱셈을 할 때, 복잡성은 원래 것보다 더 커질 것이지만 더 복잡한 것을 곱하는 경우보다 더 커지지는 않습니다. 예를 들어, O(n * log(n))는 O(n)보다 더 복잡하지만 O(n²)보다는 덜 복잡합니다. 왜냐하면 O(n²) = O(n * n)이고, n은 log(n)보다 더 복잡하기 때문입니다.

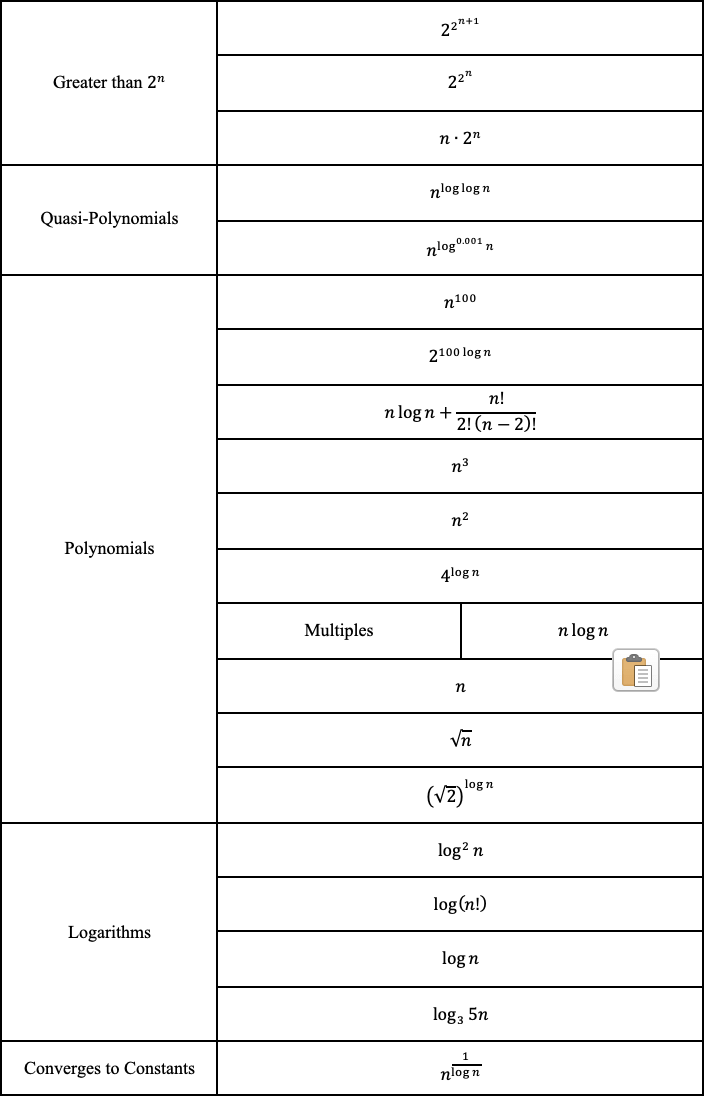
이해도를 테스트하기 위해 다음 함수들을 가장 복잡한 것부터 가장 간단한 것으로 순위를 매겨보세요. 해설과 함께 정답은 나중 섹션에서 찾을 수 있습니다. 이 중 일부는 까다롭기 때문에 좀 더 깊은 수학적 이해가 필요할 수 있습니다. 해설을 보면서 이해를 높이시길 바랍니다.

질문: 다음 함수들을 복잡도가 가장 높은 것부터 가장 낮은 것까지 나열하세요.

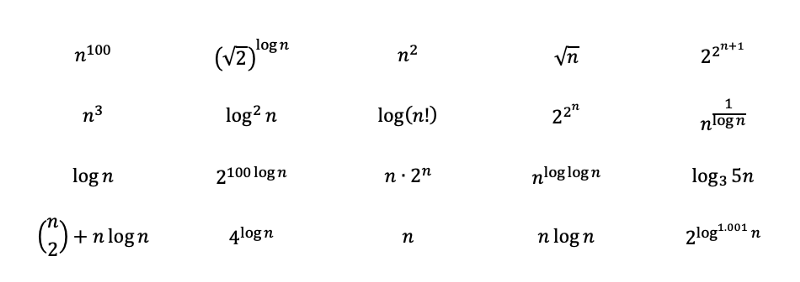교과서에 나온 연습문제에서 가져온 예시

섹션 2의 문제에 대한 해답:
이것은 실제로 당신의 이해도를 시험하기 위해 만든 트릭 문제였습니다. 중첩된 for 루프가 있어서 O(n²)로 답하게 만들려는 의도였습니다. 그러나 n은 입력 크기를 나타내는 것이어야 합니다. 이미지 배열이 입력이며, 각 픽셀이 한 번씩만 반복되었기 때문에 정답은 사실 O(n)입니다. 다음 섹션에서는 이와 같은 더 많은 예시를 다룰 것입니다.

5. 시간 및 공간 복잡도

지금까지는 알고리즘의 시간 복잡도에 대해서만 논의해왔습니다. 즉, 프로그램이 작업을 완료하는 데 걸리는 시간만 중요하게 여겼습니다. 하지만 프로그램이 작업을 완료하는 데 사용하는 메모리 크기도 중요합니다. 공간 복잡도는 프로그램이 사용할 메모리의 크기와 관련이 있으므로 분석해야 할 중요한 요소입니다.

공간 복잡도는 시간 복잡도와 비슷하게 작동합니다. 예를 들어, 선택 정렬의 공간 복잡도는 O(1)입니다. 이는 비교를 위해 하나의 최소값과 그 인덱스만 저장하기 때문에, 최대 사용 공간이 입력 크기와 함께 증가하지 않기 때문입니다.

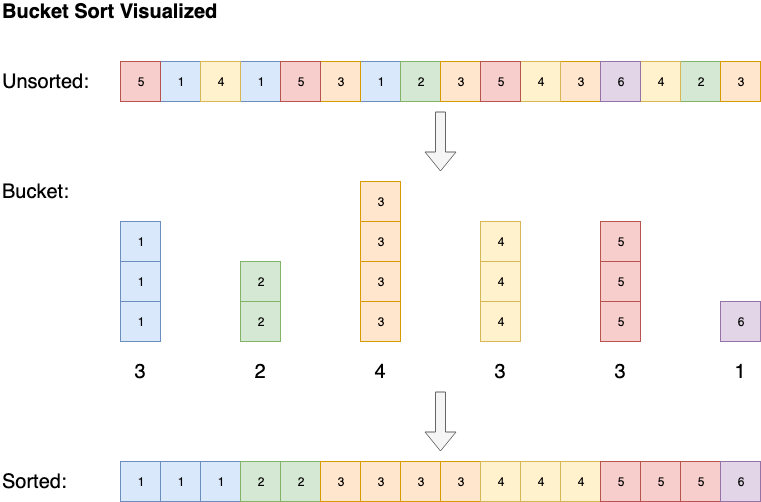
버킷 정렬과 같은 일부 알고리즘은 공간 복잡도는 O(n)이지만 시간 복잡도는 O(1)로 줄일 수 있습니다. 버킷 정렬은 배열의 모든 가능한 요소를 정렬 된 목록으로 만든 다음, 요소가 발견될 때마다 카운트를 증가시켜 배열을 정렬합니다. 마지막에 이 정렬된 배열은 요소의 카운트에 따라 반복된 정렬된 목록이 됩니다.

버킷 정렬 시각화

6. 최선, 평균, 최악, 예상 복잡도

복잡도는 최선의 경우, 최악의 경우, 평균적인 경우, 예상되는 경우로 분석될 수도 있습니다.

예를 들어 삽입 정렬을 살펴보면, 삽입 정렬은 리스트의 모든 요소를 반복해서 확인합니다. 요소가 이전 요소보다 작다면, 이전 요소보다 크기 전까지 요소를 뒤로 삽입합니다.

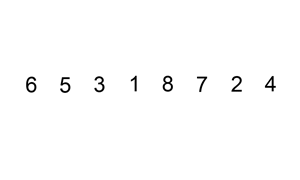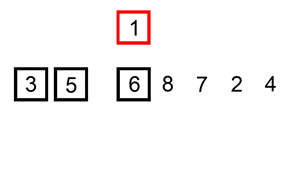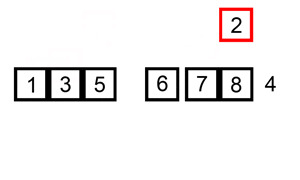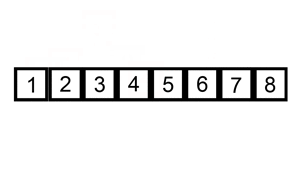삽입 정렬 시각화, 이미지 출처는 위키피디아

만약 배열이 초기에 정렬되어 있다면 교환 작업이 발생하지 않습니다. 알고리즘은 배열을 한 번만 반복하며, 이는 O(n)의 시간 복잡도를 결과로 낳습니다. 따라서 삽입 정렬의 최선의 경우 시간 복잡도는 O(n)입니다. O(n)의 복잡도는 종종 선형 복잡도라고도 합니다.

어떤 알고리즘은 운이 나쁠 때가 있습니다. 예를 들어, 퀵 정렬은 원소들이 역순으로 정렬된 경우 O(n) 시간이 걸릴 수 있지만, 평균적으로는 O(n * log(n)) 시간에 배열을 정렬합니다. 일반적으로 알고리즘의 시간 복잡도를 평가할 때는 최악의 경우 성능을 고려합니다. 이에 대해서는 다음 섹션에서 더 자세히 설명하겠습니다. 퀵 정렬에 대해서도 다음 섹션에서 자세히 다룰 것입니다.

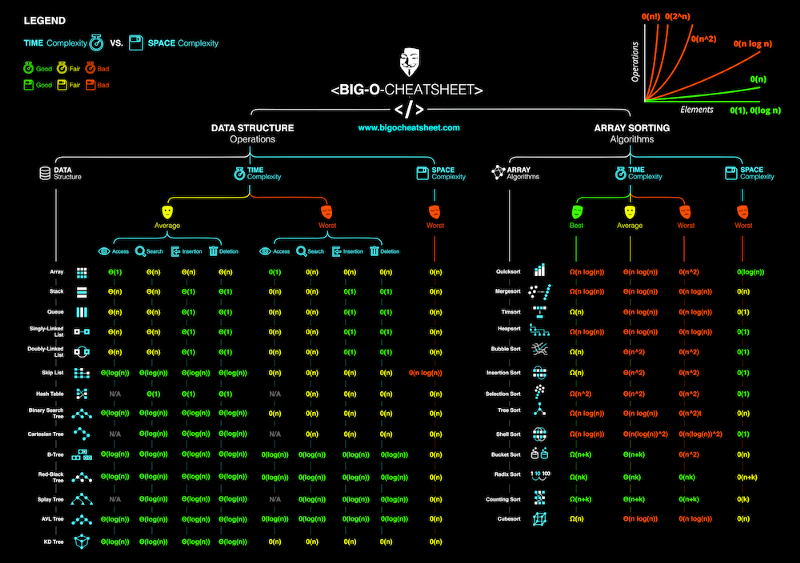
평균 복잡도는 알고리즘의 예상 성능을 설명합니다. 때때로 각 시나리오의 확률을 계산하는 것이 포함됩니다. 이러한 세부 정보를 설명하는 것은 꽤 복잡해 질 수 있기 때문에 이 글에서는 다루지 않겠습니다. 아래는 전형적인 알고리즘의 시간 및 공간 복잡도에 대한 치트 시트입니다.

공통 알고리즘에 대한 빅 오 치트시트

섹션 4의 문제에 대한 해답:
다음 다항식들을 규칙 3에 따라 즉시 가장 복잡한 것부터 가장 간단한 것까지 순위를 매겨야 합니다. 여기서 n의 제곱근은 단순히 n의 0.5 제곱입니다.

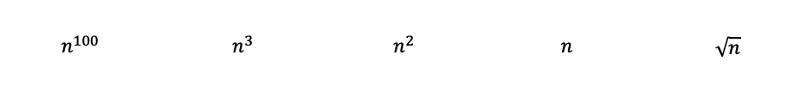
그러면 규칙 2와 규칙 6을 적용하여 다음과 같은 결과를 얻을 수 있습니다. 밑이 3인 로그함수는 로그 기본 변환으로 밑이 2인 로그함수로 변환될 수 있습니다. 밑이 3인 로그함수는 여전히 밑이 2인 로그함수보다 조금 더 느리게 증가하므로 그 다음 순위가 됩니다.

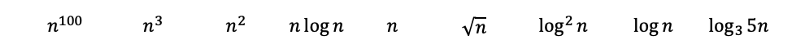
나머지 함수들은 조금 까다로워 보이지만, 그들의 진면목을 밝혀보고 어디에 위치시킬 수 있는지 살펴보겠습니다.

우선, 2의 2의 n제곱은 2의 n제곱보다 큽니다. 그리고 +1이 더해져 더욱 빨리 증가합니다.

그리고 2의 log₂n제곱(2^(log₂n))은 n 값과 같아진다는 사실을 이용하여 다음과 같이 변환할 수 있습니다. 0.001을 지수로 하는 로그는 상수보다 조금 더 빨리 증가하지만, 다른 거의 모든 것보다는 적게 증가합니다.

처음에 나온 식인 n^(log(logn))는 사실 상호-다항식(quasi-polynomial)의 변형으로, 다항식보다는 느리지만 지수함수보다는 빠릅니다. log(n)이 n보다 느리게 증가하기 때문에 그 복잡도는 조금 더 낮습니다. 역로그(inverse log)를 사용한 것은 1/log(n)이 무한대로 발산하기 때문에 상수에 수렴합니다.

팩토리얼은 곱셈으로 표현될 수 있기 때문에, 로그 함수 외부에서 덧셈으로 변환할 수 있습니다. _nC₂는 가장 큰 항이 3차항인 다항식으로 변환할 수 있습니다.

마지막으로, 우리는 이제 함수들을 가장 복잡한 것부터 가장 적은 복잡도를 가진 것까지 순위를 매길 수 있습니다.

빅오(Big-O)가 상관 없는 이유

!!! — 경고 — !!!

이 글에서 다루는 내용은 일반적으로 세계 대부분의 프로그래머들이 수용하지 않는 내용입니다. 이 내용을 논의하려면 스스로 책임을 지고 결정하셔야 합니다. 실제로 이런 내용을 이야기해서 구글 면접에 실패한 사람들이 블로그에 기록해 놓은 경우도 있습니다.

!!! — 경고 — !!!
이전에 우리는 퀵 정렬(quick sort)의 최악의 경우 시간 복잡도가 O(n²)이지만 병합 정렬(merge sort)의 경우 O(n * log(n))이라는 것을 배웠습니다. 그렇다면 병합 정렬이 더 빠를 것이라고 생각할 수 있습니다. 하지만 아마도 답이 거짓이라는 것을 이미 짐작하셨을 것입니다. 알고리즘은 그냥 퀵 정렬이 "빠른 정렬"이 되도록 연결되어 있습니다.

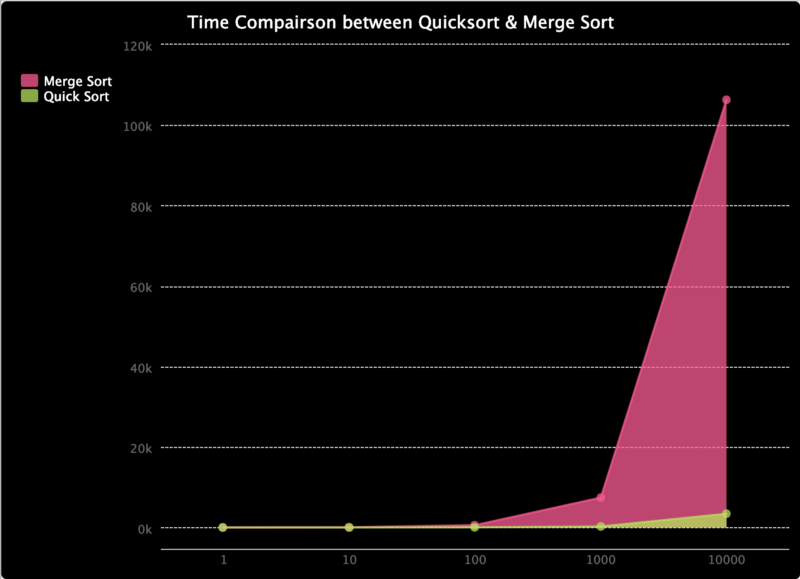
다음은 trinket.io를 사용해 만든 것으로, 퀵 정렬과 병합 정렬의 실행 시간을 비교합니다. 10000개 이하의 길이를 가진 배열에서만 테스트를 수행했지만, 그 범위 내에서 확인할 수 있는 바로는, 병합 정렬의 실행 시간이 퀵 정렬보다 더 빠르게 증가합니다. 퀵 정렬의 최악의 경우 시간 복잡도는 O(n²)이지만, 이 경우가 나타날 확률은 극히 낮습니다. 즉, O(n * log(n)) 복잡도에 따른 속도 증가를 비교할 때, 퀵 정렬은 평균적으로 더 나은 성능을 보입니다.

퀵 정렬과 병합 정렬의 시간 비교

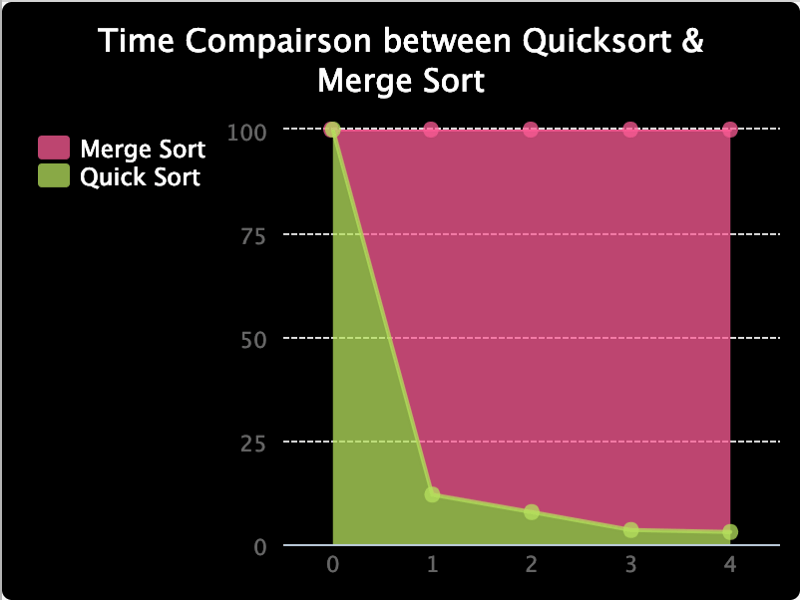
아래 그래프를 만들어서 두 정렬 방법의 소요 시간 비율을 비교해 보았습니다. 소요 시간이 낮은 값에서는 구별하기 어려웠기 때문입니다. 그래프에서 확인할 수 있듯, 퀵 정렬의 소요 시간 비율이 내림차순으로 나타납니다.

퀵 정렬과 병합 정렬의 시간 비율

이야기의 결론은, 빅 오 표기법은 알고리즘이 사용하는 리소스에 대한 참조를 제공하기 위한 수학적 분석일 뿐이라는 것입니다. 실제로 결과는 다를 수 있습니다. 그러나 알고리즘의 복잡도를 최대한 줄이는 것은 일반적으로 좋은 실천 방법이며, 알고리즘이 무엇을 하는지 정확하게 알고 있는 경우를 제외하고는 그렇게 하는 것이 좋습니다.

결론

저는 코딩을 좋아하며 새로운 것을 배우고 커뮤니티와 공유하는 것을 좋아합니다. 만약 특정한 분야에 흥미가 있다면 알려주세요. 보통 웹 디자인, 소프트웨어 아키텍처, 수학, 데이터 과학 등의 주제로 글을 쓰고 있습니다. 위의 주제 중 관심 있는 것이 있다면 제가 쓴 훌륭한 글을 찾아볼 수 있습니다.

컴퓨터 과학을 배우는 데 즐거운 시간 보내시길 바랍니다!!!