In this article, I will implement 8 graph algorithms that explore the search and combinatorial problems (traversals, shortest path and matching) of graphs in JavaScript.
The problems are borrowed from the book, Elements of Programming Interviews in Java. The solutions in the book are coded in Java, Python or C++ depending on what version of the book you own.
Although the logic behind the modeling of the problems is language-agnostic, the code snippets I provide in this article use some JavaScript caveats.
Every solution to each problem is broken down into 3 sections: an overview of the solution, the pseudocode, and lastly the actual code in JavaScript.
To test the code and see it do what it is supposed to do, you can use Chrome’s Dev Tools to run the snippets on the browser itself or use NodeJS to run them from the command line.
Graph implementation
The 2 most commonly used representations of graphs are the adjacency list and adjacency matrix.
The problems I’ll be solving are for sparse graphs (few edges), and the vertex operations in the adjacency list approach take constant (adding a vertex, O(1)) and linear time (deleting a vertex, O(V+E)). So I’ll stick with that implementation for the most part.
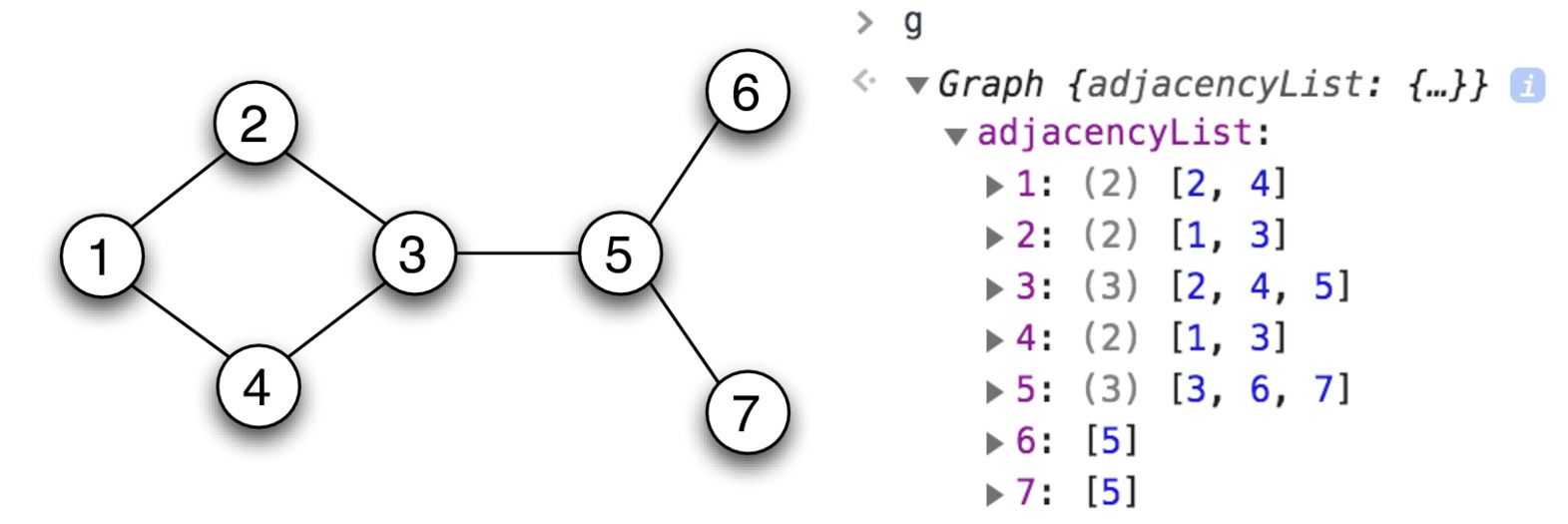
Let’s knock this out with a simple undirected, unweighted graph implementation using adjacency list. We’ll maintain an object (adjacencyList) that will contain all the vertices in our graph as the keys. The values will be an array of all the adjacent vertices. In the example below, vertex 1 is connected to vertices 2 and 4, hence adjacencyList: { 1 : [ 2, 4 ] } and so on for the other vertices.
To build the graph, we have two functions: addVertex and addEdge. addVertex is used to add a vertex to the list. addEdge is used to connect the vertices by adding the neighboring vertices to both the source and destination arrays since this is an undirected graph. To make a directed graph, we can simply remove lines 14–16 and 18 in the code below.
Before removing a vertex, we need to iterate through the array of neighboring vertices and remove all possible connections to that vertex.
class Graph {
constructor() {
this.adjacencyList = {};
}
addVertex(vertex) {
if (!this.adjacencyList[vertex]) {
this.adjacencyList[vertex] = [];
}
}
addEdge(source, destination) {
if (!this.adjacencyList[source]) {
this.addVertex(source);
}
if (!this.adjacencyList[destination]) {
this.addVertex(destination);
}
this.adjacencyList[source].push(destination);
this.adjacencyList[destination].push(source);
}
removeEdge(source, destination) {
this.adjacencyList[source] = this.adjacencyList[source].filter(vertex => vertex !== destination);
this.adjacencyList[destination] = this.adjacencyList[destination].filter(vertex => vertex !== source);
}
removeVertex(vertex) {
while (this.adjacencyList[vertex]) {
const adjacentVertex = this.adjacencyList[vertex].pop();
this.removeEdge(vertex, adjacentVertex);
}
delete this.adjacencyList[vertex];
}
}Graph traversals
Building on our implementation of graphs in the previous section, we’ll implement the graph traversals: breadth first search and depth first search.
Breadth First Search
BFS visits the nodes one level at a time. To prevent visiting the same node more than once, we’ll maintain a visited object.
Since we need to process the nodes in a First In First Out fashion, a queue is a good contender for the data structure to use. The time complexity is O(V+E).
function BFS
Initialize an empty queue, empty 'result' array & a 'visited' map
Add the starting vertex to the queue & visited map
While Queue is not empty:
- Dequeue and store current vertex
- Push current vertex to result array
- Iterate through current vertex's adjacency list:
- For each adjacent vertex, if vertex is unvisited:
- Add vertex to visited map
- Enqueue vertex
Return result arrayDepth First Search
DFS visits the nodes depth wise. Since we need to process the nodes in a Last In First Out manner, we’ll use a stack.
Starting from a vertex, we’ll push the neighboring vertices to our stack. Whenever a vertex is popped, it is marked visited in our visited object. Its neighboring vertices are pushed to the stack. Since we are always popping a new adjacent vertex, our algorithm will always explore a new level.
We can also use the intrinsic stack calls to implement DFS recursively. The logic is the same.
The time complexity is the same as BFS, O(V+E).
function DFS
Initialize an empty stack, empty 'result' array & a 'visited' map
Add the starting vertex to the stack & visited map
While Stack is not empty:
- Pop and store current vertex
- Push current vertex to result array
- Iterate through current vertex's adjacency list:
- For each adjacent vertex, if vertex is unvisited:
- Add vertex to visited map
- Push vertex to stack
Return result arrayGraph.prototype.bfs = function(start) {
const queue = [start];
const result = [];
const visited = {};
visited[start] = true;
let currentVertex;
while (queue.length) {
currentVertex = queue.shift();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
});
}
return result;
}
Graph.prototype.dfsRecursive = function(start) {
const result = [];
const visited = {};
const adjacencyList = this.adjacencyList;
(function dfs(vertex){
if (!vertex) return null;
visited[vertex] = true;
result.push(vertex);
adjacencyList[vertex].forEach(neighbor => {
if (!visited[neighbor]) {
return dfs(neighbor);
}
})
})(start);
return result;
}
Graph.prototype.dfsIterative = function(start) {
const result = [];
const stack = [start];
const visited = {};
visited[start] = true;
let currentVertex;
while (stack.length) {
currentVertex = stack.pop();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if (!visited[neighbor]) {
visited[neighbor] = true;
stack.push(neighbor);
}
});
}
return result;
}Search Maze
Problem Statement:
Given a 2D array of black and white entries representing a maze with designated entrance and exit points, find a path from the entrance to the exit, if one exists. – Aziz, Adnan, et al. Elements of Programming Interviews
We’ll represent the white entries with 0’s and black entries with 1’s. The white entries represent open areas and the black entries walls. The entrance and the exit points are represented by an array, the 0th index and the 1st index filled with the row and column indices, respectively.
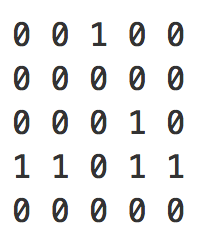
Solution:
- To move to a different position, we’ll hardcode the four possible movements in the directions array (right, bottom, left and top; no diagonal moves):
[ [0,1], [1,0], [0,-1], [-1,0] ]- To keep track of the cells we have already visited, we will replace the white entries (0’s) with black entries (1's). We are basically using DFS recursively to traverse the maze. The base case, that will end the recursion, is either we have reached our exit point and return true or we have visited every white entry and return false.
- Another important thing to keep track of is to ensure that we are within the boundaries of the maze all the time and that we only proceed if we are at a white entry. The isFeasible function will take care of that.
- Time Complexity: O(V+E)
Pseudocode:
function hasPath
Start at the entry point
While exit point has not been reached
1. Move to the top cell
2. Check if position is feasible (white cell & within boundary)
3. Mark cell as visited (turn it into a black cell)
4. Repeat steps 1-3 for the other 3 directionsvar hasPath = function(maze, start, destination) {
maze[start[0]][start[1]] = 1;
return searchMazeHelper(maze, start, destination);
};
function searchMazeHelper(maze, current, end) { // dfs
if (current[0] == end[0] && current[1] == end[1]) {
return true;
}
let neighborIndices, neighbor;
// Indices: 0->top,1->right, 2->bottom, 3->left
let directions = [ [0,1] , [1,0] , [0,-1] , [-1,0] ];
for (const direction of directions) {
neighborIndices = [current[0]+direction[0], current[1]+direction[1]];
if (isFeasible(maze, neighborIndices)) {
maze[neighborIndices[0]][neighborIndices[1]] = 1;
if (searchMazeHelper(maze, neighborIndices, end)) {
return true;
}
}
}
return false;
}
function isFeasible(maze, indices) {
let x = indices[0], y = indices[1];
return x >= 0 && x < maze.length && y >= 0 && y < maze[x].length && maze[x][y] === 0;
}
var maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]]
hasPath(maze, [0,4], [3,2]);Paint a Boolean Matrix
Problem Statement:
Implement a routine that takes an n X m Boolean array A together with an entry (x, y) and flips the color of the region associated with (x, y). – Aziz, Adnan, et al. Elements of Programming Interviews
The 2 colors will be represented by 0’s and 1’s.
In the example below, we start in the center of the array ([1,1]). Note that from that position, we can only reach the upper, leftmost triangular matrix. The rightmost, lowest position cannot be reached ([2,2]). Hence, at the end of the process, it’s the only color that is not flipped.

Solution:
- Like in the previous question, we will code an array to define the 4 possible moves.
- We’ll use BFS to traverse the graph.
- We’ll modify the isFeasible function slightly. It will still check if the new position is within the boundaries of the matrix. The other requirement is that the new position is colored the same as the previous position. If the new position fits the requirements, its color is flipped.
- Time complexity: O(mn)
Pseudocode:
function flipColor
Start at the passed coordinates and store the color
Initialize queue
Add starting position to queue
While Queue is not empty:
- Dequeue and store current position
- Move to the top cell
1. Check if cell is feasible
2. If feasible,
- Flip color
- Enqueue cell
3. Repeat steps 1-2 for the other 3 directionsfunction flipColor(image, x, y) {
let directions = [ [0,1] , [1,0] , [0,-1] , [-1,0] ];
let color = image[x][y];
let queue = [];
image[x][y] = Number(!color);
queue.push([x,y]);
let currentPosition, neighbor;
while (queue.length) {
currentPosition = queue.shift();
for (const direction of directions) {
neighbor = [currentPosition[0]+direction[0], currentPosition[1]+direction[1]];
if (isFeasible(image, neighbor, color)) {
image[neighbor[0]][neighbor[1]] = Number(!color);
queue.push([neighbor[0], neighbor[1]]);
}
}
}
return image;
}
function isFeasible(image, indices, color) {
let x = indices[0], y = indices[1];
return x >= 0 && x < image.length && y >= 0 && y < image[x].length && image[x][y] == color;
}
var image = [[1,1,1],[1,1,0],[1,0,1]];
flipColor(image,1,1);Compute Enclosed Regions
Problem Statement:
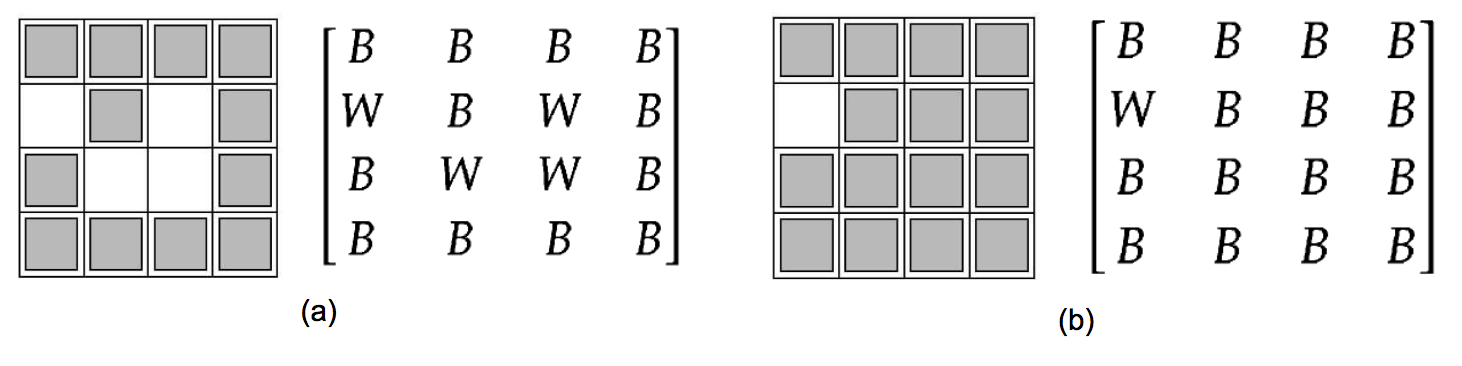
Let A be a 2D array whose entries are either W or B. Write a program that takes A, and replaces all Ws that cannot reach the boundary with a B. – Aziz, Adnan, et al. Elements of Programming Interviews
Solution:
- Instead of iterating through all the entries to find the enclosed W entries, it is more optimal to start with the boundary W entries, traverse the graph and mark the connected W entries. These marked entries are guaranteed to be not enclosed since they are connected to a W entry on the border of the board. This preprocessing is basically the complement of what the program has to achieve.
- Then, A is iterated through again and the unmarked W entries (which will be the enclosed ones) are changed into the B entries.
- We’ll keep track of the marked and unmarked W entries using a Boolean array of the same dimensions as A. A marked entry will be set to true.
- Time complexity: O(mn)
Pseudocode:
function fillSurroundedRegions
1. Initialize a 'visited' array of same length as the input array
pre-filled with 'false' values
2. Start at the boundary entries
3. If the boundary entry is a W entry and unmarked:
Call markBoundaryRegion function
4. Iterate through A and change the unvisited W entry to B
function markBoundaryRegion
Start with a boundary W entry
Traverse the grid using BFS
Mark the feasible entries as truefunction fillSurroundedRegions(board) {
if (!board.length) {
return;
}
const numRows = board.length, numCols = board[0].length;
let visited = [];
for (let i=0; i<numRows; i++) {
visited.push(new Array(numCols).fill(false, 0, numCols));
}
for (let i=0; i<board.length; i++) {
if (board[i][0] == 'W' && !visited[i][0]) {
markBoundaryRegion(i, 0, board, visited);
}
if (board[i][board.length-1] == 'W' && !visited[i][board.length-1]) {
markBoundaryRegion(i, board.length-1, board, visited);
}
}
for (let j=0; j<board[0].length; j++) {
if (board[0][j] == 'W' && !visited[0][j]) {
markBoundaryRegion(0, j, board, visited);
}
if (board[board.length-1][j] == 'W' && !visited[board.length-1][j]) {
markBoundaryRegion(board.length-1, j, board, visited);
}
}
for (let i=1; i<board.length-1; i++) {
for (let j=1; j<board.length-1; j++) {
if (board[i][j] == 'W' && !visited[i][j]) {
board[i][j] = 'B';
}
}
}
return board;
}
function markBoundaryRegion(i, j, board, visited) {
let directions = [ [0,1] , [1,0] , [0,-1] , [-1,0] ];
const queue = [];
queue.push([i,j]);
visited[i][j] = true;
let currentPosition, neighbor;
while (queue.length) {
currentPosition = queue.shift();
for (const direction of directions) {
neighbor = [i+direction[0], j+direction[1]];
if (isFeasible(board,visited,neighbor)) {
visited[neighbor[0]][neighbor[1]] = true;
queue.push(neighbor);
}
}
}
}
function isFeasible(board, visited, neighbor) {
let x = neighbor[0], y = neighbor[1];
return x >= 0 && x < board.length && y >= 0 && y < board[x].length && board[x][y] == 'W';
}
var board = [['B','B','B','B'],['W','B','W','B'],['B','W','W','B'],['B','B','B','B']];
fillSurroundedRegions(board);Deadlock Detection (Cycle In Directed Graph)
Problem Statement:
One deadlock detection algorithm makes use of a “wait-for” graph to track which other processes a process is currently blocking on. In a wait-for graph, processes are represented as nodes, and an edge from process P to 0 implies 0 is holding a resource that P needs and thus P is waiting for 0 to release its lock on that resource. A cycle in this graph implies the possibility of a deadlock. This motivates the following problem.
Write a program that takes as input a directed graph and checks if the graph contains a cycle. – Aziz, Adnan, et al. Elements of Programming Interviews
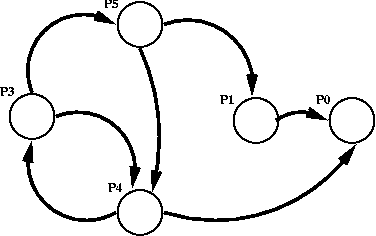
In the wait-for graph above, our deadlock detection program will detect at least one cycle and return true.
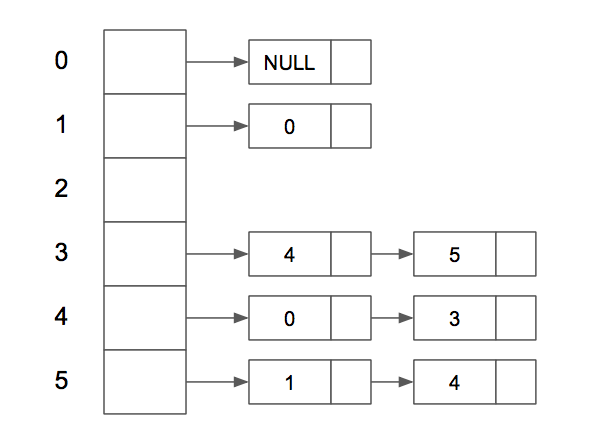
For this algorithm, we’ll use a slightly different implementation of the directed graph to explore other data structures. We are still implementing it using the adjacency list but instead of an object (map), we’ll store the vertices in an array.
The processes will be modeled as vertices starting with the 0th process. The dependency between the processes will be modeled as edges between the vertices. The edges (adjacent vertices) will be stored in a Linked List, in turn stored at the index that corresponds to the process number.
class Node {
constructor(data) {
this.data = data;
this.next = null;
}
}
class LinkedList {
constructor() {
this.head = null;
}
insertAtHead(data) {
let temp = new Node(data);
temp.next = this.head;
this.head = temp;
return this;
}
getHead() {
return this.head;
}
}
class Graph {
constructor(vertices) {
this.vertices = vertices;
this.list = [];
for (let i=0; i<vertices; i++) {
let temp = new LinkedList();
this.list.push(temp);
}
}
addEdge(source, destination) {
if (source < this.vertices && destination < this.vertices) {
this.list[source].insertAtHead(destination);
}
return this;
}
}
Solution:
- Every vertex will be assigned 3 different colors: white, gray and black. Initially all vertices will be colored white. When a vertex is being processed, it will be colored gray and after processing black.
- Use Depth First Search to traverse the graph.
- If there is an edge from a gray vertex to another gray vertex, we’ve discovered a back edge (a self-loop or an edge that connects to one of its ancestors), hence a cycle is detected.
- Time Complexity: O(V+E)
Pseudocode:
function isDeadlocked
Color all vertices white
Run DFS on the vertices
1. Mark current node Gray
2. If adjacent vertex is Gray, return true
3. Mark current node Black
Return falseconst Colors = {
WHITE: 'white',
GRAY: 'gray',
BLACK: 'black'
}
Object.freeze(Colors);
function isDeadlocked(g) {
let color = [];
for (let i=0; i<g.vertices; i++) {
color[i] = Colors.WHITE;
}
for (let i=0; i<g.vertices; i++) {
if (color[i] == Colors.WHITE) {
if (detectCycle(g, i, color)) {
return true;
}
}
}
return false;
};
function detectCycle(g, currentVertex, color) {
color[currentVertex] = Colors.GRAY;
let neighbor;
let nextNode = g.list[currentVertex].getHead();
while (nextNode !== null) {
neighbor = nextNode.data;
if (color[neighbor] == Colors.GRAY) {
return true;
}
if (color[neighbor] == Colors.WHITE && detectCycle(g, neighbor, color)) {
return true;
}
}
color[currentVertex] = Colors.BLACK;
return false;
}
let g = new Graph(3);
g.addEdge(0,1);
g.addEdge(0,2);
isDeadlocked(g);Clone Graph
Problem Statement:
Consider a vertex type for a directed graph in which there are two fields: an integer label and a list of references to other vertices. Design an algorithm that takes a reference to a vertex u, and creates a copy of the graph on the vertices reachable from u. Return the copy of u. – Aziz, Adnan, et al. Elements of Programming Interviews
Solution:
- Maintain a map that maps the original vertex to its counterpart. Copy over the edges.
- Use BFS to visit the adjacent vertices (edges).
- Time Complexity: O(n), where n is the total number of nodes.
Pseudocode:
function cloneGraph
Initialize an empty map
Run BFS
Add original vertex as key and clone as value to map
Copy over edges if vertices exist in map
Return cloneclass GraphVertex {
constructor(value) {
this.value = value;
this.edges = [];
}
}
function cloneGraph(g) {
if (g == null) {
return null;
}
let vertexMap = {};
let queue = [g];
vertexMap[g] = new GraphVertex(g.value);
while (queue.length) {
let currentVertex = queue.shift();
currentVertex.edges.forEach(v => {
if (!vertexMap[v]) {
vertexMap[v] = new GraphVertex(v.value);
queue.push(v);
}
vertexMap[currentVertex].edges.push(vertexMap[v]);
});
}
return vertexMap[g];
}
let n1 = new GraphVertex(1);
let n2 = new GraphVertex(2);
let n3 = new GraphVertex(3);
let n4 = new GraphVertex(4);
n1.edges.push(n2, n4);
n2.edges.push(n1, n3);
n3.edges.push(n2, n4);
n4.edges.push(n1, n3);
cloneGraph(n1);Making Wired Connections
Problem Statement:
Design an algorithm that takes a set of pins and a set of wires connecting pairs of pins, and determines if it is possible to place some pins on the left half of a PCB, and the remainder on the right half, such that each wire is between left and right halves. Return such a division, if one exists. – Aziz, Adnan, et al. Elements of Programming Interviews
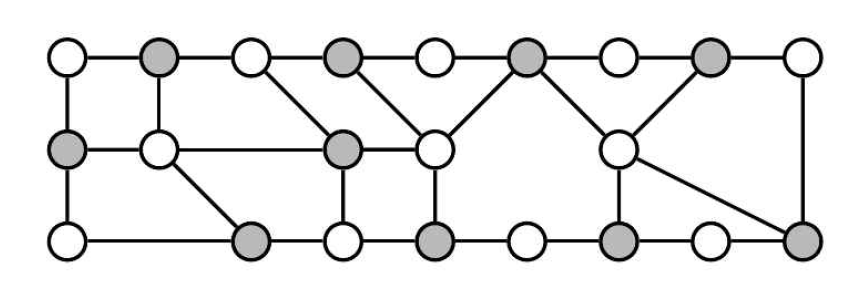
Solution:
- Model the set as a graph. The pins are represented by the vertices and the wires connecting them are the edges. We’ll implement the graph using an edge list.
The pairing described in the problem statement is possible only if the vertices (pins) can be divided into “2 independent sets, U and V such that every edge (u,v) either connects a vertex from U to V or a vertex from V to U.” (Source) Such a graph is known as a Bipartite graph.
To check whether the graph is bipartite, we’ll use the graph coloring technique. Since we need two sets of pins, we have to check if the graph is 2-colorable (which we’ll represent as 0 and 1).
Initially, all vertices are uncolored (-1). If adjacent vertices are assigned the same colors, then the graph is not bipartite. It is not possible to assign two colors alternately to a graph with an odd length cycle using 2 colors only, so we can greedily color the graph.
Extra step: We will handle the case of a graph that is not connected. The outer for loop takes care of that by iterating over all the vertices.
- Time Complexity: O(V+E)
Pseudocode:
function isBipartite
1. Initialize an array to store uncolored vertices
2. Iterate through all vertices one by one
3. Assign one color (0) to the source vertex
4. Use DFS to reach the adjacent vertices
5. Assign the neighbors a different color (1 - current color)
6. Repeat steps 3 to 5 as long as it satisfies the two-colored constraint
7. If a neighbor has the same color as the current vertex, break the loop and return falsefunction isBipartite(graph) {
let color = [];
for (let i=0; i<graph.length; i++) {
color[i] = -1;
}
for (let i=0; i<graph.length; i++) {
if (color[i] == -1) {
let stack = [];
stack.push(i);
color[i] = 0;
let node;
while (stack.length) {
node = stack.pop();
for (const neighbor of graph[node]) {
if (color[neighbor] == -1) {
stack.push(neighbor);
color[neighbor] = 1 - color[node];
}
else if (color[neighbor] == color[node]) {
return false;
}
}
}
}
}
return true;
}
isBipartite([[],[2,4,6],[1,4,8,9],[7,8],[1,2,8,9],[6,9],[1,5,7,8,9],[3,6,9],[2,3,4,6,9],[2,4,5,6,7,8]]);Transform one string to another
Problem Statement:
Given a dictionary D and two strings s and f, write a program to determine if s produces t. Assume that all characters are lowercase alphabets. If s does produce f, output the length of a shortest production sequence; otherwise, output -1. – Aziz, Adnan, et al. Elements of Programming Interviews
For example, if the dictionary D is ["hot", "dot", "dog", "lot", "log", "cog"], s is "hit" and t is "cog", the length of the shortest production sequence is 5.
"hit" -> "hot" -> "dot" -> "dog" -> "cog"
Solution:
- Represent the strings as vertices in an undirected, unweighted graph, with an edge between 2 vertices if the corresponding strings differ in one character at most. We'll implement a function (compareStrings) that calculates the difference in characters between two strings.
- Piggybacking off the previous example, the vertices in our graph will be
{hit, hot, dot, dog, lot, log, cog}- The edges represented by the adjacency list approach we discussed in section 0. Graph Implementation, will be:
{
"hit": ["hot"],
"hot": ["dot", "lot"],
"dot": ["hot", "dog", "lot"],
"dog": ["dot", "lot", "cog"],
"lot": ["hot", "dot", "log"],
"log": ["dog", "lot", "cog"],
"cog": ["dog", "log"]
}- Once we finish building the graph, the problem boils down to finding the shortest path from a start node to a finish node. This can be naturally computed using Breadth First Search.
- Time Complexity: O(M x M x N), where M is the length of each word and N is the total number of words in the dictionary.
Pseudocode:
function compareStrings
Compare two strings char by char
Return how many chars differ
function transformString
1. Build graph using compareStrings function. Add edges if and only if the two strings differ by 1 character
2. Run BFS and increment length
3. Return length of production sequencefunction transformString(beginWord, endWord, wordList) {
let graph = buildGraph(wordList, beginWord);
if (!graph.has(endWord)) return 0;
let queue = [beginWord];
let visited = {};
visited[beginWord] = true;
let count = 1;
while (queue.length) {
let size = queue.length;
for (let i=0; i<size; i++) {
let currentWord = queue.shift();
if (currentWord === endWord) {
return count;
}
graph.get(currentWord).forEach( neighbor => {
if (!visited[neighbor]) {
queue.push(neighbor);
visited[neighbor] = true;
}
})
}
count++;
}
return 0;
};
function compareStrings (str1, str2) {
let diff = 0;
for (let i=0; i<str1.length; i++) {
if (str1[i] !== str2[i]) diff++
}
return diff;
}
function buildGraph(wordList, beginWord) {
let graph = new Map();
wordList.forEach( (word) => {
graph.set(word, []);
wordList.forEach( (nextWord) => {
if (compareStrings(word, nextWord) == 1) {
graph.get(word).push(nextWord);
}
})
})
if (!graph.has(beginWord)) {
graph.set(beginWord, []);
wordList.forEach( (nextWord) => {
if (compareStrings(beginWord, nextWord) == 1) {
graph.get(beginWord).push(nextWord);
}
})
}
return graph;
}Where to go from here?
Hopefully, by the end of this article, you have realized that the most challenging part in graph problems is identifying how to model the problems as graphs. From there, you can use/modify the two graph traversals to get the expected output.
Other graph algorithms that are nice to have in your toolkit are:
- Topological Ordering
- Shortest Path Algorithms (Dijkstra and Floyd Warshall)
- Minimum Spanning Trees Algorithms (Prim and Kruskal)
If you found this article helpful, consider buying me a coffee. It will keep me awake when I work on a video tutorial of this article :)
References:
Aziz, Adnan, et al. Elements of Programming Interviews. 2nd ed., CreateSpace Independent Publishing Platform, 2012.