by Joe Chasinga
A functional approach to mergesort algorithm

Algorithms are often difficult for people to understand. I believe that this is because they are most often programmed or explained in a language that encourages thinking in procedures or instructions which are not intuitive.
Very often the meat of an algorithm (how you solve a particular problem logically without computer coding) looks very simple and understandable when described graphically. Surprisingly, however, it often does not translate well into code written in languages like Python, Java, or C++. Therefore it becomes much more difficult to understand.
In other words, the algorithmic concept doesn’t map directly to how the code should be written and read.
Why are algorithms so difficult to code?
Well, we could blame it on the inner workings of early electro-mechanic computers. The early inventors of some of the most used programming languages today could never get rid of those features. Or perhaps they couldn’t help leaving their fingerprints on their inventions. Once you understand computers that well, there’s no undoing that.
To make matters worse, on top of already micro-managing languages, somebody had to invent an API for better micro-management. They called it object-oriented programming (OOP), and added the concept of classes to programming — but I think modules and functions could handle the same things just fine, thank you very much.
C++ didn’t make C any better, but it did pave a way by inspiring more descendants of OOP. And all together, all these things make abstract algorithmic thinking hard for the aforementioned reasons.
The case study: merge sort
For our discussion, we will use a merge sort algorithm as a specimen. Take a look at the diagram below. If you can count and put together jigsaw puzzles, then you can probably understand how it works in a few minutes.
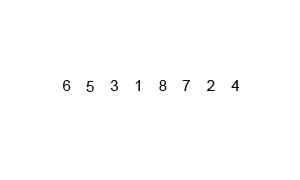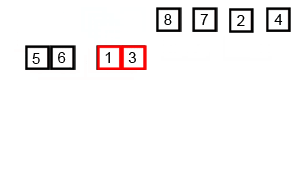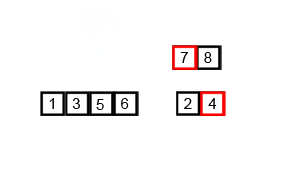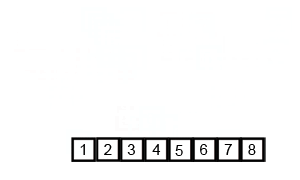
The key steps of producing a merge sort are few and simple. In fact, I can explain it using my daughter’s number blocks (helpful to follow these by going back to the animated diagram for reference):
- First, we need to keep subdividing a list of numbers (or letters, or any type of sortable values) by half until we end up with many single-element lists. A list with one element is technically sorted. This is called trivially sorted.
- Then, we create a new empty list in which we could start re-arranging the elements and putting them one by one according to which one is less/smaller than the other.
- Then we need to “merge” each pair of lists back together, effectively reversing the subdivision steps. But this time, at every step of the way, we have to make sure that the smaller element in the pair in question is being put into the empty list first.
For the sake of the argument, we will try to map out the above processes by making each one a subroutine (function in normal speak). The meatiest part of this algorithm is the merging, so let’s start with that first.
def merge(a, b):
out = []
while (len(a) > 0 and len(b) > 0):
if (a[0] <= b[0]):
out.append(a[0])
del a[0]
else:
out.append(b[0])
del b[0]
while (len(a) > 0):
out.append(a[0])
del a[0]
while (len(b) > 0):
out.append(b[0])
del b[0]
return outGo on and spend some time looking it over. You might notice that with imperative Python code, it is designed to be spoken out and then understood. It is very understandable in English, but not in logic.
Our first attempt
Here is one attempt (that you could possibly use in a whiteboarding session):
To merge list a and b, we’ll have to first create an empty list named out for clarity (because in Python we can’t be sure it will really be “out” in the end). Then, as long as (or while) both lists are not empty, we’ll keep putting the head of both lists to a fight-off. Whichever is less than or equal to the opponent wins and gets to enter out first. The loser will have to stay and wait there for the new contestant down the line. The rematches continue on until the first while loop breaks.
Now, at some point either a or b will be empty, leaving the other with one or more elements hanging. Without any contestants left in the other list, the two while loops make sure to fast track those poor elements into out so both list are exhausted. Then, when that’s all done, we return out.
And this is the test cases for merge:
assert(merge([1], [2]) == [1, 2])
assert(merge([2], [1]) == [1, 2])
assert(merge([4, 1], [3, 0, 2]) == [3, 0, 2, 4, 1])I hope at this point it is clear to you why we end up with the result in the last case. If it isn’t, try drawing on a whiteboard or a piece of paper and simulating the explanation.
Divide and Conquer
Now we will carry on with the subdivision part. This process is also known as partitioning or, in somewhat grander language, Divide and Conquer (by the way, the definition in politics is equally interesting).

Basically, if anything is hard to conquer or understand, you should break it down until it becomes smaller and more easily understood. Do that until the parts are unbreakable and repeat the process with the rest.
def half(arr):
mid = len(arr) / 2
return arr[:mid], arr[mid:]What the half routine does is find the middle index, slice the input list into roughly equal sublists, and return both as a pair. It only needs to do this once, since the parent function will eventually call it recursively.
Since we have the pieces, now we just need to put them together into a coherent scheme. This is where the water gets murky, because recursions are involved.
Before going into more code, let me explain why recursions and imperative programming languages like Python do not fit together so well. I won’t go into the topic of optimization, because that does not concern today’s discussion and is not as interesting.
One distinct irony here is that, even in a language with iterative looping like Python, it still cannot entirely avoid recursion (it might get away without recursion, but I’m sure that would make it even more bizarre). Recursion is a territory where iterative constructs, such as for and while loops, become utterly useless.
Moreover, recursion is not natural in Python. It does not feel natural and transparent, but rather feels quite half-baked the way its lambda is. An attempt at voicing over recursions in Python would be like, “then we do this recursively and just pray it all works out and hits the base case in the end so it doesn’t spiral into the infinite darkness of stack overflow.” Wow, right?
So here is the mergesort function:
def mergesort(arr):
if (len(arr) <= 1):
return arr
left, right = half(arr)
L = mergesort(left)
R = mergesort(right)
return merge(L, R)Apparently, this is really clean and easy to read. But it isn’t clear what happens after the call to half , at least semantically. Because of this “non-nativity” to recursion, recursive calls are very opaque and obstructive to educational endeavors.
The only way to visualize this mergesort process is probably to track the changes in the sublists in every step:
input: [0, 3, 1, 3, 2, 6, 5]
A alias for mergesort / half
B alias for merge
## subdividing by half ...
A([0, 3, 1, 3, 2, 6, 5])
A([0, 3, 1]) A([3, 2, 6, 5])
A([0]) A([3, 1]) A([3, 2]) A([6, 5])
A([]) A([0]) A([3]) A([1]) A([3]) A([2]) A([6]) A([5])
## base case reached, start merging ...
B([], [0]) B([3], [1]) B([3], [2]) B([6], [5])
B([0], [1, 3]) B([2, 3], [5, 6])
B([0, 1, 3], [2, 3, 5, 6])
B([0, 1, 2, 3, 3, 5, 6])
output: [0, 1, 2, 3, 3, 5, 6]On an asymptotic side note, dividing and conquering almost always incurs a logarithmic runtime. When you keep dividing a collection into N sub-collections, whether it contains 10 or 100,000,000 items, the number of steps taken in the latter case increases at the rate of log base N.
For instance, it takes about 3 steps to keep dividing 10 by 2 until it gets as close to 1 as it can (or exactly 3 steps to reach 1 in integer division). But it takes only about 26 steps to do the same and divide 100,000,000 by 2 until you reach 1. This fact can be expressed as follows:
2^3.321928 = 10
2^6.643856 = 100
...
2^26.575425 = 100000000
or
log base 2 of 100000000 = 26.575425The takeaway here is that we had to visualize the recursive processes in order to understand the inner workings of the algorithm — even though it looked so trivial in the animated diagram.
Why is there a divide between the conceptual processes of the algorithm itself and the code that instructs the computer to compute such processes?
It’s because in a way, by using imperative languages, we are in fact still mentally enslaved by the machines.

Diving deeper into the code
“There’s a difference between knowing the path and walking the path.”
― Morpheus, The Matrix
Programming is hard, we all know that. And understanding programming in a really deep way is even harder on your soul (and your career). But I would argue that, like Morpheus said, sometimes walking the path is all that matters. Being able to see clearly is one of most rewarding things in programming.
In functional programming, the programmer (you) gets the front seat in seeing how data change recursively. This means that you have the ability to decide how the data of a certain form should be transformed to the data of another based on the snapshot of how it looks. This isn’t unlike how we have visualized the mergesort process. Let me give you a preview.
Let’s say you want to create a base case in Python. In it, you want to return the list in question when it has only one element, and an empty list when there’s two elements. So you’d need to write something like this:
if (len(arr) == 1):
return arr
elif (len(arr) == 2):
return []Or to make this worse but more interesting, you could try to access the first element by index 0 and the second element by index 1 and get ready to handle IndexError exception.
In a functional language like Erlang — which is what I’ll be using in this article for its dynamic type system like Python — you more or less would do something like this:
case Arr of
[_] -> Arr;
[_,_] -> []
end.This gives you a clearer view of the state of the data. Once it’s trained enough, it requires much less cognitive power to read and comprehend what the code does than len(arr) . Just keep in mind: a programmer who doesn’t speak English might ask, “what is len?” Then you get distracted by the literal meaning of the function instead of the value of that expression.
However, this comes with a price: you don’t have the luxury of a looping construct. A language like Erlang is recursion-native. Almost every meaningful Erlang program will make use of rigorous recursive function calls. And that’s why it is mapped more closely to the algorithmic concepts which usually consist of recursion.
Let’s try to retrace our steps in producing mergesort, but this time in Erlang, starting with the merge function.
merge([], [], Acc) -> Acc;
merge([], [H | T], Acc) -> [H | merge([], T, Acc)];
merge([H | T], [], Acc) -> [H | merge(T, [], Acc)];
merge([Ha | Ta], [Hb | Tb], Acc) ->
case Ha =< Hb of
true -> [Ha | merge(Ta, [Hb | Tb], Acc)];
false -> [Hb | merge([Ha | Ta], Tb, Acc)]
end.What an abomination! Definitely not an improvement in terms of readability, you think. Yes, Erlang admittedly won’t win any prizes for beautiful language. In fact, many functional languages can look like gibberish to the untrained eyes.
But let’s give it a chance. We will go through each step like we did before, and perhaps in the end some of us will see the light. But before we go on, for those of you who are not familiar with Erlang, these are some points worth noting:
- Each block of
mergeis considered a function clause of the same function. They are separated by;. When an expression ends in Erlang, it ends with a period (.). It’s a convention to separate a function into several clauses for different cases. For instance,merge([], [], Acc) -> Acc; clause maps the case where the first two arguments are empty lists to the value of the last argument. - Arity plays an important role in Erlang. Two functions with the same name and arity are considered the same function. Otherwise, they aren’t. For example,
merge/1andmerge/3(how functions and their arity are addressed in Erlang) are two different functions. - Erlang uses rigorous pattern matching (This is used in many other functional languages, but especially in Erlang). Since values in pure functional languages are immutable, it is safe to bind variables in a similar shape of data to the existing one with a matched shape. Here is a trivial example:
{X, Y} = {0.5, 0.13}.
X. %% 0.5
Y. %% 0.13
[A, B, C | _] = [alice, jane, bob, kent, ollie].
[A, B, C]. %% [alice, jane, bob]- Note that we will seldom talk about returning values when we work with Erlang functions, because they don’t really “return” anything per se. It maps an input value to a new value. This isn’t the same as outputting or returning it from the function. The function application itself is the value. For instance, if
Add(N1, N2) -> N1+N2., Add(1,2) is 3. There’s no way for it to return anything other than 3, hence we can say it is 3. This is why you could easilydo add_one = add(1) and then add_one(2) is3, add_one(5) is 6, and so on.
For those who are interested, see referential transparency. To make this point clearer and risking redundancy, here is something to think about:
whenf(x)is a function with one arity, and the mapping isf(x) ->; x , then it's conclusive that f(1) -> 1, f(2)-> 2, f(3.1416)->3.1416, and f("foo") -> "foo".
This may look like a no-brainer, but in an impure function there's no such guaranteed mapping:a = 1def add_to_a(b):return b + a
Nowamight as well be anything beforeadd_to_agets called. Thus in Python, you could write a pure version of the above as:def add(a, b):return a + b
orlambda a, b: a + b.
Now it’s time to bumble into the unknown.

Forging ahead with Erlang
merge([], [], Acc) -> Acc;The first clause of the merge/3 function means that when the first two arguments are empty lists, map the entire expression to (or “return”) the third argument Acc.
Interestingly, in a pure function, there’s no way of retaining and mutating state outside of itself. We can only work with what we have received as inputs into the function, transform it, then feed the new state into another function’s argument (most often this is another recursive call to itself).
Here, Acc stands for accumulator, which you can think of as a state container. In the case of merge/3, Acc is a list that starts empty. But as the recursive calls get on, it accumulates values from the first two lists using the logic we program (which we will talk about next).
This process of exhausting a value to build up another value is collectively known as reduction. Therefore, in this case it we can conclude that since the first two lists are exhausted (empty), Acc must be ripe for pick up.
merge([], [H | T], Acc) -> [H | merge([], T, Acc)];The second clause matches the case when the first list is already empty, but there’s still at least one more element in the second list. [H | T] means a list has a head element H which cons onto another list T. In Erlang, a list is a linked list, and the head has a pointer to the rest of the list. So a list of [1, 2, 3, 4] can be thought of as:
%% match A, B, C, and D to 1, 2, 3, and 4, respectively
[A | [B | [C | [D | []]]]] = [1, 2, 3, 4].In this case, as you can see in the conning example, T can just be an empty tail list. So in this second case, we map it to a value of a new list in which the H element of the second list is conned onto the recursive result of calling merge/3 when T is the second argument.
merge([H | T], [], Acc) -> [H | merge(T, [], Acc)];The third case is just a flip side of the second case. It matches the case when the first list is not empty, but the second is. This clause maps to a value in a similar pattern, except it calls merge/3 with the tail of the first list as the first argument and keeps the second list empty.
merge([Ha | Ta], [Hb | Tb], Acc) ->
case Ha =< Hb of
true -> [Ha | merge(Ta, [Hb | Tb], Acc)];
false -> [Hb | merge([Ha | Ta], Tb, Acc)]
end.Let’s begin with the meat of merge/3 first. This clause matches the case when the first and second arguments are non-empty lists. In this case, we enter a case … of clause (equivalent to switch case in other languages) to test if the head element of the first list (Ha) is less than or equal to the head element of the second list (Hb).
If that is true, we con Ha onto the resulting list of the next recursive call to merge with the tail list of the previous first list (Ta) as the new first argument. We keep the second and third arguments the same.
These clauses constitute to a single function, merge/3. You can imagine that it could have been a single function clause. We could use complex case … of and/or if conditional plus pattern-matching to weed out each case and map it to the right result. That would have made it more chaotic, when you can easily read each case the function is matching quite nicely on separate lines.
However, things got a little hairy for the subdividing operation, which needs two functions: half/1 and half/3.
half([]) -> {[], []};
half([X]) -> {[X], []};
half([X,Y]) -> {[X], [Y]};
half(L) ->
Len = length(L),
half(L, {0, Len}, {[], []}).
half([], _, {Acc1, Acc2}) ->
{lists:reverse(Acc1), lists:reverse(Acc2)};
half([X], _, {Acc1, Acc2}) ->
{lists:reverse(Acc1), lists:reverse([X | Acc2])};
half([H|T], {Cnt, Len}, {Acc1, Acc2}) ->
case Cnt >= (Len div 2) of
true -> half(T, {Cnt + 1, Len}, {Acc1, [H|Acc2]});
false -> half(T, {Cnt + 1, Len}, {[H|Acc1], Acc2})
end.This is where you’ll miss Python and its destructive nature. In a pure functional language, lists are linked lists. When you work with them, there’s no looking back. There’s no logic that says “I want to divide a list in half, so I’m going to get the middle index, and slice it into two left and right portions.”
If your mind is set in working with linked lists, you’re more along the lines of “I can only go forward through the list, working with a few elements at a time. I need to create two empty lists and keep count of how many items I’ve retrieve from the source list and put into the first one so I know when it’s time to switch to another bucket. All the aforementioned needs to be passed in as arguments in the recursive calls.” Whew!
In other words, cutting a list in half can be compared to chopping a block of cheese with a knife in the middle of it. On the other hand, a functional comparison for doing so is like pouring coffee into two cups equally — you just need to know when it’s time to stop pouring into the first one and move on to the second one.
The half/1 function, although it isn’t really necessary, is there for convenience.
half([]) -> {[], []};
half([X]) -> {[X], []};
half([X,Y]) -> {[X], [Y]};
half(L) ->
Len = length(L),
half(L, {0, Len}, {[], []}).By now, you should get the sense of what each Erlang function clause is doing. The new bracket pairs here represent tuples in Erlang. Yes, we are returning a left and right value pair, like in the Python version. The half/1 function is here to handle simple, explicit base cases which don’t warrant the worthiness of passing in other arguments.
However, take note of the last case when the argument has a list with more than two elements. (Note: those with less than or equal to two elements are already handled by the first three clauses.) It simply computes the following:
- the length of the list
Land callshalf/3withLas the first argument - a pair of counter variables and list’s length, which will be used to signal the switching from list one to list two
- and of course, a pair of empty lists to fill the elements from
Lin.
half([], _, {Acc1, Acc2}) ->
{lists:reverse(Acc1), lists:reverse(Acc2)};half/3 looks like a mess, but only to the untrained eyes. The first clause matches a pattern when the source list is drained. In this case, the second pair of counter and length won’t matter since it’s already the end. We simply know that Acc1 and Acc2 are ripe for yielding. But wait, what’s with the reversing of both?
Appending an element to a linked list is a very slow operation. It runs O(N) times for every append, because it needs to create a new list, copy the existing one onto it, and create a pointer to the new element and assign it to the last element. It’s like redoing the whole list. Couple this with recursions and you are bound for disaster.
The only good way to add something to a linked list is to prepend it at the head. Then all it needs to do is create a memory for that new value and give it a reference to the head of the linked list. A simple O(1) operation. So even though we could concatenate lists using ++ like [1, 2, 3] ++ [4], we rarely want to do it this way, especially with recursions.
The technique here is to reverse the source list first, then con an element onto it like [4 | [3, 2, 1]] , and reverse them again to get the right result. This may sound terrible, but reversing a list and reversing it back is an O(2N) operation, which is O(N). But in between, conning elements onto the list takes only O(1), so it basically costs no extra runtime.
half([H|T], {Cnt, Len}, {Acc1, Acc2}) ->
case Cnt >= (Len div 2) of
true -> half(T, {Cnt + 1, Len}, {Acc1, [H|Acc2]});
false -> half(T, {Cnt + 1, Len}, {[H|Acc1], Acc2})
end.Getting back to half/3. The second clause, the meat of the function, does exactly the same thing as the coffee pouring metaphor we visited earlier. Since the source list is still “emitting” data, we want to keep track of the time we have been pouring values from it into the first coffee cup Acc1.
Remember that in half/1’s last clause, we calculated the length of the original list? That is the Len variable here, and it stays the same throughout all the calls. It’s there so that we can compare Cnt counter to it divided by 2 to see if we have come to the middle of the source list and should switch to filling up Acc2 . That is where the case … of comes in.
Now, let’s put them all together in mergesort/1 . This should be as simple as the Python version, and can be easily compared.
mergesort([A]) -> [A];
mergesort([A, B]) ->
case A =< B of
true -> [A,B];
false -> [B,A]
end;
mergesort(L) ->
{Left, Right} = half(L),
merge(mergesort(Left), mergesort(Right), []).That’s it!
At this point, either you think this is a novel and useful way of thinking about a problem, or you find it just plain confusing. But I hope you got something out of this programming approach that helps shine new light on how we can think about algorithms.
Update
The Python implementation of merge function isn’t efficient because in each while loop the first element in the list is removed. Although this is a common pattern in functional languages like Erlang, in Python it is very costly to remove or insert an element anywhere other than the last position because unlike a list in Erlang which is a linked list which is very efficient to remove or add element at the head of the list, Python list behaves like an array which has to reposition all other elements when one is removed or added, incurring a O(n) runtime.
The better way is to sacrifice little space to define a counter variable for each list which can be incremented and used to access the current element of the source list without the need to remove the top-most element at all.
def merge(a, b):
out = []
ai = 0
bi = 0
while (ai <= len(a) - 1 and bi <= len(b) - 1):
if (a[ai] <= b[bi]):
out.append(a[ai])
ai += 1
else:
out.append(b[bi])
bi += 1
while (ai <= len(a) - 1):
out.append(a[ai])
ai += 1
while (bi <= len(b) - 1):
out.append(b[bi])
bi += 1
return out