Machine learning is changing the world. Google uses machine learning to suggest search results to users. Netflix uses it to recommend movies for you to watch. Facebook uses machine learning to suggest people you may know.
Machine learning has never been more important. At the same time, understanding machine learning is hard. The field is full of jargon. And the number of different ML algorithms grows each year.
This article will introduce you to the fundamental concepts within the field of machine learning. More specifically, we will discuss the basic concepts behind the 9 most important machine learning algorithms today.
Recommendation Systems
What Are Recommendation Systems?
Recommendation systems are used to find similar entries in a data set.
Perhaps the most common real-world example of a recommendation exists inside of Netflix. More specifically, its video streaming service will recommend suggested movies and TV shows based on content that you’ve already watched.
Another recommendation system is Facebook’s “People You May Know” feature, which suggests possible friends for you based on your existing friends list.
Fully developed and deployed recommendation systems are extremely sophisticated. They are also very resource-intensive.
Recommendation Systems and Linear Algebra
Fully-fledged recommendation systems require a deep background in linear algebra to build from scratch.
Because of this, there might be concepts in this section that you do not understand if you’ve never studied linear algebra before.
Don’t worry, though – the scikit-learn Python library makes it very easy to build recommendation systems. S0 you don't need much of a linear algebra background to build real-world recommendation systems.
How Do Recommendation Systems Work?
There are two main types of recommendation systems:
- Content-based recommendation systems
- Collaborative filtering recommendation systems
Content-based recommendation systems give you recommendations based on items’ similarity of items that you’ve already used. They behave exactly how you’d expect a recommendation system to behave.
Collaborative filtering recommendation systems produce recommendations based on knowledge of the user’s interactions with items. Said differently, they use the wisdom of the crowds. (Hence the term “collaborative” in its name.)
In the real world, collaborative filtering recommendation systems are much more common than content-based systems. This is primarily because they typically give better results. Some practitioners also find collaborative filtering recommendation systems easier to understand.
Collaborative filtering recommendation systems also have a unique feature that content-based systems are missing. Namely, they have the ability to learn features on their own.
This means that they can even start identifying similarities between items based on attributes that you haven’t even told them to consider.
There are two subcategories within collaborative filtering:
- Memory-based collaborative filtering
- Model-based collaborative filtering
You don’t need to know the differences between these two types of collaborative filtering recommendation systems to be successful in machine learning. It is enough to recognize that multiple types exist.
Section Wrap-up
Here is a brief summary of what we discussed about recommendation systems in this tutorial:
- Examples of recommendation systems in the real world
- The different types of recommendation systems, and how collaborative filtering systems are more commonly used than content-based recommendation systems
- The relationship between recommendation systems and linear algebra
Linear Regression
Linear regression is used to predict some y values based on the value of another set of x values.
The History of Linear Regression
Linear regression was created in the 1800s by Francis Galton.
Galton was a scientist studying the relationship between parents and children. More specifically, Galton was investigating the relationship between the heights of fathers and the heights of their sons.
Galton’s first discovery was that sons tended to be roughly as tall as their fathers. This is not surprising.
Later on, Galton discovered something much more interesting. The son’s height tended to be closer to the overall average height of all people than it was to his own father.
Galton gave this phenomenon a name: regression. Specifically, he said “A father’s son’s height tends to regress (or drift towards) the mean (average) height”.
This led to an entire field in statistics and machine learning called regression.
The Mathematics of Linear Regression
When creating a regression model, all that we are trying to do is draw a line that is as close as possible to each point in a data set.
The typical example of this is the “least squares method” of linear regression, which only calculates the closeness of a line in the up-and-down direction.
Here is an example to help illustrate this:
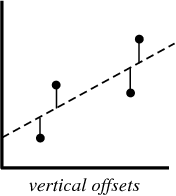
When you create a regression model, your end product is an equation that you can use to predict the y-value of an x-value, without actually knowing the y-value in advance.
Logistic Regression
Logistic regression is similar to linear regression except that instead of calculating a numerical y value, it estimates which category a data point belongs to.
What is Logistic Regression?
Logistic regression is a machine learning model that is used to solve classification problems.
Here are a few examples of machine learning classification problems:
- Spam emails (spam or not spam?)
- Car insurance claims (write-off or repair?)
- Disease diagnosis
Each of the classification problems have exactly two categories, which makes them examples of binary classification problems.
Logistic regression is well-suited for solving binary classification problems – we just assign the different categories a value of 0 and 1 respectively.
Why do we need logistic regression? Because you can’t use a linear regression model to make binary classification predictions. It wouldn't lead to a good fit, since you’re trying to fit a straight line through a dataset with only two possible values.
This image may help you understand why linear regression models are poorly suited for binary classification problems:
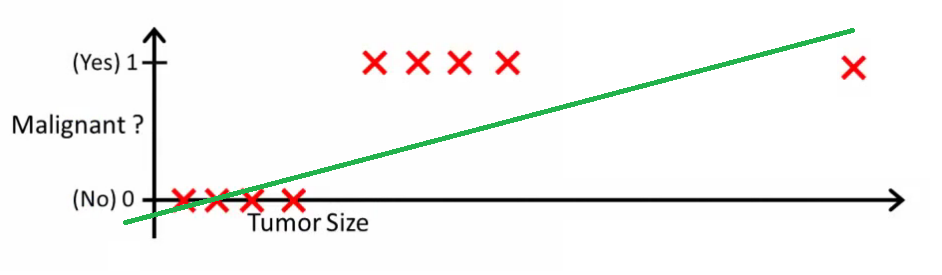
In this image, the y-axis represents the probability that a tumor is malignant. Conversely, the value 1-y represents the probability that a tumor is not malignant. As you can see, the linear regression model does a poor job of predicting this probability for most of the observations in the data set.
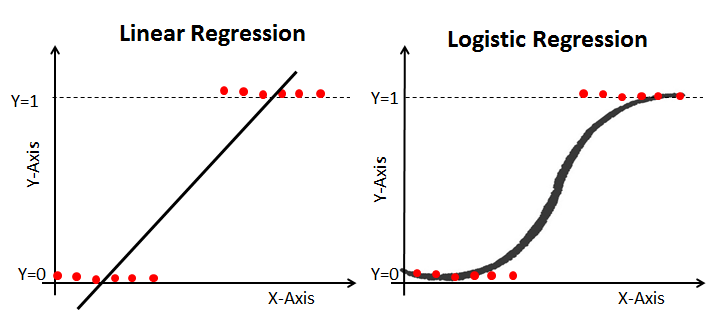
This is why logistic regression models are useful. They have a bend to their line of best fit, which makes them much better-suited for predicting categorical data.
Here is an example that compares a linear regression model to a logistic regression model using the same training data:
The Sigmoid Function
The reason why the logistic regression model has a bend in its curve is because it is not calculated using a linear equation. Instead, logistic regression models are built using the Sigmoid Function (also called the Logistic Function because of its use in logistic regression).
You will not have to memorize the Sigmoid Function to be successful in machine learning. With that said, having some understanding of its appearance is useful.
The equation is shown below:
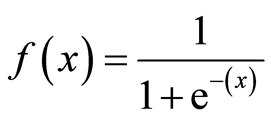
The main characteristic of the Sigmoid Function worth understanding is this: no matter what value you pass into it, it will always generate an output somewhere between 0 and 1.
Using Logistic Regression Models to Make Predictions
To use the linear regression model to make predictions, you generally need to specify a cutoff point. This cutoff point is typically 0.5.
Let’s use our cancer diagnosis example from our earlier image to see this principle in practice. If the logistic regression model outputs a value below 0.5, then the data point is categorized as a non-malignant tumor. Similarly, if the Sigmoid Function outputs a value above 0.5, then the tumor would be classified as malignant.
Using a Confusion Matrix to Measure Logistic Regression Performance
A confusion matrix can be used as a tool to compare true positives, true negatives, false positives, and false negatives in machine learning.
Confusion matrices are particularly useful when used to measure the performance of logistic regression models. Here is an example of how we could use a confusion matrix:
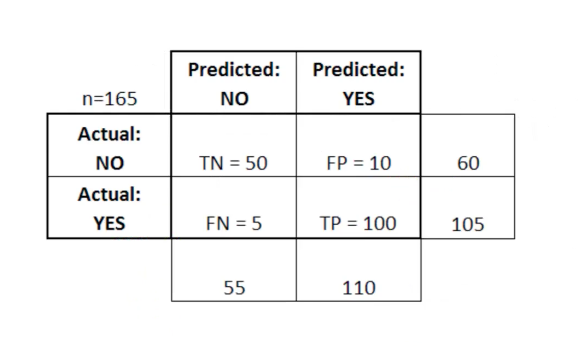
A confusion matrix is useful for assessing whether your model is particularly weak in a specific quadrant of the confusion matrix. As an example, it might have an abnormally high number of false positives.
It can also be helpful in certain applications, to make sure that your model performs well in an especially dangerous zone of the confusion matrix.
In this cancer example, for instance, you’d want to be very sure that you model does not have a very high rate of false negatives, as this would indicate that someone has a malignant tumor that you incorrectly classified as non-malignant.
Section Wrap-up
In this section, you had your first exposure to logistic regression machine learning models.
Here is a brief summary of what you learned about logistic regression:
- The types of classification problems that are suitable to be solved using logistic regression models
- That the logistic function (also called the Sigmoid Function) always outputs a value between 0 and 1
- How to use cutoff points to make predictions using a logistic regression machine learning model
- Why confusion matrices are useful to measure the performance of logistic regression models
K-Nearest Neighbors
The K-nearest neighbors algorithm can help you solve classification problems where there are more than two categories.
What is the K-Nearest Neighbors Algorithm?
The K-nearest neighbors algorithm is a classification algorithm that is based on a simple principle. In fact, the principle is so simple that it is best understood through example.
Imagine that you had data on the height and weight of football players and basketball players. The K-nearest neighbors algorithm can be used to predict whether a new athlete is either a football player or a basketball player.
To do this, the K-nearest neighbors algorithm identifies the K data points that are closest to the new observation.
The following image visualizes this, with a K value of 3:
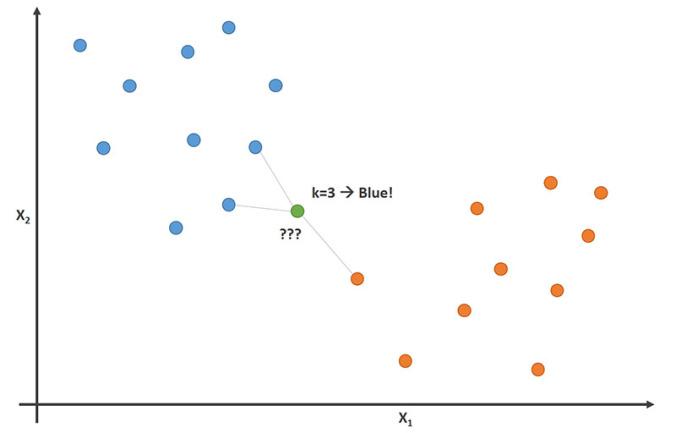
In this image, the football players are labeled as blue data points and the basketball players are labeled as orange dots. The data point that we are attempting to classify is labeled as green.
Since the majority (2 out of 3) of the closets data points to the new data points are blue football players, then the K-nearest neighbors algorithm will predict that the new data point is also a football player.
The Steps for Building a K-Nearest Neighbors Algorithm
The general steps for building a K-nearest neighbors algorithm are:
- Store all of the data
- Calculate the Euclidean distance from the new data point
xto all the other points in the data set - Sort the points in the data set in order of increasing distance from
x - Predict using the same category as the majority of the
Kclosest data points tox
The Importance of K in a K-Nearest Neighbors Algorithm
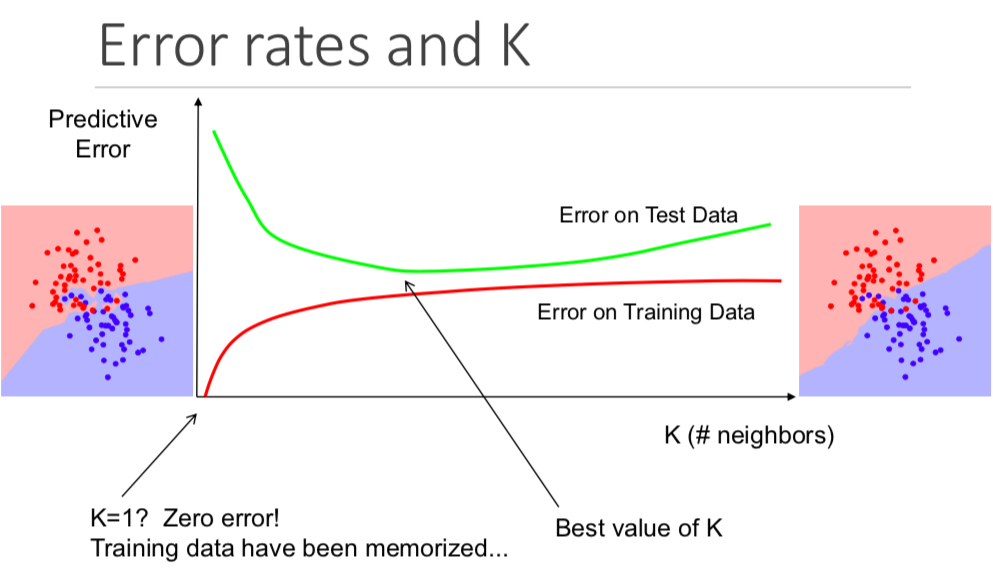
Although it might not be obvious from the start, changing the value of K in a K-nearest neighbors algorithm will change which category a new point is assigned to.
More specifically, having a very low K value will cause your model to perfectly predict your training data and poorly predict your test data. Similarly, having too high of a K value will make your model unnecessarily complex.
The following visualization does an excellent job of illustrating this:
The Pros and Cons of the K-Nearest Neighbors Algorithm
To conclude this introduction to the K-nearest neighbors algorithm, I wanted to briefly discuss some pros and cons of using this model.
Here are some main advantages to the K-nearest neighbors algorithm:
- The algorithm is simple and easy to understand
- It is trivial to train the model on new training data
- It works with any number of categories in a classification problem
- It is easy to add more data to the data set
- The model accepts only two parameters:
Kand the distance metric you’d like to use (usually Euclidean distance)
Similarly, here are a few of the algorithm’s main disadvantages:
- There is a high computational cost to making predictions, since you need to sort the entire data set
- It does not work well with categorical features
Section Wrap-up
Here is a brief summary of what you just learned about the k-nearest neighbors algorithm:
- An example of a classification problem (football players vs. basketball players) that the K-nearest neighbors algorithm could solve
- How the K-nearest neighbors uses the Euclidean distance of the neighboring data points to predict which category a new data point belongs to
- Why the value of
Kmatters for making predictions - The pros and cons of using the K-nearest neighbors algorithm
Decision Trees and Random Forests
Decision trees and randoms forests are both examples of tree methods.
More specifically, decision trees are machine learning models used to make predictions by cycling through every feature in a data set, one-by-one. Random forests are ensembles of decision trees that used random orders of the features in the data sets.
What Are Tree Methods?
Before we dig into the theoretical underpinnings of tree methods in machine learning, it is helpful to start with an example.
Imagine that you play basketball every Monday. Moreover, you always invite the same friend to come play with you.
Sometimes the friend actually comes. Sometimes they don't.
The decision on whether or not to come depends on numerous factors, like weather, temperature, wind, and fatigue. You start to notice these features and begin tracking them alongside your friend's decision whether to play or not.
You can use this data to predict whether or not your friend will show up to play basketball. One technique you could use is a decision tree. Here’s what this decision tree would look like:
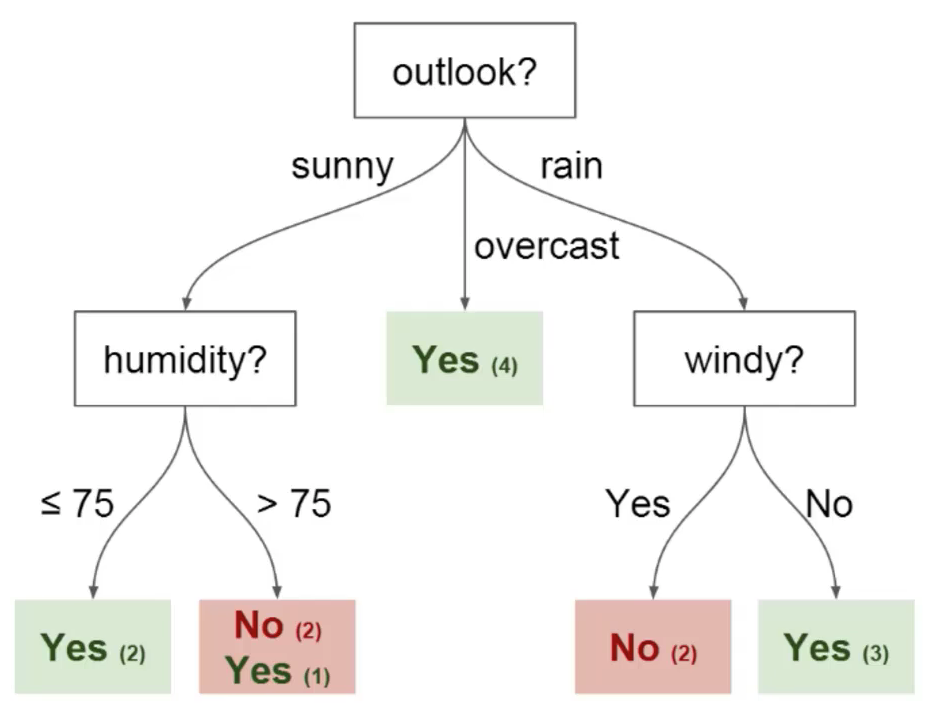
Every decision tree has two types of elements:
Nodes: locations where the tree splits according to the value of some attributeEdges: the outcome of a split to the next node
You can see in the image above that there are nodes for outlook, humidity and windy. There is an edge for each potential value of each of those attributes.
Here are two other pieces of decision tree terminology that you should understand before proceeding:
Root: the node that performs the first splitLeaves: terminal nodes that predict the final outcome
You now have a basic understanding of what decision trees are. We will learn about how to build decision trees from scratch in the next section.
How to Build Decision Trees From Scratch
Building decision trees is harder than you might imagine. This is because deciding which features to split your data on (which is a topic that belongs to the fields of Entropy and Information Gain) is a mathematically complex problem.
To address this, machine learning practitioners typically use many decision trees using a random sample of features chosen as the split.
Said differently, a new random sample of features is chosen for every single tree at every single split. This technique is called random forests.
In general, practitioners typically chose the size of the random sample of features (denoted m) to be the square root of the number of total features in the data set (denoted p). To be succinct, m is the square root of p, and then a specific feature is randomly selected from m.
If this does not make complete sense right now, do not worry. It will be more clear when you eventually build your first random forest model.
The Benefits of Using Random Forests
Imagine that you’re working with a data set that has one very strong feature. Said differently, the data set has one feature that is much more predictive of the final outcome than the other features in the data set.
If you’re building your decision trees manually, then it makes sense to use this feature as the top split of the decision tree. This means that you’ll have multiple trees whose predictions are highly correlated.
We want to avoid this since taking the average of highly correlated variables does not significantly reduce variance. By randomly selecting features for each tree in a random forest, the trees become decorrelated and the variance of the resulting model is reduced. This decorrelation is the main advantage of using random forests over handmade decision trees
Section Wrap-up
Here is a brief summary of what you learned about decision trees and random forests in this article:
- An example of a problem that you could predict using decision trees
- The elements of a decision tree:
nodes,edges,roots, andleaves - How taking random samples of decision tree features allows us to build a random forest
- Why using random forests to decorrelate variables can be helpful for reducing the variance of your final model
Support Vector Machines
Support vector machines are classification algorithms (although, technically speaking, they could also be used to solve regression problems) that divide a data set into categories based by slicing through the widest gap between categories. This concept will be made more clear through visualizations in a moment.
What Are Support Vector Machines?
Support vector machines – or SVMs for short – are supervised machine learning models with associated learning algorithms that analyze data and recognize patterns.
Support vector machines can be used for both classification problems and regression problems. In this article, we will specifically be looking at the use of support vector machines for solving classification problems.
How Do Support Vector Machines Work?
Let’s dig in to how support vector machines really work.
Given a set of training examples – each of which is marked for belonging to one of two categories – a support vector machine training algorithm builds a model. This model assigns new examples into one of the two categories. This makes the support vector machine a non-probabilistic binary linear classifier.
The SVM uses geometry to make categorical predictions.
More specifically, an SVM model maps the data points as points in space and divides the separate categories so that they are divided by an open gap that is as wide as possible. New data points are predicted to belong to a category based on which side of the gap they belong to.
Here is an example visualization that can help you understand the intuition behind support vector machines:

As you can see, if a new data point falls on the left side of the green line, it will be labeled with the red category. Similarly, if a new data point falls on the right side of the green line, it will get labelled as belonging to the blue category.
This green line is called a hyperplane, which is an important piece of vocabulary for support vector machine algorithms.
Let’s take a look at a different visual representation of a support vector machine:

In this diagram, the hyperplane is labelled as the optimal hyperplane. Support vector machine theory defines the optimal hyperplane as the one that maximizes the margin between the closest data points from each category.
As you can see, the margin line actually touches three data points – two from the red category and one from the blue category. These data points which touch the margin lines are called support vectors and are where support vector machines get their name from.
Section Wrap-up
Here is a brief summary of what you just learned about support vector machines:
- That support vector machines are an example of a supervised machine learning algorithm
- That support vector machines can be used to solve both classification and regression problems
- How support vector machines categorize data points using a hyperplane that maximizes the margin between categories in a data set
- That the data points that touch margin lines in a support vector machine are called support vectors. These data points are where support vector machines derive their name from.
K-Means Clustering
K-means clustering is a machine learning algorithm that allows you to identify segments of similar data within a data set.
What is K-Means Clustering?
K-means clustering is an unsupervised machine learning algorithm.
This means that it takes in unlabelled data and will attempt to group similar clusters of observations together within your data.
K-means clustering algorithms are highly useful for solving real-world problems. Here are a few use cases for this machine learning model:
- Customer segmentation for marketing teams
- Document classification
- Delivery route optimization for companies like Amazon, UPS, or FedEx
- Identifying and reacting to crime centers within a city
- Professional sport analytics
- Predicting and preventing cybercrime
The primary goal of a K means clustering algorithm is to divide a data set into distinct groups such that the observations within each group are similar to each other.
Here is a visual representation of what this looks like in practice:
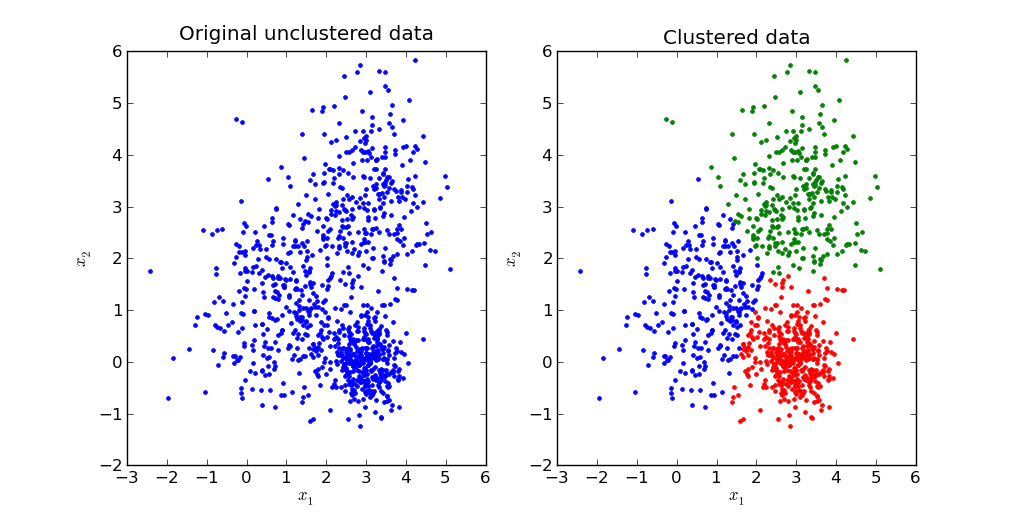
We will explore the mathematics behind a K-means clustering in the next section of this tutorial.
How Do K-Means Clustering Algorithms Work?
The first step in running a K-means clustering algorithm is to select the number of clusters you'd like to divide your data into. This number of clusters is the K value that is referenced in the algorithm’s name.
Choosing the K value within a K-means clustering algorithm is an important choice. We will talk more about how to chose a proper value of K later in this article.
Next, you must randomly assign each point in your data set to a random cluster. This gives our initial assignment which you then run the following iteration on until the clusters stop changing:
- Compute each cluster’s centroid by taking the mean vector of points within that cluster
- Re-assign each data point to the cluster that has the closest centroid
Here is an animation of how this works in practice for a K-means clustering algorithm with a K value of 3. You can see the centroid of each of cluster represented by a black + character.
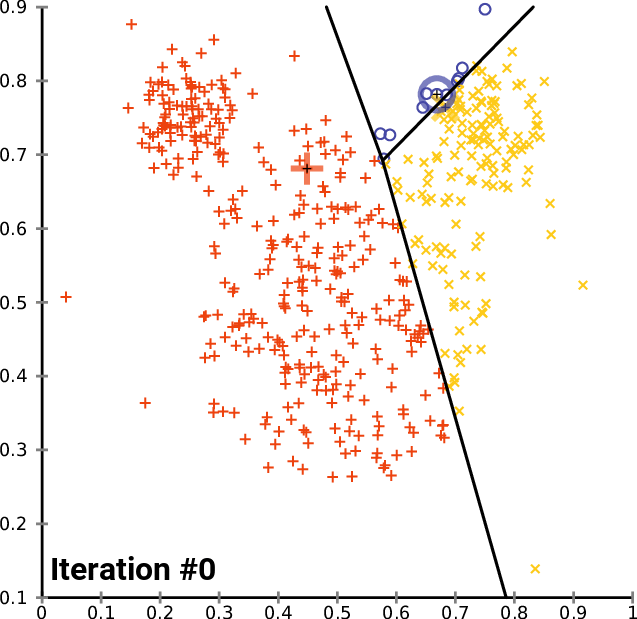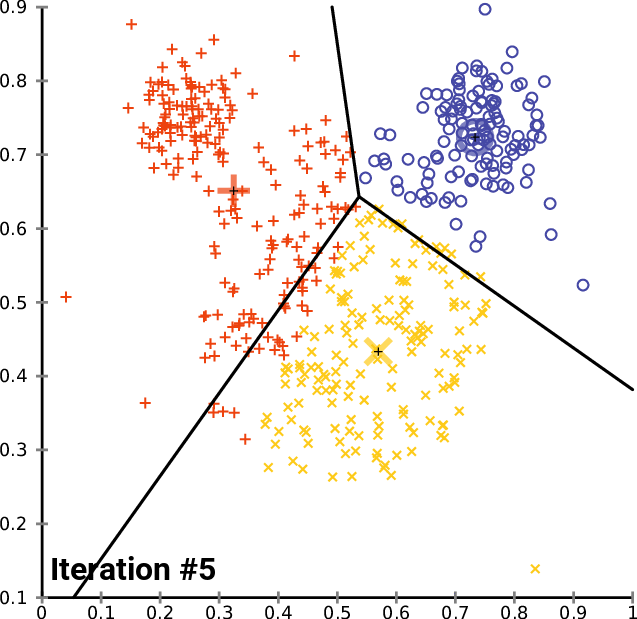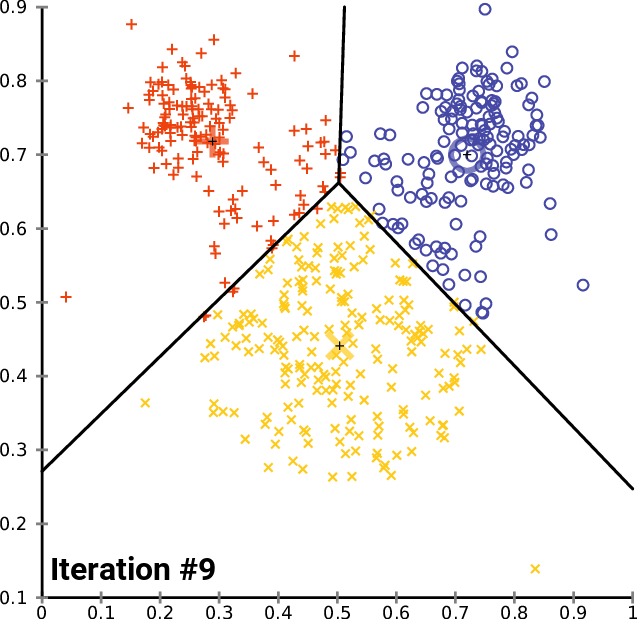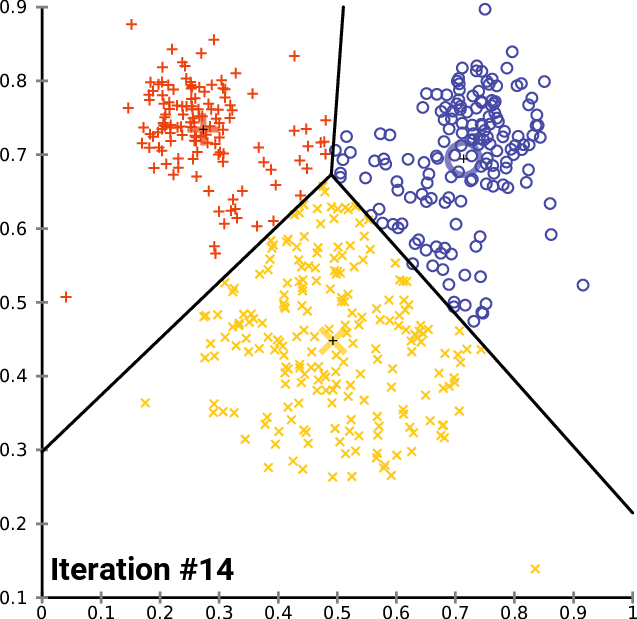
As you can see, this iteration continues until the clusters stop changing – meaning data points are no longer being assigned to new clusters.
Choosing A Proper K Value For K Means Clustering Algorithms
Choosing a proper K value for a K-means clustering algorithm is actually quite difficult. There is no “right” answer for choosing the “best” K value.
One method that machine learning practitioners often use is called the elbow method.
To use the elbow method, the first thing you need to do is compute the sum of squared errors (SSE) for you K-means clustering algorithm for a group of K values. SSE in a K means clustering algorithm is defined as the sum of the squared distance between each data point in a cluster and that cluster’s centroid.
As an example of this step, you might compute the SSE for K values of 2, 4, 6, 8, and 10.
Next, you will want to generate a plot of the SSE against these different K values. You will see that the error decreases as the K value increases.
This makes sense – the more categories you create within a data set, the more likely it is that each data point is close to the center of its specific cluster.
With that said, the idea behind the elbow method is to choose a value of K at which the SSE slows its rate of decline abruptly. This abrupt decrease produces an elbow in the graph.
As an example, here is a graph of SSE against K. In this case, the elbow method would suggest using a K value of approximately 6.
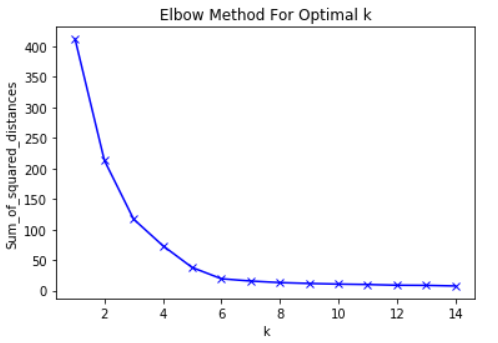
Importantly, 6 is just an estimate for a good value of K to use. There is never a “best” K value in a K-means clustering algorithm. As with many things in the field of machine learning, this is a highly situation-dependent decision.
Section Wrap-up
Here is a brief summary of what you learned in this article:
- Examples of unsupervised machine learning problems that the K-means clustering algorithm is capable of solving
- The basic principles of what a K-means clustering algorithm is
- How the K-means clustering algorithm works
- How to use the elbow method to select an appropriate value of
Kin a K-means clustering model
Principal Component Analysis
Principal component analysis is used to transform a many-featured data set into a transformed data set with fewer features where each new feature is a linear combination of the preexisting features. This transformed data set aims to explain most of the variance of the original data set with far more simplicity.
What is Principal Component Analysis?
Principal component analysis is a machine learning technique that is used to examine the interrelations between sets of variables.
Said differently, principal component analysis studies sets of variables in order to identify the underlying structure of those variables.
Principal component analysis is sometimes called factor analysis.
Based on this description, you might be think that principal component analysis is quite similar to linear regression.
That is not the case. In fact, these two techniques have some important differences.
The Differences Between Linear Regression and Principal Component Analysis
Linear regression determines a line of best fit through a data set. Principal component analysis determines several orthogonal lines of best fit for the data set.
If you’re unfamiliar with the term orthogonal, it just means that the lines are at right angles (90 degrees) to each other – like North, East, South, and West are on a map.
Let’s consider an example to help you understand this better.
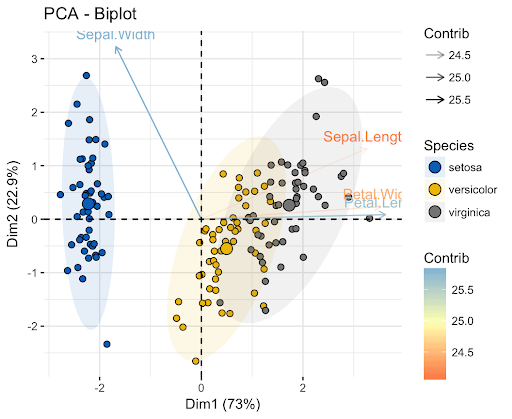
Take a look at the axis labels in this image.
In this image, the x-axis principal component examples 73% of the variance in the data set. The y-axis principal component explains about 23% of the variance in the data set.
This means that 4% of the variance in the data set remains unexplained. You could reduce this number further by adding more principal components to your analysis.
Section Wrap-up
Here’s a brief summary of what you learned about principal component analysis in this tutorial:
- That principal component analysis attempts to find orthogonal factors that determine the variability in a data set
- The differences between principal component analysis and linear regression
- What the orthogonal principal components look like when visualized inside of a data set
- That adding more principal components can help you to explain more of the variance in a data set

