Topic Modeling Tutorial – How to Use SVD and NMF in Python

In the context of Natural Language Processing (NLP), topic modeling is an unsupervised learning problem whose goal is to find abstract topics in a collection of documents.

Topic Modeling answers the question: "Given a text corpus of many documents, can we find the abstract topics that the text is talking about?"

In this tutorial, you’ll:

Learn about two powerful matrix factorization techniques - Singular Value Decomposition (SVD) and Non-negative Matrix Factorization (NMF)
Use them to find topics in a collection of documents

By the end of this tutorial, you'll be able to build your own topic models to find topics in any piece of text.📚📑

Let's get started.

What is Topic Modeling?
TF-IDF Score Equation
Topic Modeling Using Singular Value Decomposition (SVD)
What is Truncated SVD or k-SVD?
Topic Modeling Using Non-Negative Matrix Factorization (NMF)
7 Steps to Use SVD for Topic Modeling
How to Visualize Topics as Word Clouds
How to Use NMF for Topic Modeling
SVD vs NMF – An Overview of the Differences

What is Topic Modeling?

Let's start by understanding what topic modeling is.

Suppose you're given a large text corpus containing several documents. You'd like to know the key topics that reside in the given collection of documents without reading through each document.

Topic Modeling helps you distill the information in the large text corpus into a certain number of topics. Topics are groups of words that are similar in context and are indicative of the information in the collection of documents.

The general structure of the Document-Term Matrix for a text corpus containing M documents, and N terms in all, is shown below:

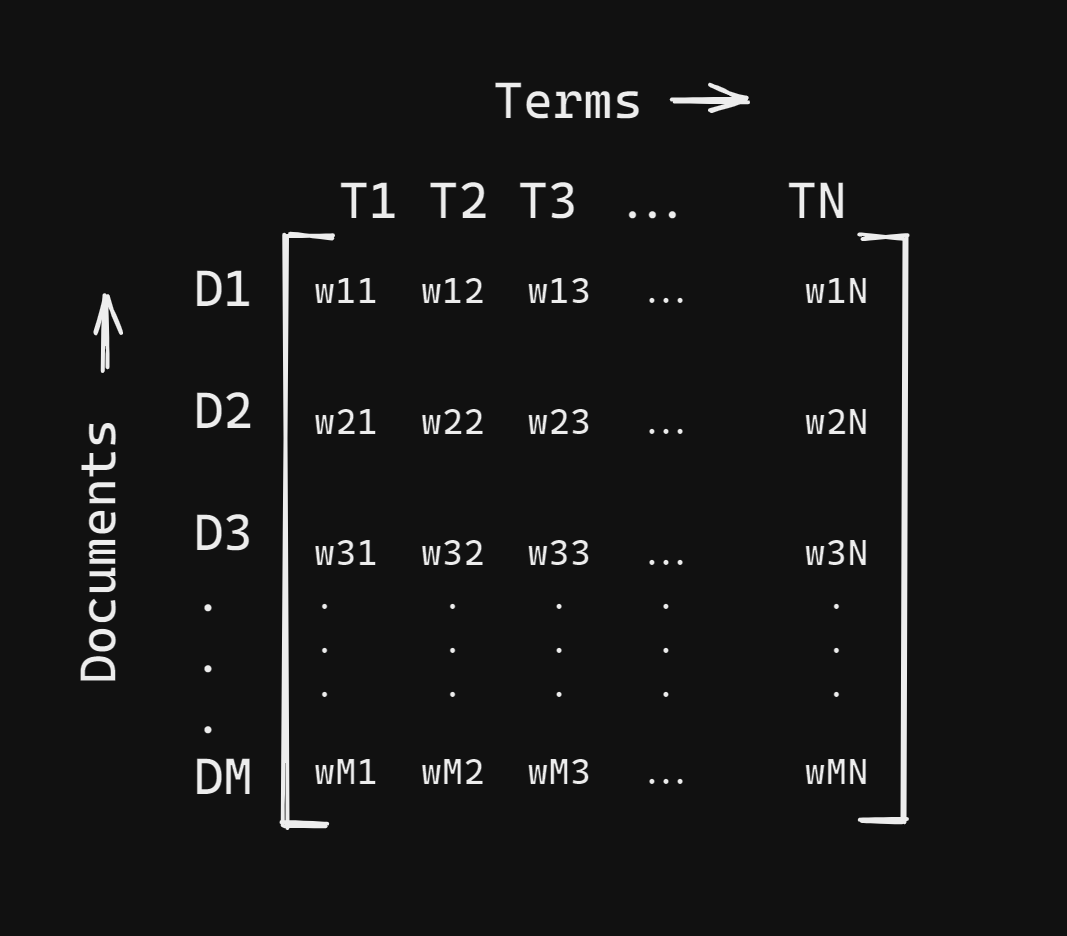
Let's parse the matrix representation:

D1, D2, ..., DM are the M documents.
T1, T2, ..., TN are the N terms

To populate the Document-Term Matrix, let’s use the widely-used metric—the TF-IDF Score.

TF-IDF Score Equation

The TF-IDF score is given by the following equation:

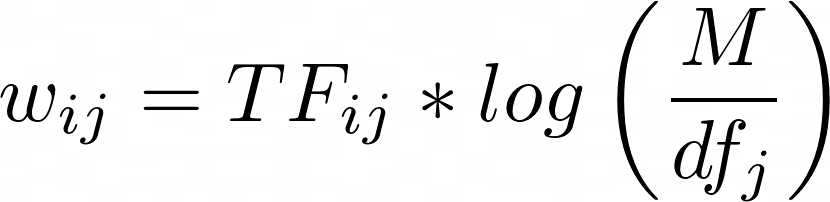
where,

TF_ij is the number of times the term Tj occurs in the document Di.
dfj is the number of documents containing the term Tj

A term that occurs frequently in a particular document, and rarely across the entire corpus has a higher IDF score.

I hope you’ve now gained a cursory understanding of the DTM and the TF-IDF score. Let’s now go over the matrix factorization techniques.

Topic Modeling Using Singular Value Decomposition (SVD)

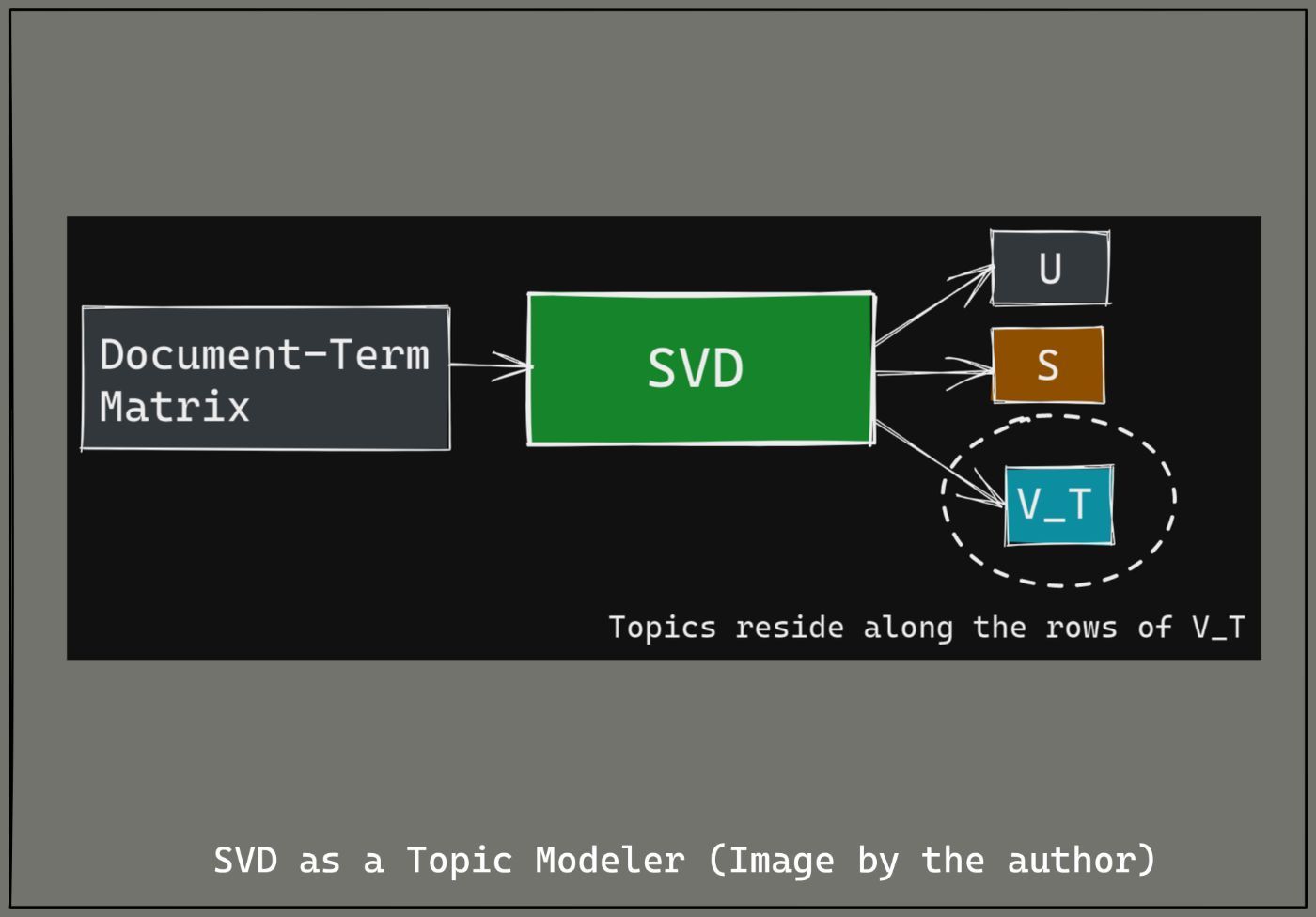
The use of Singular Value Decomposition (SVD) for topic modeling is explained in the figure below:

Singular Value Decomposition on the the Document-Term Matrix D gives the following three matrices:

The left singular vector matrix U. This matrix is obtained by the eigen decomposition of the Gram matrix D.D_T—also called the document similarity matrix. The i,j-th entry of the document similarity matrix signifies how similar document i is to document j.
The matrix of singular values S, which (values) signify the relative importance of topics.
The right singular vector matrix V_T, which is also called the term topic matrix. The topics in the text reside along the rows of this matrix.

If you'd like to refresh the concept of eigen decomposition, here's an excellent tutorial by Grant Sanderson from 3Blue1Brown. It explains eigenvectors and eigenvalues visually.

It's totally fine if you find the working of SVD a bit difficult to understand. 🙂 For now, you may think of SVD as a black box that operates on your Document-Term Matrix (DTM) and yields 3 matrices, U, S, and V_T. And the topics reside along the rows of the matrix V_T.

Note: SVD is also called Latent Semantic Indexing (LSI).

What is Truncated SVD or k-SVD?

Suppose you have a text corpus of 150 documents. Would you prefer skimming through 150 different topics that describe the corpus, or would you be happy reading through 10 topics that can convey the content of the corpus?

Well, it's often helpful to fix a small number of topics that best convey the content of the text. And this is what motivates k-SVD.

As matrix multiplication requires a lot of computation, it's preferred to choose the k largest singular values, and the topics corresponding to them. The working of k-SVD is illustrated below:

Topic Modeling Using Non-Negative Matrix Factorization (NMF)

Non-negative Matrix Factorization (NMF) works as shown below:

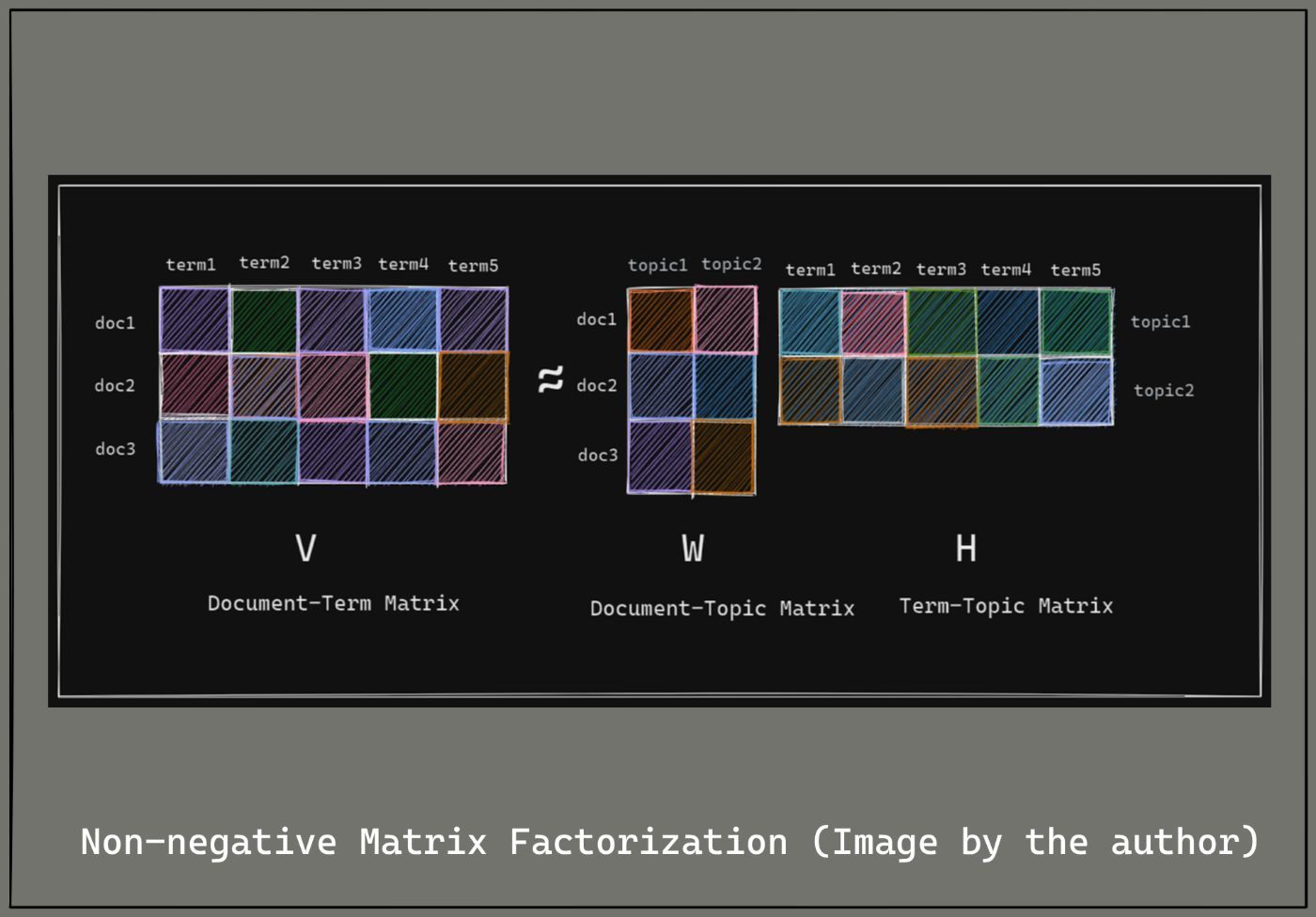
Non-negative Matrix Factorization acts on the Document-Term Matrix and yields the following:

The matrix W which is called the document-topic matrix. This matrix shows the distribution of the topics across the documents in the corpus.
The matrix H which is also called the term-topic matrix. This matrix captures the significance of terms across the topics.

NMF is easier to interpret as all the elements of the matrices W and H are now non-negative. So a higher score corresponds to greater relevance.

But how do we get matrices W and H?

NMF is a non-exact matrix factorization technique. This means that you cannot multiply W and H to get back the original document-term matrix V.

The matrices W and H are initialized randomly. And the algorithm is run iteratively until we find a W and H that minimize the cost function.

The cost function is the Frobenius norm of the matrix V - W.H, as shown below:

The Frobenius norm of a matrix A with m rows and n columns is given by the following equation:

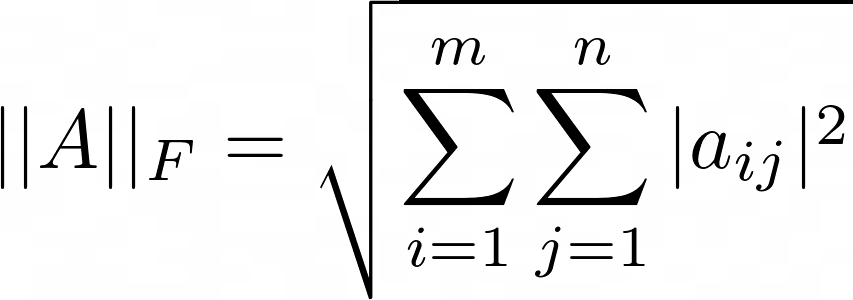
7 Steps to Use SVD for Topic Modeling

1️⃣ To use SVD to get topics, let's first get a text corpus. The following code cell contains a piece of text on computer programming.

text=["Computer programming is the process of designing and building an executable computer program to accomplish a specific computing result or to perform a specific task.",

      "Programming involves tasks such as: analysis, generating algorithms, profiling algorithms' accuracy and resource consumption, and the implementation of algorithms in a chosen programming language (commonly referred to as coding).",

      "The source program is written in one or more languages that are intelligible to programmers, rather than machine code, which is directly executed by the central processing unit.",

      "The purpose of programming is to find a sequence of instructions that will automate the performance of a task (which can be as complex as an operating system) on a computer, often for solving a given problem.",

      "Proficient programming thus often requires expertise in several different subjects, including knowledge of the application domain, specialized algorithms, and formal logic.",

      "Tasks accompanying and related to programming include: testing, debugging, source code maintenance, implementation of build systems, and management of derived artifacts, such as the machine code of computer programs.",

      "These might be considered part of the programming process, but often the term software development is used for this larger process with the term programming, implementation, or coding reserved for the actual writing of code.",

      "Software engineering combines engineering techniques with software development practices.",

    "Reverse engineering is a related process used by designers, analysts and programmers to understand and re-create/re-implement"]

The text for which you need to find topics is now ready.

2️⃣ The next step is to import the TfidfVectorizer class from scikit-learn's feature extraction module for text data:

from sklearn.feature_extraction.text import TfidfVectorizer

You'll use the TfidfVectorizer class to get the DTM populated with the TF-IDF scores for the text corpus.

3️⃣ To use Truncated SVD (k-SVD) discussed earlier, you need to import the TruncatedSVD class from scikit-learn's decomposition module:

from sklearn.decomposition import TruncatedSVD

▶ Now that you've imported all the necessary modules, it's time to start your quest for topics in the text.

4️⃣ In this step, you'll instantiate a Tfidfvectorizer object. Let's call it vectorizer.

vectorizer = TfidfVectorizer(stop_words='english',smooth_idf=True) 
# under the hood - lowercasing,removing special chars,removing stop words
input_matrix = vectorizer.fit_transform(text).todense()

So far, you've:

☑ collected the text,
☑ imported the necessary modules, and
☑ obtained the input DTM.

Now you'll proceed with using SVD to obtain topics.

5️⃣ You'll now use the TruncatedSVD class that you imported in step 3️⃣.

svd_modeling= TruncatedSVD(n_components=4, algorithm='randomized', n_iter=100, random_state=122)
svd_modeling.fit(input_matrix)
components=svd_modeling.components_
vocab = vectorizer.get_feature_names()

6️⃣ Let’s write a function that gets the topics for us.

topic_word_list = []
def get_topics(components): 
  for i, comp in enumerate(components):
    terms_comp = zip(vocab,comp)
  sorted_terms = sorted(terms_comp, key= lambda x:x[1], reverse=True)[:7]
     topic=" "
     for t in sorted_terms:
      topic= topic + ' ' + t[0]
     topic_word_list.append(topic)
     print(topic_word_list)
  return topic_word_list
get_topics(components)

7️⃣ And it's time to view the topics, and see if they make sense. When you call the get_topics() function with the components obtained from SVD as the argument, you'll get a list of topics, and the top words in each of those topics.

Topic 1: 
  code programming process software term computer engineering

Topic 2: 
  engineering software development combines practices techniques used

Topic 3: 
  code machine source central directly executed intelligible

Topic 4: 
  computer specific task automate complex given instructions

And you have your topics in just 7 steps. Do the topics look good?

How to Visualize Topics as Word Clouds

In the previous section, you printed out the topics, and made sense of the topics using the top words in each topic.

Another popular visualization method for topics is the word cloud. In a word cloud, the terms in a particular topic are displayed in terms of their relative significance. The most important word has the largest font size, and so on.

!pip install wordcloud
from wordcloud import WordCloud
import matplotlib.pyplot as plt
for i in range(4):
  wc = WordCloud(width=1000, height=600, margin=3,  prefer_horizontal=0.7,scale=1,background_color='black', relative_scaling=0).generate(topic_word_list[i])
  plt.imshow(wc)
  plt.title(f"Topic{i+1}")
  plt.axis("off")
  plt.show()

The word clouds for topics 1 through 4 are shown in the image grid below:

As you can see, the font-size of words indicate their relative importance in a topic. These word clouds are also called topic clouds.

How to Use NMF for Topic Modeling

In this section, you'll run through the same steps as in SVD. You need to first import the NMF class from scikit-learn's decomposition module.

from sklearn.decomposition import NMF
NMF_model = NMF(n_components=4, random_state=1)
W = NMF_model.fit_transform(input_matrix)
H = NMF_model.components_

And then you may call the get_topics() function on the matrix H to get the topics.

Topic 1: 
  code machine source central directly executed intelligible

Topic 2: 
  engineering software process development used term combines

Topic 3: 
  algorithms programming application different domain expertise formal

Topic 4: 
  computer specific task programming automate complex given

For the given piece of text, you can see that both SVD and NMF give similar topic clouds.

SVD vs NMF – An Overview of the Differences

Now, let's put together the differences between these two matrix factorization techniques for topic modeling.

SVD is an exact matrix factorization technique – you can reconstruct the input DTM from the resultant matrices.
If you choose to use k-SVD, it's the best possible k-rank approximation to the input DTM.
Though NMF is a non-exact approximation to the input DTM, it's known to capture more diverse topics than SVD.

Wrapping Up

I hope you enjoyed this tutorial. As a next step, you may spin up your own Colab notebook using the code cells from this tutorial. You only have to plug in the piece of text that you'd like to find topics for, and you'd have your topics and word clouds ready!

Thank you for reading, and happy coding!

References and Further Reading on Topic Modeling

A Code-First Approach to Natural Language Processing by fast.ai
Computational Linear Algebra by fast.ai

Cover Image: Photo by Brett Jordan on Unsplash

Table of Contents