by Thalles Silva
An introduction to high-dimensional hyper-parameter tuning
Best practices for optimizing ML models

If you ever struggled with tuning Machine Learning (ML) models, you are reading the right piece.
Hyper-parameter tuning refers to the problem of finding an optimal set of parameter values for a learning algorithm.
Usually, the process of choosing these values is a time-consuming task.
Even for simple algorithms like Linear Regression, finding the best set for the hyper-parameters can be tough. With Deep Learning, things get even worse.
Some of the parameters to tune when optimizing neural nets (NNs) include:
- learning rate
- momentum
- regularization
- dropout probability
- batch normalization
In this short piece, we talk about the best practices for optimizing ML models. These practices come in hand mainly when the number of parameters to tune exceeds two or three.
The problem with Grid Search
Grid Search is usually a good choice when we have a small number of parameters to optimize. For two or even three different parameters, it might be the way to go.
For each hyper-parameter, we define a set of candidate values to explore.
Then, the idea is to exhaustively try every possible combination of the values of the individual parameters.
For each combination, we train and evaluate a different model.
In the end, we keep the one with the smallest generalization error.
The main problem with Grid Search is that it is an exponential time algorithm. Its cost grows exponentially with the number of parameters.
In other words, if we need to optimize p parameters and each one takes at most v values, it runs in O(vᵖ) time.
Also, Grid Search is not as effective in exploring the hyper-parameter space as we may think.
Take a look at the code above again. Using this setup, we are going to train a total of 256 different models. Note that if we decide to add one more parameter, the number of experiments would increase to 1024.
However, this setup only explores four different values for each hyper-parameter. That is it, we train 256 models to only explore four values of the learning rate, regularization, and so on.
Besides, Grid Search usually requires repetitive trials. Take the learning_rate_search values from the code above as an example.
learning_rate_search = [0.1, 0.01, 0.001, 0.0001]Suppose that after our first run (256 model trials), we get the best model with a learning rate value of 0.01.
In this situation, we should try to refine our search values by “zooming in” on the grid around 0.01 in the hope to find an even better value.
To do this, we could setup a new Grid Search and redefine the learning rate search range such as:
learning_rate_search = [0.006, 0.008, 0.01, 0.04, 0.06]But what if we get the best model with a learning rate value was 0.0001?
Since this value is at the very edge of our initial search range, we should shift the values and try again with a different set like:
learning_rate_search = [0.0001, 0.00006, 0.00002]And possibly try to refine the range after finding a good candidate.
All these details only emphasize how time-consuming hyper-parameter search can be.
A better approach — Random Search
How about choosing our hyper-parameter candidate values at random? As not intuitive as it might seem, this idea is almost always better than Grid Search.
A little bit of intuition
Note that some of the hyper-parameters are more important than others.
The learning rate and the momentum factor, for example, are more worth tuning than all others.
However, with the above exception, it is hard to know which ones play major roles in the optimization process. In fact, I would argue that the importance of each parameter might change for different model architectures and datasets.
Suppose we are optimizing over two hyper-parameters — the learning rate and the regularization strength. Also, take into consideration that only the learning rate matters for the problem.
In the case of Grid Search, we are going to run nine different experiments, but only try three candidates for the learning rate.
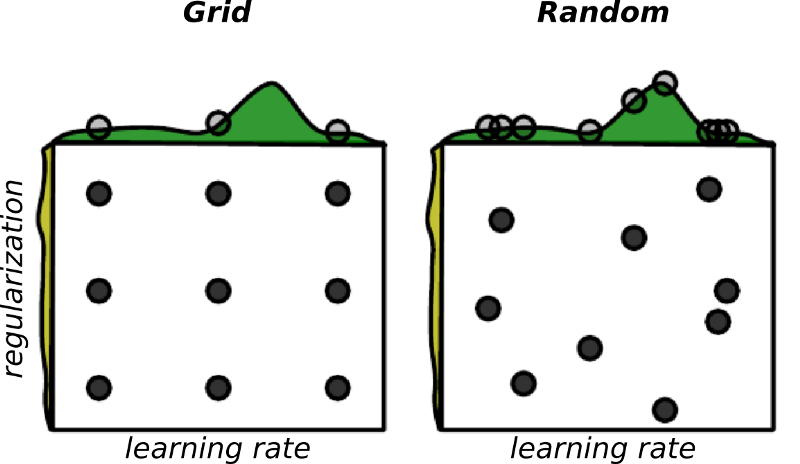
Now, take a look at what happens if we sample the candidates uniformly at random. In this scenario, we are actually exploring nine different values for each parameter.
If you are not yet convinced, suppose we are optimizing over three hyper-parameters. For example, the learning rate, the regularization strength, and momentum.

For Grid Search, we would be running 125 training runs, but only exploring five different values of each parameter.
On the other hand, with Random Search, we would be exploring 125 different values of each.
How to do it
If we want to try values for the learning rate, say within the range of 0.1 to 0.0001, we do:
Note that we are sampling values from a uniform distribution on a log scale.
You can think of the values -1 and -4 (for the learning rate) as the exponents in the interval [10e-1, 10e-4].
If we do not use a log-scale, the sampling will not be uniform within the given range. In other words, you should not attempt to sample values like:
In this situation, most of the values would not be sampled from a ‘valid’ region. Actually, considering the learning rate samples in this example, 72% of the values would fall in the interval [0.02, 0.1].
Moreover, 88% in the sampled values would come from the interval [0.01, 0.1]. That is, only 12% of the learning rate candidates, 3 values, would be sampled from the interval [0.0004, 0.01]. Do not do that.
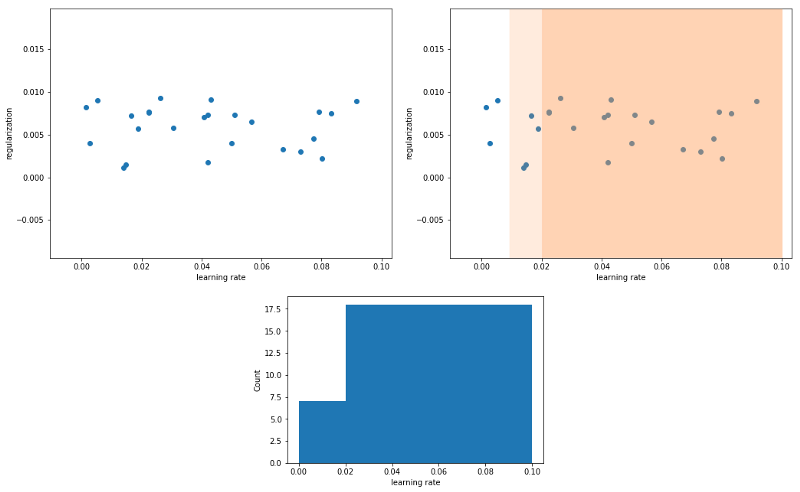
In the graphic below, we are sampling 25 random values from the range [0.1,0.0004]. The plot in the top left shows the original values.
In the top right, notice that 72% of the sampled values are in the interval [0.02, 0.1]. 88% of the values lie within the range [0.01, 0.1].
The bottom plot shows the distribution of values. Only 12% of the values are in the interval [0.0004, 0.01]. To solve this problem, sample the values from a uniform distribution in a log-scale.
A similar behavior would happen with the regularization parameter.
Also, note that like with Grid Search, you need to consider the two cases we mentioned above.
If the best candidate falls very near the edge, your range might be off and should be shifted and re-sampled. Also, after choosing the first good candidates, try re-sampling to a finer range of values.
In conclusion, these are the key takeaways.
- If you have more than two or three hyper-parameters to tune, prefer Random Search. It is faster/easier to implement and converges faster than Grid Search.
- Use an appropriate scale to pick your values. Sample from a uniform distribution in a log-space. This will allow you to sample values equally distributed across the parameters ranges.
- Regardless of Random or Grid Search, pay attention to the candidates you choose. Make sure the parameter’s ranges are properly set and refine the best candidates if possible.
Thanks for reading! For more cool stuff on Deep Learning, check out some of my previous articles:
How to train your own FaceID ConvNet using TensorFlow Eager execution
Faces are everywhere — from photos and videos on social media websites, to consumer security applications like the…medium.freecodecamp.orgMachine Learning 101: An Intuitive Introduction to Gradient Descent
Gradient descent is, with no doubt, the heart and soul of most Machine Learning (ML) algorithms. I definitely believe…towardsdatascience.com