What is an AVL Tree?
An AVL tree is a type of binary search tree. Named after it's inventors Adelson, Velskii, and Landis, AVL trees have the property of dynamic self-balancing in addition to all the other properties exhibited by binary search trees.
A BST is a data structure composed of nodes. It has the following guarantees:
- Each tree has a root node (at the top)
- The root node has zero, one, or two child nodes
- Each child node has zero, one, or two child nodes
- Each node has up to two children
- For each node, its left descendants are less than the current node, which is less than the right descendants
AVL trees have an additional guarantee:
- The difference between the depth of right and left sub-trees cannot be more than one. This difference is called the balance factor.
In order to maintain this guarantee, an implementation of an AVL will include an algorithm to rebalance the tree when adding an additional element would upset this guarantee
AVL trees have a worst case lookup, insert, and delete time of O(log n), where n is the number of nodes in the tree. The worst case space complexity is O(n).
AVL Insertion Process
Insertion in an AVL tree is similar to insertion in a binary search tree. But after inserting and element, you need to fix the AVL properties using left or right rotations:
- If there is an imbalance in the left child's right sub-tree, perform a left-right rotation
- If there is an imbalance in the left child's left sub-tree, perform a right rotation
- If there is an imbalance in the right child's right sub-tree, perform a left rotation
- If there is an imbalance in the right child's left sub-tree, perform a right-left rotation
AVL Tree Rotations
In AVL trees, after each operation like insertion and deletion, the balance factor of every node needs to be checked. If every node satisfies the balance factor condition, then the operation can be concluded. Otherwise, the tree needs to be rebalanced using rotation operations.
There are four rotations and they are classified into two types:
Left Rotation (LL Rotation)
In left rotations, every node moves one position to left from the current position.
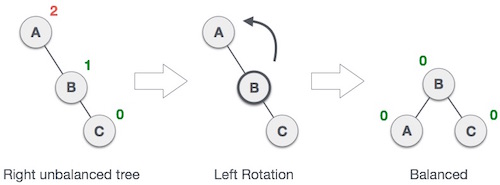
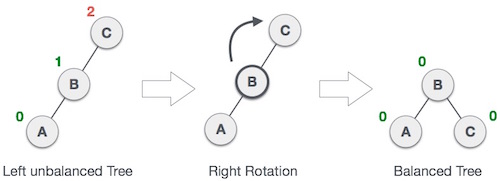
Right Rotation (RR Rotation)
In right rotations, every node moves one position to right from the current position.
Left-Right Rotation (LR Rotation)
Left-right rotations are a combination of a single left rotation followed by a single right rotation.
First, every node moves one position to the left, then one position to the right from the current position.
Right-Left Rotation (RL Rotation)
Right-left rotations are a combination of a single right rotation followed by a single left rotation.
First, every node moves one position to the right then, then one position to the left from the current position.
Application of AVL Trees
AVL trees are beneficial in cases like a database where insertions and deletions are not that frequent, but you frequently check for entries.
