Welcome
In this article, you will learn how the Binary Search algorithm works behind the scenes and how you can implement it in Python.
In particular, you will learn:
- How the algorithm works behind the scenes to find a target element.
- How its Python implementation works line by line.
- Why it is a very efficient algorithm compared to Linear Search.
- Its advantages and requirements.
Let's begin! ✨
🔹 Intro to Binary Search
This algorithm is used to find an element in an ordered sequence (for example: a list, tuple, or string).
Requirements
To apply the Binary Search algorithm to a sequence, the sequence already has to be sorted in ascending order. Otherwise, the algorithm will not find the correct answer. If it does, it will be by pure coincidence.
💡 Tip: You can sort the sequence before applying Binary Search with a sorting algorithm that meets your needs.
Input and Output
The algorithm (implemented as a function) needs this data:
- An ordered sequence of elements (for example: list, tuple, string).
- The target element that we are searching for.
It returns the index of the element that you are looking for if it's found. If the element is not found, -1 is returned.
Efficiency
It is very efficient compared to Linear Search (searching for an element one by one, starting from the first one) because we are able to "discard" half of the list on every step.
Let's start diving into this algorithm.
🔸 Visual Walkthrough
We will apply the Binary Search algorithm to this list:

💡 Tip: Notice that the list is already sorted. It included the indices as a visual reference.
Goal
We want to find the index of the integer 67.
Interval
Let's pretend that we are the algorithm. How do we start the process?
We start by selecting the two bounds of the interval where we want to search. We want to search the entire list, so we select index 0 as the lower bound and index 5 as the upper bound:
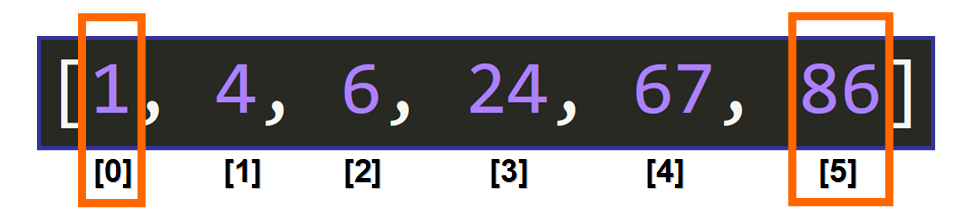
Middle Element
Now we need to find the index of the middle element in this interval. We do this by adding the lower bound and the upper bound and dividing the result by 2 using integer division.
In this case, (0 + 5)//2 is 2 because the result of 5/2 is 2.5 and integer division truncates the decimal part.
So the middle element is located at index 2, and the middle element is the number 6:
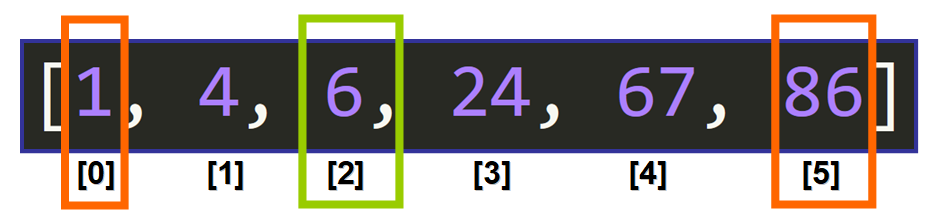
Comparisons
Now we need to start comparing the middle element with our target element to see what we need to do next.
We ask:
Is the middle element equal to the element that we are looking for?
6 == 67 # FalseNo, it isn't.
So we ask:
Is the middle element greater than the element that we are looking for?
6 > 67 # FalseNo, it isn't.
So the middle element is smaller than the element that we are looking for.
6 < 67 # TrueDiscard Elements
Since the list is already sorted, this tells us something extremely important. It tells us that we can "discard" the lower half of the list because we know that all the elements that come before the middle element will be smaller than the element that we are looking for, so our target element is not there.
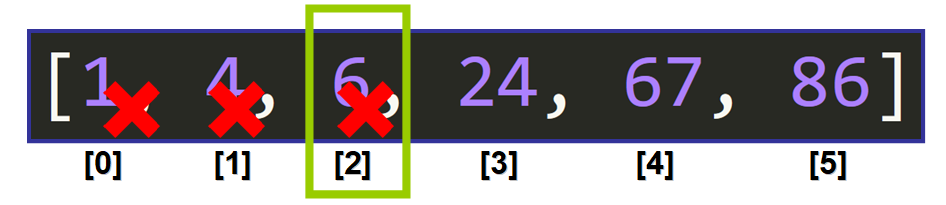
Start Again - Choose the Bounds
What do we do next? We've discarded the elements and the cycle is repeated again.
We have to choose the bounds for the new interval (see below). But notice that the upper bound is kept intact and only the lower bound is changed.
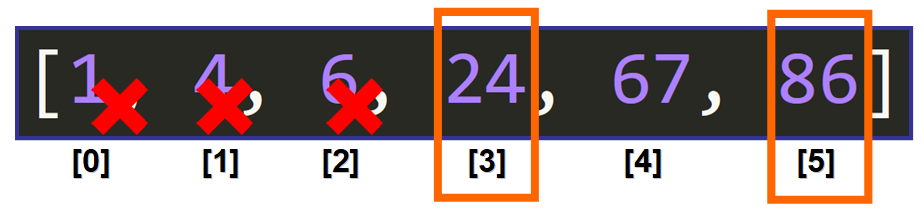
This is because the element that we are looking could be in the upper half of the list. The upper bound is kept intact and the lower bound is changed to "shrink" the interval to an interval where our target element could be found.
💡 Tip: If the middle element had been greater than the element that we are looking for, the upper bound would have been changed and the lower bound would have been kept intact. This way, we would discard the upper half of the list and continue searching in the lower half.
Middle Element
Now we need to find the index of the middle element by adding the lower bound to the upper bound and dividing the result by 2 using integer division.
The result of (3+5)//2 is 4, so the middle element is located at index 4 and the middle element is 67.
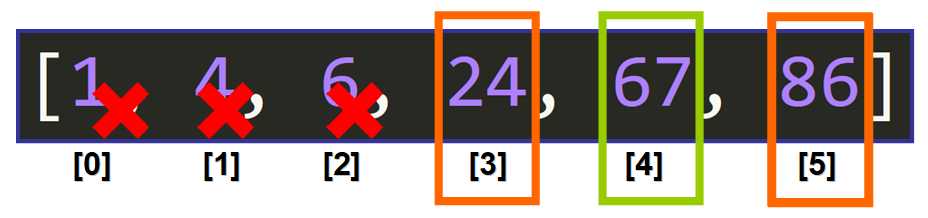
Comparisons
We ask:
Is the middle element equal to the element that we are looking for?
67 == 67 # TrueYes, it is! So we've found the element at index 4. The value 4 is returned and the algorithm was completed successfully.
💡 Tip: If the element had not been found, the process would have continued until the interval was no longer valid. If the element had not been found in the entire list, -1 would have been returned.
🔹 Code Walkthrough
Now that you have a visual intuition of how the algorithm works behind the scenes, let's dive into the iterative Python implementation by analyzing it line by line:
def binary_search(data, elem):
low = 0
high = len(data) - 1
while low <= high:
middle = (low + high)//2
if data[middle] == elem:
return middle
elif data[middle] > elem:
high = middle - 1
else:
low = middle + 1
return -1Header
Here we have the function header:
def binary_search(data, elem):It takes two arguments:
- The ordered sequence of elements (for example: list, tuple, or string).
- The element that we want to find.
Initial Interval
The next line sets the initial lower and upper bounds:
low = 0
high = len(data) - 1The initial lower bound is index 0 and the initial upper bound is the last index of the sequence.
Loop
We will repeat the process while there is a valid interval, while the lower bound is smaller than or equal to the upper bound.
while low <= high:💡 Tip: Remember that the bounds are indices.
Middle Element
On every iteration, we need to find the index of the middle element. To do this, we add the lower and upper bounds and divide the result by 2 using integer division.
middle = (low + high)//2💡 Tip: We use integer division in case the list or interval contains an even number of elements. For example, if the list had 6 elements and we did not use integer division, middle would be the result of (0 + 5)/2 which is 2.5. An index cannot be a float, so we truncate the decimal portion by using // and select the element at index 2.
Comparisons
With these conditionals (see below), we determine what to do depending on the value of the middle element data[middle]. We compare it to the target element that we are looking for.
if data[middle] == elem:
return middle
elif data[middle] > elem:
high = middle - 1
else:
low = middle + 1There are three options:
- If the middle element is equal to the element that we are looking for, we return the index immediately because we found the element.
if data[middle] == elem:
return middle- If the middle element is greater than the element that we are looking for, we reassign the upper bound because we know that the target element is in the lower half of the list.
elif data[middle] > elem:
high = middle - 1- Else, the only option left is that the middle element is smaller than the element that we are looking for, so we reassign the lower bound because we know that the target element is in the upper half of the list.
else:
low = middle + 1Element Not Found
If the loop is completed without finding the element, the value -1 is returned.
return -1and we have the final implementation of the Binary Search algorithm:
def binary_search(data, elem):
low = 0
high = len(data) - 1
while low <= high:
middle = (low + high)//2
if data[middle] == elem:
return middle
elif data[middle] > elem:
high = middle - 1
else:
low = middle + 1
return -1🔸 Special Cases
These are some particular cases that you may find as you start working with this algorithm:
Repeated Elements
If the element that you are looking for is repeated in the sequence, the index returned will depend on the number of elements and on the sequence of operations that the algorithm performs on the sequence.
>>> >>> b = [2, 2, 3, 6, 7, 7]
>>> binary_search(b, 7)
4
Element Not Found
If the element is not found, -1 is returned.
>>> b = [2, 2, 3, 6, 7, 7]
>>> binary_search(b, 8)
-1Empty Sequence
If the sequence is empty, -1 will be returned.
>>> b = []
>>> binary_search(b, 8)
-1Unsorted Sequence
If the sequence is unsorted, the answer will not be correct. Getting the correct index is pure coincidence and it could be due to the order of the elements in the sequence and the sequence of operations performed by the algorithm.
This example returns the correct result:
>>> b = [5, 7, 3, 0, -9, 2, 6]
>>> binary_search(b, 6)
6But this one doesn't:
>>> b = [5, 7, 3, 0, -9, 2, 10, 6]
>>> binary_search(b, 6)
-1💡 Tip: Think about why the first example returns the correct result. Hint: It's pure coincidence that the order of the elements happens to make the algorithm reach the correct index, but the step-by-step process evaluates 0, then 2, and finally 6. In this particular case, for this particular element, the correct index is found even if the sequence is not sorted.
🔹 A More Complex Example
Now that you're more familiar with the algorithm and its Python implementation, here we have a more complex example:
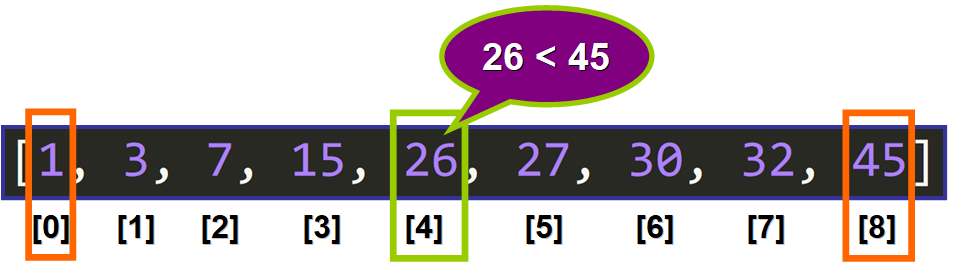
We want to find the index of the element 45 in this list using Binary Search:

First Iteration
The lower and upper bounds are selected:

The middle element (26) is selected:

But the middle element (26) is not the element that we are looking for, it is smaller than 45:
Second Iteration
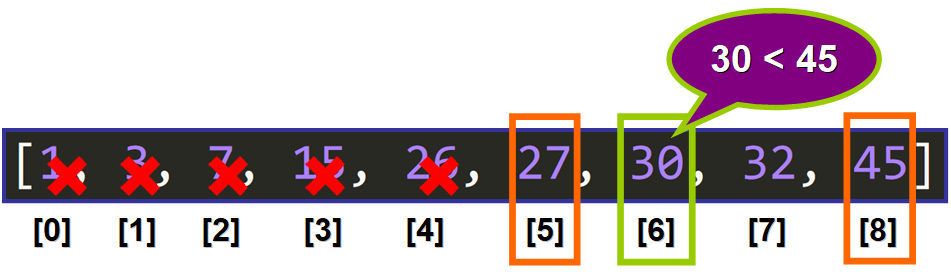
So we can discard all the elements that are smaller than the middle element and select new bounds. The new lower bound (27) is the element located immediately to the right of the previous middle element:

💡 Tip: Remember that the list is already sorted.
The new middle element (30) is selected:

The middle element (30) is not the element that we are looking for, it is smaller than 45:
Third Iteration
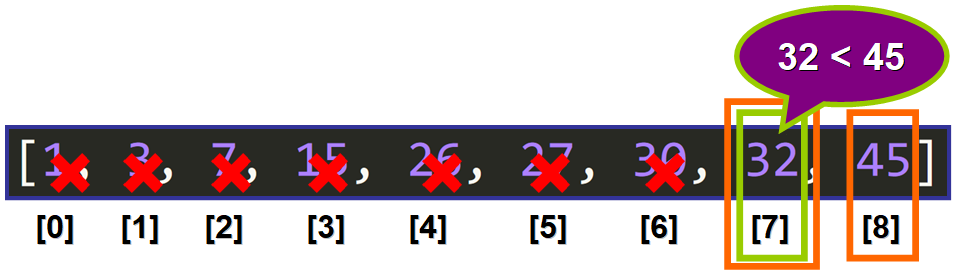
We can discard the elements that are smaller than or equal to 30 that have not been discarded already. The lower bound is updated to 32:

Here we have an interesting case: the middle element is one of the bounds of the current interval because (7+8)//2 is 7.

The middle element (32) is not the element that we are looking for (45), it is smaller.
Fourth Iteration
We can discard the elements that are smaller than or equal to 32 that have not been discarded already.
Here we have another very interesting case: the interval only has one element.

💡 Tip: This interval is valid because we wrote this condition while high <= low: , which includes intervals where the index of the lower bound is equal to the index of the upper bound.
The middle element is the only element in the interval because (8+8)//2 is 8, so the index of the middle element is 8 and the middle element is 45.
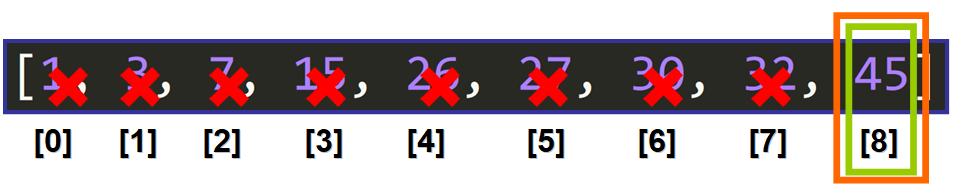
Now the middle element is the element that we are looking for, 45:
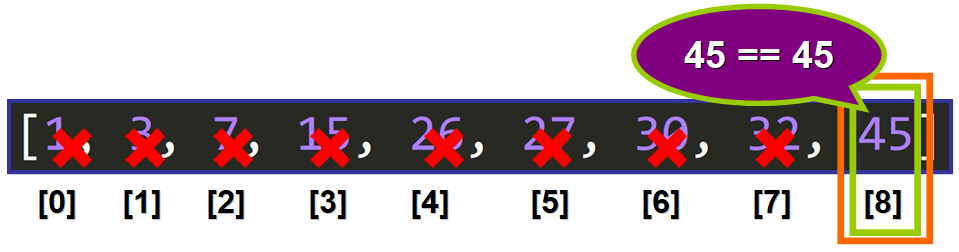
So the value 8 (the index) is returned:
>>> binary_search([1, 3, 7, 15, 26, 27, 30, 32, 45], 45)
8🔸 Extra Practice
If you would like to have some extra practice with this algorithm, try to explain how the algorithm works behind the scenes when it's applied to this list to find the integer 90:
[5, 8, 15, 26, 38, 56]- What happens step by step?
- What value is returned?
- Is the element found?
I really hope you liked my article and found it helpful. Now you can implement the Binary Search algorithm in Python. Check out my online course "Python Searching & Sorting Algorithms: A Practical Approach". Follow me on Twitter. ⭐️

